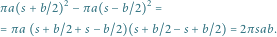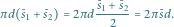O obrotach figur płaskich
W 1641 roku ukazały się Centrobaryca Paula Guldina, a w nich twierdzenie znane dziś jako reguły Guldina...
Oto ono
Twierdzenie. Jeśli figurę płaską 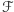 o polu
o polu 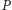 i obwodzie
i obwodzie 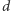 będziemy obracali wokół osi niemającej punktów wspólnych z wnętrzem
będziemy obracali wokół osi niemającej punktów wspólnych z wnętrzem 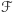 i leżącej w tej samej co ona płaszczyźnie, to powstała bryła będzie miała objętość
i leżącej w tej samej co ona płaszczyźnie, to powstała bryła będzie miała objętość 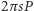 i pole powierzchni
i pole powierzchni 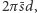 gdzie
gdzie  i
i  to, odpowiednio, odległość środka ciężkości pola i środka ciężkości brzegu
to, odpowiednio, odległość środka ciężkości pola i środka ciężkości brzegu 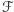 od osi.
od osi.
Guldin uzasadnił je, sprawdzając, że z objętością tak jest, gdy obracamy prostokąt o boku równoległym do osi obrotu, a z polem powierzchni - gdy obracamy odcinek.

Z obracania prostokąta otrzymamy walec o promieniu 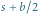 z wyciętym walcem o promieniu
z wyciętym walcem o promieniu 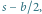
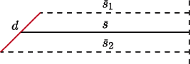
A potem stwierdził, że pole powierzchni można z dowolną dokładnością przybliżyć prostokącikami, a obwód odcineczkami i sprawdził, że środki ciężkości przy takim przybliżaniu zachowują się jak należy.
W niektórych książkach można znaleźć uogólnienie reguł Guldina, które przypisuje się żyjącemu 1300 lat wcześniej Pappusowi. W myśl tego uogólnienia można nie tylko mówić o obrotach, ale też o dowolnym ruchu. Wtedy we wzorach należy zastąpić 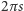 i
i 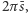 odpowiednio, przez drogę środka ciężkości powierzchni i drogę środka ciężkości brzegu
odpowiednio, przez drogę środka ciężkości powierzchni i drogę środka ciężkości brzegu 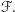
Faktycznie, np. dla przesunięcia w kierunku prostopadłym do płaszczyzny figury  tak jest. I jeszcze w bardzo wielu przypadkach. Ale twierdzenia matematyki muszą być spełnione we wszystkich dopuszczonych przez założenia sytuacjach. A tu tak nie jest.
tak jest. I jeszcze w bardzo wielu przypadkach. Ale twierdzenia matematyki muszą być spełnione we wszystkich dopuszczonych przez założenia sytuacjach. A tu tak nie jest.
Czytelnik Ambitny znajdzie przykłady przeczące tak śmiałemu uogólnieniu, a nawet wskaże, jak należałoby wzmocnić założenia, by uogólnienie uratować. Mniej ambitny znajdzie odpowiedź w numerze.
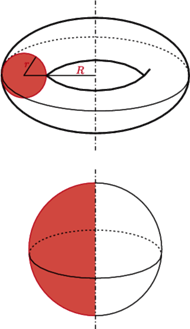
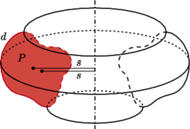
A my wrócimy do oryginalnych reguł Guldina, by obliczyć objętość i pole powierzchni torusa. Torus to bryła powstała w wyniku obracania koła wokół prostej leżącej w jego płaszczyźnie i niemającej z tym kołem punktów wspólnych. Środek ciężkości powierzchni koła jest też środkiem ciężkości ograniczającego je okręgu - to środek koła (gdyby było inaczej, obracając koło, otrzymalibyśmy wiele środków ciężkości). Zatem (patrz rysunek) 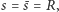 pole obracanego koła to
pole obracanego koła to 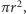 a długość ograniczającego je okręgu to
a długość ograniczającego je okręgu to 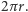 Mamy więc
Mamy więc

A na zakończenie zagadka: przyjrzyjmy się półkolu - czy bliżej odcinającej je średnicy leży środek ciężkości powierzchni półkola, czy też ograniczającego je półokręgu? Zapytajmy o to kolegów, a sami obliczmy.
Z obracania półkola względem odcinającej go średnicy otrzymujemy kulę - jej objętość to 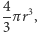 a pole powierzchni to
a pole powierzchni to 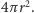 Z reguł Guldina mamy więc
Z reguł Guldina mamy więc

A więc środek ciężkości półkola leży bliżej średnicy niż środek półokręgu. Czy koledzy zgadli?
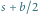 z wyciętym walcem o promieniu
z wyciętym walcem o promieniu 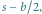 czyli bryłę o objętości
czyli bryłę o objętości