Co to jest?
Marian Smoluchowski
Ruchy Browna (II)
W poprzednim numerze Delty opisaliśmy zmagania fizyków XIX wieku z problemem tzw. ruchów Browna. Przypomnijmy podstawowe fakty. W roku 1827 Robert Brown odkrył zygzakowate ruchy wykonywane przez drobne ziarenka zawieszone w cieczy. Ruchy te obserwowano dla wszystkich substancji, o ile zostały one tak rozdrobnione, że ziarenka miały średnicę co najwyżej kilku mikronów. Próby wyjaśnienia przyczyn ruchów Browna napotkały poważne trudności...
Wszystkie hipotezy sprowadzające owe przyczyny do działania czynników zewnętrznych po konfrontacji z doświadczeniem musiały zostać odrzucone. Wyjaśnienie zagadki na gruncie teorii kinetyczno-molekularnej również wydawało się niezadowalające. Jeżeli bowiem przyjmiemy, że ruchy Browna są wynikiem zderzeń molekuł cieczy z zawieszonymi w niej ziarenkami, to: po pierwsze, proste oszacowanie wykazuje, że prędkość, jaką uzyska ziarenko na skutek jednego zderzenia z molekułą cieczy, ma niezwykle małą wartość; po drugie, jak sugerowali przeciwnicy hipotezy atomowej, ziarenka są bombardowane równomiernie ze wszystkich stron i w rezultacie nie powinny w ogóle się poruszać. Co więcej, jeżeli wyliczymy średnią prędkość ziarenek na podstawie zasady ekwipartycji energii, to uzyskamy wartość ok. 10 tys. razy większą niż obserwowana w eksperymentach. Tak wyglądała sytuacja na przełomie XIX i XX wieku. Wiek XX przyniósł jednak rozwiązanie zagadki. A oto, jak do tego doszło.
Pierwszym ważnym momentem było skonstruowanie przez Siedentopfa i Zsigmondy'ego w roku 1903 tzw. ultramikroskopu.
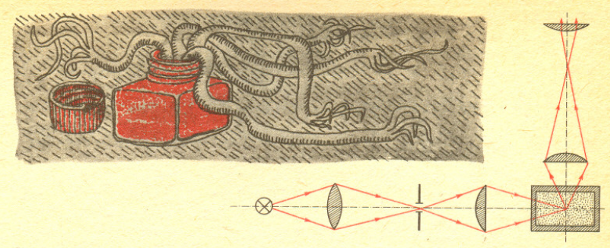
Schemat ultramikroskopu.
Zasada działania tego przyrządu była bardzo prosta. Od 1868 roku znano zjawisko Tyndalla polegające na rozpraszaniu światła przez ośrodki mętne - ośrodki, które są właśnie omawianymi przez nas zawiesinami drobnych cząsteczek w cieczach i gazach. Wiązka światła prostopadłym do wiązki. Do obserwatora dociera wtedy tylko światło rozproszone. Na ciemnym tle widoczne są jasne punkciki wszędzie tam, gdzie znajdują się ziarenka zawiesiny. W ten sposób można obserwować ziarenka o rozmiarach nawet rzędu kilku nanometrów 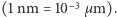 Niektórych Czytelników może ten fakt zaskoczyć. Przecież wiadomo, że zdolność rozdzielcza mikroskopu jest co do rzędu wielkości równa długości fali świetlnej, a ta zawiera się w granicach ok.
Niektórych Czytelników może ten fakt zaskoczyć. Przecież wiadomo, że zdolność rozdzielcza mikroskopu jest co do rzędu wielkości równa długości fali świetlnej, a ta zawiera się w granicach ok. 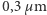 do
do 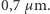 Nie ma w tym żadnej sprzeczności. Ultramikroskop nie pozwala bowiem dostrzec kształtów ziarenek, lecz jedynie stwierdzić ich obecność w danym punkcie przestrzeni. Jest to jednak całkowicie wystarczające, by śledzić ich ruchy. Przypomnijmy, że intensywność ruchów Browna wzrastała wraz ze zmniejszeniem się rozmiarów cząsteczek zawiesiny. Tymczasem ultramikroskop pozwolił na obserwację ziarenek o średnicy ok. 100 razy mniejszej od średnicy tych, które widziano przez zwykły mikroskop.
Nie ma w tym żadnej sprzeczności. Ultramikroskop nie pozwala bowiem dostrzec kształtów ziarenek, lecz jedynie stwierdzić ich obecność w danym punkcie przestrzeni. Jest to jednak całkowicie wystarczające, by śledzić ich ruchy. Przypomnijmy, że intensywność ruchów Browna wzrastała wraz ze zmniejszeniem się rozmiarów cząsteczek zawiesiny. Tymczasem ultramikroskop pozwolił na obserwację ziarenek o średnicy ok. 100 razy mniejszej od średnicy tych, które widziano przez zwykły mikroskop.
Eksperymentatorzy drugiej połowy XIX w. mieli poważne trudności z uzyskaniem ilościowych wyników dla ruchów Browna i posługiwali się w związku z tym głównie subiektywnym pojęciem ich intensywności. Teraz dysponowali przyrządem, który umożliwił im precyzyjne pomiary. Brakowało tylko teorii. Pełną teorię ruchów Browna sformułowano niebawem. W 1905 r. A. Einstein opublikował bowiem pracę, w której podał prawidłowy opis tych ruchów traktując je jako szczególny przypadek procesu dyfuzji i otrzymując w rezultacie wzór na przesunięcie cząsteczek zawiesiny. Einstein posługiwał się jednak abstrakcyjnym jak na owe czasy sformułowaniem fizyki statystycznej i nie wnikał w mechanizm zjawiska. Mechanizm ten pozostawał w związku z tym dalej niejasny. Ale w rok później pod wpływem pracy Einsteina wyniki swoich przemyśleń przedstawił M. Smoluchowski. Używając prostych argumentów ostatecznie rozwikłał zagadkę. Prześledźmy szczegóły jego rozumowania.
Swoje rozważania rozpoczął Smoluchowski od odparcia zarzutów Nägeliego. Stwierdził, że rzeczywiście przyrost prędkości ziarenka na skutek zderzenia z jedną molekułą cieczy jest bardzo mały, ale wyciąganie z tego wniosku, iż ziarenko będzie stało w miejscu to błąd. Jak sam pisze: "Jest to taki sam błąd rozumowania, jak gdyby człowiek uprawiający grę hazardową (np. rzucanie kostki) sądził, że nigdy większej straty ani też większego zysku mieć nie będzie, niż wynosi stawka na jeden rzut. Wiemy dobrze, że szczęście i nieszczęście zwykle niezupełnie się równoważą; że im dłużej gra trwa, tym większa jest przeciętna suma albo wygrana, albo stracona". Aby uściślić ten argument, Smoluchowski przytoczył proste obliczenie. Niech prawdopodobieństwa rzutów korzystnego i niekorzystnego są równe 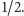 Prawdopodobieństwo
Prawdopodobieństwo 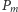 otrzymania w
otrzymania w  próbach
próbach 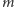 wyników korzystnych i
wyników korzystnych i 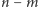 niekorzystnych, a zatem nadwyżki
niekorzystnych, a zatem nadwyżki 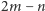 jednych nad drugimi, dane jest przez rozkład Bernoulli'ego
jednych nad drugimi, dane jest przez rozkład Bernoulli'ego

Stąd znajdujemy, że średnia 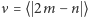 wartości bezwzględnej tej nadwyżki wynosi (dla parzystych
wartości bezwzględnej tej nadwyżki wynosi (dla parzystych  )
)

Dla bardzo dużych 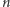 stosując wzór Stirlinga można sprowadzić powyższą średnią do
stosując wzór Stirlinga można sprowadzić powyższą średnią do

czyli 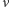 jest proporcjonalne do pierwiastka kwadratowego z liczby prób. Ziarenko zawiesiny uderzane jest przez molekuły cieczy średnio
jest proporcjonalne do pierwiastka kwadratowego z liczby prób. Ziarenko zawiesiny uderzane jest przez molekuły cieczy średnio 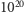 razy w ciągu sekundy. Zatem przeciętna nadwyżka uderzeń z jednej strony nad uderzeniami z drugiej strony będzie w tym czasie
razy w ciągu sekundy. Zatem przeciętna nadwyżka uderzeń z jednej strony nad uderzeniami z drugiej strony będzie w tym czasie 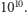 Jeśli nawet wynik pojedynczego zderzenia jest bardzo mały, to sumaryczny efekt może być znaczny. Ziarenko będzie się poruszać!
Jeśli nawet wynik pojedynczego zderzenia jest bardzo mały, to sumaryczny efekt może być znaczny. Ziarenko będzie się poruszać!

Pozostała do wyjaśnienia sprawa średniej prędkości. Aby rozwikłać ten problem, Smoluchowski postawił na początek pytanie: jaki jest tor ruchu cząsteczki Browna? Zauważmy, stwierdził, że cząsteczka ta ma ogromną masę w porównaniu z masą pojedynczej molekuły cieczy. Również średnia wartość jej prędkości jest zgodnie z zasadą ekwipartycji energii bardzo duża. W związku z tym jedno czy kilka uderzeń ze strony molekuł cieczy nie jest w stanie zmienić kierunku ruchu rozpędzonej cząsteczki Browna. Będzie się ona poruszać po linii prostej przez bardzo długi okres czasu w porównaniu ze średnim czasem między kolejnymi zderzeniami, który jest rzędu 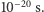 Będzie się tak poruszać praktycznie aż do momentu zatrzymania. Po czym, na skutek fluktuacji liczby zderzeń z różnych stron zostanie rozpędzona w innym kierunku itd. Zatem tor jej ruchu będzie się składał z prostych odcinków ukierunkowanych w sposób chaotyczny. Jeżeli chcielibyśmy zmierzyć prędkość ziarenka i porównać ją z wartością wynikającą z zasady ekwipartycji energii, to musielibyśmy zrobić to na jednym z tych odcinków. Tymczasem, jak oszacował Smoluchowski, średni czas ruchu cząsteczki Browna po prostej jest rzędu
Będzie się tak poruszać praktycznie aż do momentu zatrzymania. Po czym, na skutek fluktuacji liczby zderzeń z różnych stron zostanie rozpędzona w innym kierunku itd. Zatem tor jej ruchu będzie się składał z prostych odcinków ukierunkowanych w sposób chaotyczny. Jeżeli chcielibyśmy zmierzyć prędkość ziarenka i porównać ją z wartością wynikającą z zasady ekwipartycji energii, to musielibyśmy zrobić to na jednym z tych odcinków. Tymczasem, jak oszacował Smoluchowski, średni czas ruchu cząsteczki Browna po prostej jest rzędu 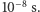 Ruchu o tak krótkim czasie trwania nie jesteśmy w stanie obserwować nawet pod ultramikroskopem. Stąd Smoluchowski wyciągnął natychmiast wniosek, że nie pomiar średniej prędkości, ale pomiar średniego oddalenia się ziarenka od położenia początkowego może być ilościowym testem przewidywań teorii kinetyczno-molekularnej. W celu wyznaczenia tego oddalenia Smoluchowski przyrównał ruch cząsteczki Browna do procesu, który dziś zwiemy błądzeniem przypadkowym. W rezultacie otrzymał następujący wzór, poprzednio wyprowadzony przez Einsteina,
Ruchu o tak krótkim czasie trwania nie jesteśmy w stanie obserwować nawet pod ultramikroskopem. Stąd Smoluchowski wyciągnął natychmiast wniosek, że nie pomiar średniej prędkości, ale pomiar średniego oddalenia się ziarenka od położenia początkowego może być ilościowym testem przewidywań teorii kinetyczno-molekularnej. W celu wyznaczenia tego oddalenia Smoluchowski przyrównał ruch cząsteczki Browna do procesu, który dziś zwiemy błądzeniem przypadkowym. W rezultacie otrzymał następujący wzór, poprzednio wyprowadzony przez Einsteina,

gdzie 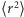 - średni kwadrat przesunięcia ziarenka w płaszczyźnie obserwacji w czasie
- średni kwadrat przesunięcia ziarenka w płaszczyźnie obserwacji w czasie 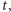
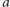 - promień ziarenka,
- promień ziarenka, 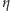 -współczynnik lepkości cieczy,
-współczynnik lepkości cieczy, 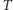 - temperatura,
- temperatura, 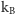 stała Boltzmanna równa
stała Boltzmanna równa 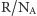 (
( 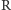 stała gazowa,
stała gazowa, 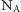 liczba Avogadro).
liczba Avogadro).
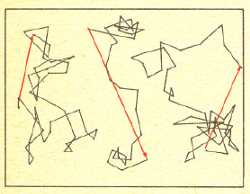
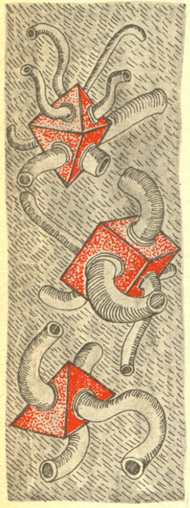
Położenia cząsteczek Browna o średnicy ok. 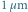 rejestrowane co 30 sekund. Kolejność zaznaczono łącząc punkty odcinkami. Odcinek czerwony to całkowite przesuniecie cząsteczki Browna .
rejestrowane co 30 sekund. Kolejność zaznaczono łącząc punkty odcinkami. Odcinek czerwony to całkowite przesuniecie cząsteczki Browna .
Już wstępna analiza tego wzoru przekonuje nas, że Einstein i Smoluchowski znaleźli właściwe rozwiązanie. Przeciętne przesunięcie cząsteczki Browna, które można utożsamiać z intensywnością jej ruchów, jest bowiem proporcjonalne do temperatury, odwrotnie proporcjonalne do lepkości cieczy i rozmiarów cząsteczki oraz nie zależy od substancji, z której cząsteczka jest zbudowana. Dokładnie tak, jak wynikało to z ówcześnie dostępnych jakościowych wyników obserwacji. Nie musiano ograniczać się jednak tylko do stwierdzenia tego rodzaju zgodności. Dysponując ultramikroskopem eksperymentatorzy mogli natychmiast przystąpić do precyzyjnych pomiarów.
Pierwsze rezultaty ilościowe, jakie otrzymał Swedberg w 1907 roku, potwierdzały przewidywaną przez wzór Einsteina-Smoluchowskiego zależność od lepkości ośrodka i promienia cząsteczek. Decydujące znaczenie miały jednak wyniki prac Perrina z roku 1908. Perrin udoskonalił znacznie metody pomiarów opracowując m.in. metodę sporządzania zawiesin składających się z ziarenek o jednakowych rozmiarach. Przyjmując, że wzór na średni kwadrat przesunięcia cząsteczki Browna jest prawidłowy, wyznaczył za jego pomocą na podstawie danych eksperymentalnych liczbę Avogadro. Uzyskany przez niego wynik: 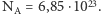 Znane ówcześnie wartości liczby Avogadro otrzymywane na zupełnie innej drodze, m.in. przez samego Perrina, wahały się w granicach od
Znane ówcześnie wartości liczby Avogadro otrzymywane na zupełnie innej drodze, m.in. przez samego Perrina, wahały się w granicach od 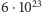 do
do 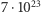 (obecnie znamy tę liczbę z dużą dokładnością, jest ona równa
(obecnie znamy tę liczbę z dużą dokładnością, jest ona równa 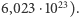 Taka zgodność rezultatów musiała przekonać najzagorzalszych przeciwników hipotezy atomowej. Tak też się stało. Jeden z głównych oponentów W. Ostwald napisał w 1909 r.:
Taka zgodność rezultatów musiała przekonać najzagorzalszych przeciwników hipotezy atomowej. Tak też się stało. Jeden z głównych oponentów W. Ostwald napisał w 1909 r.:
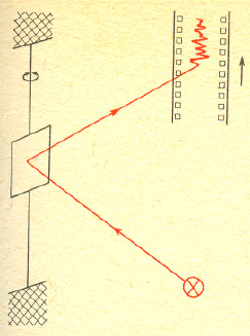
Schemat eksperymentu Kapplera ze zwierciadełkiem Smoluchowskiego.
Doszedłem do przekonania, że od niedawna posiadamy doświadczalny dowód dyskretnej czy ziarnistej natury materii, którego od setek, a nawet tysięcy lat daremnie szukała hipoteza atomistyczna.
Rozważania Smoluchowskiego znalazły jeszcze jedno potwierdzenie w pięknych doświadczeniach wykonanych w latach trzydziestych XX w. przez E. Kapplera. Otóż Kappler przeprowadził szereg eksperymentów ze zwierciadełkiem zawieszonym na sprężystej nici. Zwierciadełko takie bombardowane przez cząsteczki powietrza wykonuje niewielkie, chaotyczne drgania, które są niczym innym jak odpowiednikiem ruchów Browna. Możemy je obserwować w prosty sposób kierując na zwierciadełko promień świetlny i rejestrując na ekranie ślad promienia odbitego. Teorię tego zjawiska opracował już wcześniej Smoluchowski. W porównaniu z teorią "klasycznych" ruchów Browna wymagała ona uwzględnienia siły sprężystości nici. W oparciu o rezultaty Smoluchowskiego i wyniki pomiarów Kappler wyznaczył liczbę Avogadro z dokładnością do 1%. Ale nie tylko. W miejsce ekranu wstawił bowiem kliszę fotograficzną.
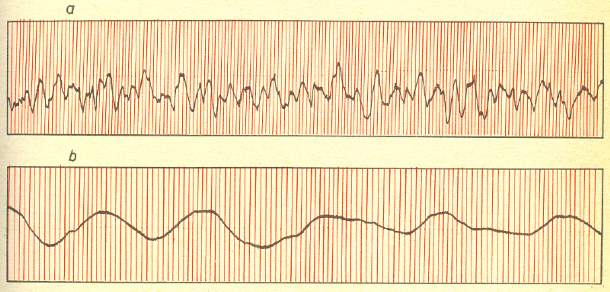
Typowe wyniki eksperymentu Kapplera. Prędkość przesuwania kliszy:
a) 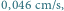 b)
b) 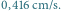 Odstęp miedzy sąsiednimi liniami poziomymi: a)
Odstęp miedzy sąsiednimi liniami poziomymi: a) 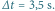 b)
b) 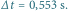
Przesuwając kliszę uzyskiwał na niej obraz drgań zwierciadełka w postaci zygzakowatej krzywej. Im większa była szybkość przesuwania kliszy, tym więcej szczegółów w postaci coraz mniejszych zygzaków było rejestrowanych. Ale po osiągnięciu pewnej szybkości dalsze jej zwiększanie nie powodowało już wykrywania nowych zwrotów zwierciadełka. To, co Smoluchowskiemu wydawało się niemożliwe, stało się faktem. Kappler rejestrował elementarne ruchy zwierciadełka - odpowiadające prostoliniowym ruchom cząsteczki Browna! Mógł zatem wyznaczyć ich średnią prędkość. Wynik zgadzał się doskonale z zasadą ekwipartycji energii.
Warto wskazać czynniki, które umożliwiły ten pomiar. Po pierwsze, ośrodkiem był bardzo rozrzedzony gaz (ciśnienie 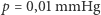 ), co spowodowało w stosunku do cieczy drastyczne zmniejszenie częstości zderzeń molekuł ośrodka z jednostką powierzchni umieszczonego w nim ciała. Poza tym intensywność ruchów Browna zwierciadełka zależała jedynie od momentu skręcającego nici. Zwierciadełko mogło być zatem bardzo duże (jedyne ograniczenie to wytrzymałość nici) i w konsekwencji mogło mieć duży moment bezwładności. W przypadku ziarenka zawieszonego w cieczy tor zakreślany w ciągu 1 sekundy składał się z około
), co spowodowało w stosunku do cieczy drastyczne zmniejszenie częstości zderzeń molekuł ośrodka z jednostką powierzchni umieszczonego w nim ciała. Poza tym intensywność ruchów Browna zwierciadełka zależała jedynie od momentu skręcającego nici. Zwierciadełko mogło być zatem bardzo duże (jedyne ograniczenie to wytrzymałość nici) i w konsekwencji mogło mieć duży moment bezwładności. W przypadku ziarenka zawieszonego w cieczy tor zakreślany w ciągu 1 sekundy składał się z około 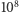 prostych odcinków. W doświadczeniu Kapplera opisane czynniki spowodowały, że tych odcinków było bardzo mało, średnio jeden na kilka sekund. Można je było zatem obserwować.
prostych odcinków. W doświadczeniu Kapplera opisane czynniki spowodowały, że tych odcinków było bardzo mało, średnio jeden na kilka sekund. Można je było zatem obserwować.

Pierwsze dojrzałe teorie kosmologiczne (mówiące o powstaniu i rozwoju Wszechświata) pojawiły się w latach dwudziestych naszego stulecia. Za swą podstawę miały ogólną teorię względności, a dokładniej modele Friedmana z tej teorii wyprowadzone. Ogromna popularność tematu i wielka ilość odkryć astronomicznych sprawiły, że podstawa taka przestała wystarczać. Zaczęto coraz jawniej postulować, aby kosmologię oprzeć na całej fizyce i by za stan, od którego odtwarzamy wstecz minione dzieje Wszechświata aż do jego początku, uznać całość naszej wiedzy o Wszechświecie, a więc nie tylko istnienie galaktyk czy gwiazd, lecz także by nie zapominać o tym, że na Ziemi pojawiło się życie. Słowem, zażądano od kosmologii, aby jej modele były na tyle precyzyjne, by przewidywały również zaistnienie kosmologów. Niżej przedstawiamy artykuł o tym, jak ten postulat jest omawiany wśród astronomów.
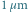 rejestrowane co 30 sekund. Kolejność zaznaczono łącząc punkty odcinkami. Odcinek czerwony to całkowite przesuniecie cząsteczki Browna .
rejestrowane co 30 sekund. Kolejność zaznaczono łącząc punkty odcinkami. Odcinek czerwony to całkowite przesuniecie cząsteczki Browna .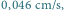 b)
b) 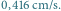 Odstęp miedzy sąsiednimi liniami poziomymi: a)
Odstęp miedzy sąsiednimi liniami poziomymi: a) 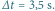 b)
b) 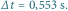
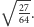 W późniejszych pracach Smoluchowskiego rozbieżność ta już nie wystepowała.
W późniejszych pracach Smoluchowskiego rozbieżność ta już nie wystepowała.