Jak to działa?
Dlaczego woda wylewa się z wiadra?
Gdybyśmy wzięli wiadro pełne wody i udałoby nam się obrócić je tak, by swobodna powierzchnia wody była dnem, woda niemal natychmiast wylałaby się. Powszechnie znane jest doświadczenie z kartką, którą nakrywamy powierzchnię szklanki wypełnionej wodą, a następnie odwracamy naczynie i obserwujemy, że woda nie wylewa się.
Przyczyną jest obecność ciśnienia atmosferycznego, które jest większe niż ciśnienie hydrostatyczne tuż nad kartką. Siła parcia wynikająca z różnicy ciśnień jest skierowana ku górze i powstrzymuje ciecz przed wylaniem się. Jeśli jednak spróbujemy usunąć kartkę, natychmiast zmoczymy siebie i okolicę. Co dawała nam więc obecność kartki? W czym kartka lepsza jest niż powierzchnia cieczy? Z drugiej strony, jeśli weźmiemy wiadro w rozmiarze mini, np. flakonik po perfumach, i wypełnimy wodą, po obróceniu naczynia do góry dnem ciecz pozostanie w środku i nie wyleje się. Zatem rozmiar powierzchni ma tu znaczenie. Jaki tajemniczy mechanizm stoi za wylewaniem się wody z wiadra? Wydaje się, że jesteśmy tak przyzwyczajeni do tego zjawiska, że nie zadajemy sobie tego pytania, a tymczasem jest to bardzo ciekawe pole do popisu dla prostych modeli energetycznych.
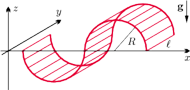
Rys. 1 Półwalcowe zaburzenie w uproszczonym modelu.
Poniżej przedstawimy rozumowanie zaczerpnięte z rosyjskiej książki S.S. Chilkiewicza. Jest to bardzo prosty model, który jednak pozwala uchwycić mechanizm fizyczny tego zjawiska i wyeksponować rolę sił napięcia powierzchniowego i grawitacji przy analizie niestabilności powierzchni.
Rozważamy zaburzenia powierzchni w formie fal o kształcie półwalców
(Rys. 1). Z powodu istnienia napięcia powierzchniowego
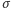 praca
związana ze zwiększeniem pola powierzchni rozdziału płynów wynosi
praca
związana ze zwiększeniem pola powierzchni rozdziału płynów wynosi
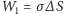 . Wygięciu powierzchni towarzyszy również przemieszczenie
pewnej masy wody, której energia potencjalna zmienia się. Jeśli rozważymy
pewną masę wody o środku masy na wysokości
. Wygięciu powierzchni towarzyszy również przemieszczenie
pewnej masy wody, której energia potencjalna zmienia się. Jeśli rozważymy
pewną masę wody o środku masy na wysokości
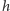 nad ziemią, jej
energia potencjalna wyniesie
nad ziemią, jej
energia potencjalna wyniesie
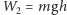 . W przypadku pojedynczego
,,zafalowania”, polegającego na wygięciu prostokątnego fragmentu powierzchni
o wymiarach
. W przypadku pojedynczego
,,zafalowania”, polegającego na wygięciu prostokątnego fragmentu powierzchni
o wymiarach
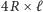 w dwa półwalce, z których jeden jest wypełniony
cieczą, zmiana pola powierzchni tego obszaru wyniesie
w dwa półwalce, z których jeden jest wypełniony
cieczą, zmiana pola powierzchni tego obszaru wyniesie

Wobec tego została wykonana praca

Z drugiej strony, zmieniła się również energia potencjalna wody. Jeżeli
środek masy porcji wody obniżył się o
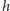 , to zmiana jego energii
potencjalnej wyniosła
, to zmiana jego energii
potencjalnej wyniosła
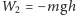 . Łatwo znajdujemy wysokość
środka masy układu, ponieważ nasze wybrzuszenia są półwalcami
o promieniu
. Łatwo znajdujemy wysokość
środka masy układu, ponieważ nasze wybrzuszenia są półwalcami
o promieniu
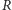 i długości
i długości
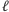 . Jeśli początkowo środek masy
wody, tworzącej półwalec, znajdował się na wysokości
. Jeśli początkowo środek masy
wody, tworzącej półwalec, znajdował się na wysokości
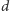 nad poziomem
powierzchni rozdziału faz, to teraz obniżył się o
nad poziomem
powierzchni rozdziału faz, to teraz obniżył się o
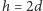 (po prostu
,,wykroiliśmy” półwalec wody znad powierzchni i ,,przykleiliśmy”
go do dna). Dla takiego półwalca położenie środka masy można
zapisać jako
(po prostu
,,wykroiliśmy” półwalec wody znad powierzchni i ,,przykleiliśmy”
go do dna). Dla takiego półwalca położenie środka masy można
zapisać jako

Całkowita zmiana energii przy tworzeniu się takiego zaburzenia wynosi więc

Otrzymaliśmy wyrażenie wielomianowe względem
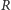 . Zbadajmy je.
. Zbadajmy je.
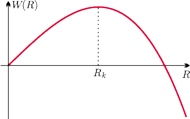
Rys. 2 Schematyczny wykres zależności energii zaburzenia od „długości” fali.
Zadanie, które stoi teraz przed nami, jest bardzo podobne do następującego
zagadnienia: rozważmy ciało poruszające się na prostej, którego energia
potencjalna zależy od położenia
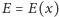 . Zmiana energii potencjalnej
ciała jest równa pracy wykonanej nad ciałem, czyli pracy sił pola wziętej ze
znakiem minus:
. Zmiana energii potencjalnej
ciała jest równa pracy wykonanej nad ciałem, czyli pracy sił pola wziętej ze
znakiem minus:
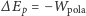 . Jeśli wybierzemy dostatecznie małą
odległość
. Jeśli wybierzemy dostatecznie małą
odległość
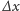 , to pracę sił pola możemy zapisać jako
, to pracę sił pola możemy zapisać jako
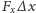 .
Możemy zatem zapisać wyrażenie na lokalną wartość siły w zależności
od położenia jako
.
Możemy zatem zapisać wyrażenie na lokalną wartość siły w zależności
od położenia jako

W przypadku, gdy przemieszczamy ciało ku ,,górce” energii potencjalnej, siła będzie skierowana przeciwnie do kierunku wzrostu energii potencjalnej (co jest intuicyjne). Położenie na szczycie będzie położeniem równowagi nietrwałej, bo na wychylone z niego ciało działać będzie siła, która zwiększy wychylenie – za chwilę wykorzystamy ten wniosek. Płynie stąd jeszcze jeden morał – położenie o minimalnej energii będzie położeniem równowagi trwałej.
Przedstawiony na rysunku 2 przebieg funkcji
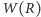 wskazuje
istnienie maksimum. Okazuje się więc, że istnieje krytyczna wartość
promienia
wskazuje
istnienie maksimum. Okazuje się więc, że istnieje krytyczna wartość
promienia
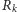 , powyżej której amplituda fali będzie nieograniczenie
wzrastać, bo dla
, powyżej której amplituda fali będzie nieograniczenie
wzrastać, bo dla
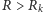 zwiększenie amplitudy będzie prowadziło
do zmniejszenia energii zaburzenia. Zysk energetyczny wynikający
z obniżenia położenia środka masy będzie większy aniżeli strata
związana z powiększaniem pola powierzchni granicy faz. Dzieje się tak
dlatego, że jesteśmy tu świadkami konkurencji sił powierzchniowych
(rosnących z pewną charakterystyczną dla układu skalą długości
zwiększenie amplitudy będzie prowadziło
do zmniejszenia energii zaburzenia. Zysk energetyczny wynikający
z obniżenia położenia środka masy będzie większy aniżeli strata
związana z powiększaniem pola powierzchni granicy faz. Dzieje się tak
dlatego, że jesteśmy tu świadkami konkurencji sił powierzchniowych
(rosnących z pewną charakterystyczną dla układu skalą długości
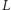 jak
jak
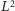 ) i sił objętościowych (rosnących jak
) i sił objętościowych (rosnących jak
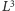 ). Dla dostatecznie
dużych długości wkład do całkowitej energii cieczy pochodzący od
energii objętościowej (potencjalnej) przeważa. Można teraz znaleźć
maksimum funkcji
). Dla dostatecznie
dużych długości wkład do całkowitej energii cieczy pochodzący od
energii objętościowej (potencjalnej) przeważa. Można teraz znaleźć
maksimum funkcji
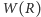 i przekonać się, że interesująca nas
wartość promienia to
i przekonać się, że interesująca nas
wartość promienia to

Dla
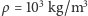 ,
,
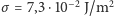 otrzymujemy krytyczny
promień
otrzymujemy krytyczny
promień
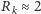 mm. Stąd długość fali
mm. Stąd długość fali
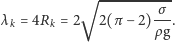
W przypadku fal ,,walcowych” znaleźliśmy zależność zmiany energii
zaburzenia od promienia zaburzającej fali. Jasne jest teraz, że narastać
będą takie zaburzenia, dla których
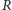 jest odpowiednio duże.
Zaburzenia, których
jest odpowiednio duże.
Zaburzenia, których
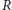 znajdzie się na lewo od maksimum, będą
miały tendencję do zanikania, natomiast te na prawo będą powodowały
niestabilność powierzchni.
znajdzie się na lewo od maksimum, będą
miały tendencję do zanikania, natomiast te na prawo będą powodowały
niestabilność powierzchni.
Bardzo podobne rozumowanie prowadzi się w klasycznej teorii przy analizie
tworzenia się w układzie metastabilnym zarodków nowej fazy. Przypuśćmy
mianowicie, że pojemnik z gazem ochłodzimy poniżej temperatury
wrzenia. Mamy wówczas do czynienia właśnie ze stanem metastabilnym –
z termodynamicznego punktu widzenia dla układu korzystniejsze jest
przebywanie w stanie ciekłym, jednakże przejście fazowe wymaga
powstania zaczątków fazy ciekłej, czyli małych kropelek. Utworzenie
kropelki jest związane z pewnym kosztem energetycznym, który wynika
z istnienia napięcia powierzchniowego. Mamy więc również do czynienia
z gęstością energii powierzchniowej oraz gęstością energii objętościowej
i konkurencją tych dwóch wkładów do całkowitej energii układu
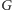 .
Prowadzi to do wniosku, że i w tym przypadku również istnieje bariera
przy tworzeniu się jądra kondensacji, a zależność zmiany energii
(ściślej mówiąc – energii swobodnej Gibbsa) od promienia kropli
ma także charakter wielomianu trzeciego stopnia. W związku z tym
powstające w układzie w sposób przypadkowy zarodki, jeśli są za małe,
szybko znikają, parując ponownie, bo dla
.
Prowadzi to do wniosku, że i w tym przypadku również istnieje bariera
przy tworzeniu się jądra kondensacji, a zależność zmiany energii
(ściślej mówiąc – energii swobodnej Gibbsa) od promienia kropli
ma także charakter wielomianu trzeciego stopnia. W związku z tym
powstające w układzie w sposób przypadkowy zarodki, jeśli są za małe,
szybko znikają, parując ponownie, bo dla
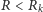 zmniejszenie
promienia zmniejsza energię układu. Z kolei powstanie odpowiednio dużej
kropli jest dalece mniej prawdopodobne. W praktyce okazuje się, że
zarodek krytyczny zawiera około 200 atomów (cząsteczek) i ma rozmiary
rzędu 6–10 Å.
zmniejszenie
promienia zmniejsza energię układu. Z kolei powstanie odpowiednio dużej
kropli jest dalece mniej prawdopodobne. W praktyce okazuje się, że
zarodek krytyczny zawiera około 200 atomów (cząsteczek) i ma rozmiary
rzędu 6–10 Å.
Ale dla przypadku fal na odwróconej powierzchni to, oczywiście, zbyt prosty model. Przede wszystkim nie pozwala nam on rozróżnić dwóch bardzo ważnych parametrów – długości fali i amplitudy. W przypadku fal sinusoidalnych analiza jest o wiele bardziej skomplikowana. Zjawisko niestabilności powierzchni rozdzielającej dwa płyny w polu grawitacyjnym, gdy gęstość górnego płynu jest większa niż dolnego, nazywa się niestabilnością Rayleigha–Taylora. Czytelnika zainteresowanego dokładniejszą analizą niestabilności fal sinusoidalnych na powierzchni rozdziału płynów odsyłamy do podręczników mechaniki płynów (zwięzły opis można znaleźć np. w książce Fabera). Przedstawione tam kryterium, otrzymane w bardziej wyrafinowany sposób, różni się od powyższego jedynie współczynnikiem liczbowym

Jeśli porównamy to z długością fali wyliczoną w ramach przedstawionego powyżej modelu, okaże się, że wartości te różnią się dość znacznie

jednak zaskakująco prosty model fal o przekroju półkolistym daje dobry rząd wielkości przewidywanej długości fali.
Tym samym rozwiązała się nasza zagadka – woda wylewa się z wiadra, bo jest ono duże. /Srednica otworu jest na tyle duża, że na powierzchni cieczy mają szansę wytworzyć się dostatecznie długie, niestabilne fale. Oczywiście, kartka, którą przykryjemy powierzchnię, bardzo efektywnie tłumi takie zaburzenia. W przypadku flakonika perfum lub aromatu do ciasta średnica otworu jest na tyle mała (rzędu kilku milimetrów), że nie mogą tam powstać dłuższe fale, zaburzenia zaś o mniejszej długości fali są tłumione i nie prowadzą do niestabilności powierzchni, więc i bez kartki widzimy efekty działania ciśnienia atmosferycznego. Przekonać można się o tym w jeszcze jeden sposób – zamiast kartką, można nakryć szklankę płaskim sitkiem i kartką, odwrócić i delikatnie usunąć kartkę – woda utrzyma się, bo sitko wytłumia długie, ,,niebezpieczne” fale.
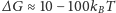 , więc
prawdopodobieństwo pojawienia się takiego zarodka, które można
oszacować jako
, więc
prawdopodobieństwo pojawienia się takiego zarodka, które można
oszacować jako
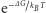 , jest maleńkie.
, jest maleńkie.