Galileusz Arystotelesa ośmieszył... A co na to Newton?

W Małej Delcie z czerwca 2018 M. K. opisał prosty dowód podany przez Galileusza, pokazujący, że swobodne spadanie ciał nie może być ruchem, w kórym, jak twierdził Stagiryta, prędkość spadającego ciała jest proporcjonalna do przebytej przez nie drogi. Galileusz posłużył się prostymi argumentami (wszak mechanika analityczna jeszcze nie istniała) logiczno-geometrycznymi. Nie będę ich tu cytował, kto nie pamięta, łatwo je w Delcie odnajdzie.

Popatrzmy jednak na taki ruch newtonowskimi oczyma. Równanie 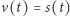$|v(t) = s(t)$ możemy zapisać w postaci równania różniczkowego

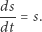ds-= s. dt

Całkując je, otrzymujemy

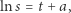ln s = t+ a,

gdzie 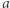$a$ jest stałą całkowania. Jeśli teraz wybierzemy (za Galileuszem) na drodze poruszającego się ciała punkty

−n sn = 2 ,

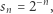to po podstawieniu do ostatniego równania otrzymamy czas 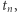$tn,$ w kórym poruszające się ciało znajdzie się w punkcie $|sn$ :

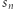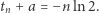tn + a = −n ln2.

Widzimy zatem, że

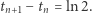tn+1− tn = ln2.

(Istotnie, jest to więcej niż 1/2). Każdy z nieskończonej liczby odcinków jest w tym ruchu przebywany w takim samym czasie o wartości 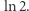$ln 2.$

Jeśli rozwiązanie równania ruchu zapiszemy w postaci explicite

t s = be ,

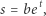gdzie 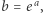$b = ea,$ to widzimy, że punkt 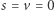$s = v = 0$ odpowiada wartości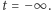 $|t = −∞ .$

Tak więc ciało poruszające się ruchem, o którym mówił Arystoteles, nigdy nie może być w spoczynku 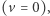$(v = 0),$ chyba że myślimy o epoce, zanim Matka Ziemia wyłoniła się z Chaosu i we śnie urodziła Uranosa...