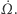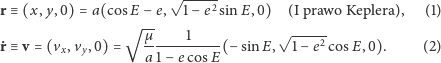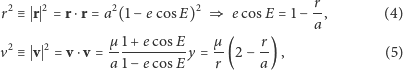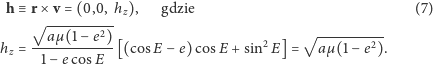O obrotach... wektorów i satelitów
Pierwszy polski satelita naukowy BRITE-Lem wystartował 21 listopada 2013 roku o godzinie 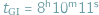 czasu polskiego (CSE = UTC + 1h) z bazy Jasny w Rosji a na orbicie znalazł się 956 s później, w chwili, którą oznaczymy
czasu polskiego (CSE = UTC + 1h) z bazy Jasny w Rosji a na orbicie znalazł się 956 s później, w chwili, którą oznaczymy 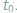 Operator rakiety "Dniepr", rosyjsko-ukraińsko-kazachska korporacja Kosmotras, podała przewidywane współrzędne satelity w chwili
Operator rakiety "Dniepr", rosyjsko-ukraińsko-kazachska korporacja Kosmotras, podała przewidywane współrzędne satelity w chwili 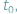 w nierotującym względem gwiazd układzie kartezjańskim ze środkiem w centrum Ziemi.
w nierotującym względem gwiazd układzie kartezjańskim ze środkiem w centrum Ziemi.

Oś  tego układu współrzędnych jest skierowana ku biegunowi północnemu, natomiast osie
tego układu współrzędnych jest skierowana ku biegunowi północnemu, natomiast osie  i
i 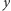 są skierowane w ten sposób, że w chwili startu
są skierowane w ten sposób, że w chwili startu 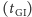 Greenwich leżało w płaszczyźnie
Greenwich leżało w płaszczyźnie 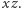 W takim układzie współrzędnych pracują urządzenia nawigacyjne rakiety, włączane w chwili startu
W takim układzie współrzędnych pracują urządzenia nawigacyjne rakiety, włączane w chwili startu 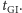 Współrzędne satelity w chwili wejścia na orbitę
Współrzędne satelity w chwili wejścia na orbitę 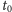 w tym układzie to
w tym układzie to 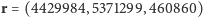 m i prędkość
m i prędkość 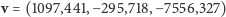 m/s. Spróbujemy odpowiedzieć na pytanie, czy i w jakim kierunku satelita mógł być widziany o godzinie
m/s. Spróbujemy odpowiedzieć na pytanie, czy i w jakim kierunku satelita mógł być widziany o godzinie 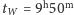 CSE tego dnia ze zlokalizowanego w Warszawie punktu o współrzędnych kartezjańskich
CSE tego dnia ze zlokalizowanego w Warszawie punktu o współrzędnych kartezjańskich 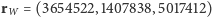 w układzie rotującym z Ziemią, w którym Greenwich zawsze leży w płaszczyźnie
w układzie rotującym z Ziemią, w którym Greenwich zawsze leży w płaszczyźnie 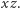
Od razu zastrzegę, że by uprościć wywody, zaniedbamy wpływ spłaszczenia Ziemi i oporu resztek atmosfery na ruch satelity i skorzystamy z równań opisujących ruch satelity po elipsie keplerowskiej wokół obiektu o sferycznie symetrycznym rozkładzie masy (który może być równoważnie zastąpiony masą punktową). Główna konsekwencja zaniedbanych efektów to powolna (około stopień na dzień) precesja orbity, o niewielkim wpływie na szukaną odpowiedź.
Z określenia układów wynika, że w momencie 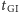 w układzie rakiety Warszawa miała położenie
w układzie rakiety Warszawa miała położenie 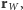 ale potem w czasie
ale potem w czasie 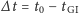 obróciła się wraz z Ziemią o kąt
obróciła się wraz z Ziemią o kąt 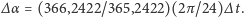 Licząc kąt obrotu, zamieniliśmy jednostki czasu na radiany i uwzględniliśmy, że dni liczymy względem obracającego się kierunku Ziemia-Słońce, czyli w ciągu roku Ziemia wykonuje o jeden obrót więcej niż liczba dni. Przy tym obrocie współrzędna
Licząc kąt obrotu, zamieniliśmy jednostki czasu na radiany i uwzględniliśmy, że dni liczymy względem obracającego się kierunku Ziemia-Słońce, czyli w ciągu roku Ziemia wykonuje o jeden obrót więcej niż liczba dni. Przy tym obrocie współrzędna 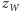 pozostaje bez zmiany, a współrzędne
pozostaje bez zmiany, a współrzędne 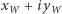 przekształcają się w następujący sposób:
przekształcają się w następujący sposób:

Znaleźliśmy zatem przedstawienia wszystkich wektorów w nierotującym układzie GI. Astronomowie zwykle używają nierotującego układu, w którym punkt Barana 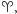 czyli przecięcie ekliptyki z równikiem, wyznacza oś
czyli przecięcie ekliptyki z równikiem, wyznacza oś 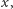 ale to temat na inną okazję.
ale to temat na inną okazję.
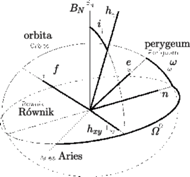
Elementy keplerowskie orbity
W artykule o prawach Keplera (Delta 5/2011) pokazaliśmy, jak z nich wyprowadzić drugie prawo dynamiki Newtona. Przy okazji zdobyliśmy wiedzę, która pozwoli nam opisać orbitę satelity.
Choć na razie nie znamy położenia orbity, to zaczniemy przekształcenia w układzie ze środkiem w centrum Ziemi, w którym oś  wskazuje perigeum, a oś
wskazuje perigeum, a oś 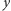 też leży w płaszczyźnie orbity. Obliczymy analitycznie rozmaite iloczyny wektorów
też leży w płaszczyźnie orbity. Obliczymy analitycznie rozmaite iloczyny wektorów 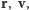 by na podstawie wyników zrozumieć ich związek z elementami orbity. Na końcu wrócimy do znanego nam układu GI i wykonamy te same obliczenia liczbowo, i korzystając z tego, że te iloczyny mają to samo znaczenie w każdym układzie, znajdziemy wartości elementów orbity. Jak to wyprowadziliśmy poprzednio, chwilowe położenie i prędkość na orbicie można wyrazić poprzez kąt zwany anomalią mimośrodową
by na podstawie wyników zrozumieć ich związek z elementami orbity. Na końcu wrócimy do znanego nam układu GI i wykonamy te same obliczenia liczbowo, i korzystając z tego, że te iloczyny mają to samo znaczenie w każdym układzie, znajdziemy wartości elementów orbity. Jak to wyprowadziliśmy poprzednio, chwilowe położenie i prędkość na orbicie można wyrazić poprzez kąt zwany anomalią mimośrodową 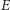 :
:
Aktualną wartość 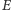 w chwili
w chwili 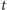 znajdujemy jako rozwiązanie równania Keplera:
znajdujemy jako rozwiązanie równania Keplera:
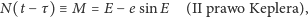 |
(3) |
gdzie 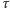 jest czasem przejścia przez perigeum, a
jest czasem przejścia przez perigeum, a

zwane ruchem średnim w istocie jest uśrednioną prędkością kątową satelity, natomiast 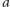 i
i  oznaczają odpowiednio półoś wielką orbity (połowę odległości między perigeum i apogeum) oraz mimośród (spłaszczenie) orbity. Dla skrócenia zapisu wprowadziliśmy
oznaczają odpowiednio półoś wielką orbity (połowę odległości między perigeum i apogeum) oraz mimośród (spłaszczenie) orbity. Dla skrócenia zapisu wprowadziliśmy 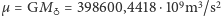 zamiast iloczynu stałej grawitacji i masy Ziemi.
zamiast iloczynu stałej grawitacji i masy Ziemi.
Chociaż obliczenia prowadzimy w układzie płaszczyzny orbity, to będziemy korzystać wyłącznie z iloczynów wektorów, aby wynik przedstawić w postaci niezależnej od wyboru układu współrzędnych. Kwadraty długości wektorów mamy z twierdzenia Pitagorasa lub z iloczynu skalarnego wektora przez siebie, co na jedno wychodzi:
gdzie ostatnia równość wynika z podstawienia (4) do (5). Z ostatniego wzoru wynika, że energia całkowita 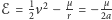 jest stała, jak należało oczekiwać, oraz:
jest stała, jak należało oczekiwać, oraz:

Mając półoś  orbity, spłaszczenie orbity znajdziemy z pomocą iloczynu skalarnego (1) przez (2):
orbity, spłaszczenie orbity znajdziemy z pomocą iloczynu skalarnego (1) przez (2):
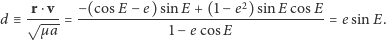 |
(6) |
Korzystając z (4) oraz (6), mamy

Tak znalezione  i
i 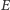 po podstawieniu do (3) dają
po podstawieniu do (3) dają 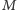 oraz czas
oraz czas 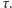 Ćwiartkę, do której należy kąt
Ćwiartkę, do której należy kąt 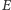 (i podobnie dla innych kątów), określamy na podstawie znaków funkcji
(i podobnie dla innych kątów), określamy na podstawie znaków funkcji 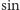 i
i 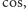 natomiast wartość samego kąta wyznaczymy za pomocą funkcji
natomiast wartość samego kąta wyznaczymy za pomocą funkcji 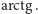
Gdy 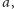
 i
i 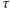 są znane, to pozostaje wyznaczyć trzy elementy określające orientację orbity w przestrzeni. Dwa z nich to kąty
są znane, to pozostaje wyznaczyć trzy elementy określające orientację orbity w przestrzeni. Dwa z nich to kąty 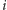 oraz
oraz 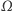 wskazujące kierunek wektora momentu pędu
wskazujące kierunek wektora momentu pędu 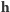 w układzie współrzędnych, w którym oś
w układzie współrzędnych, w którym oś  pokrywa się z osią obrotu Ziemi. Moment pędu jest proporcjonalny do iloczynu wektorowego
pokrywa się z osią obrotu Ziemi. Moment pędu jest proporcjonalny do iloczynu wektorowego  i
i 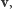 który w układzie współrzędnych o osiach
który w układzie współrzędnych o osiach 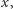
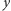 leżących w płaszczyźnie orbity ma postać:
leżących w płaszczyźnie orbity ma postać:
Zasada zachowania pędu zapewnia, że 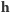 w nieobracającym się układzie jest stałe. Znajdziemy teraz współrzędne wektora
w nieobracającym się układzie jest stałe. Znajdziemy teraz współrzędne wektora 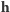 w układzie współrzędnych, którego oś
w układzie współrzędnych, którego oś  pokrywa się z osią obrotu Ziemi. W tym układzie współrzędnych, składowa tego wektora w płaszczyźnie
pokrywa się z osią obrotu Ziemi. W tym układzie współrzędnych, składowa tego wektora w płaszczyźnie 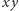 to
to 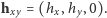 Nachylenie
Nachylenie 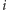 wektora
wektora 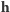 do osi
do osi  oraz nachylenie
oraz nachylenie 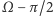 wektora
wektora 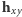 do osi
do osi 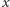 wynikają ze stosunku ich składowych:
wynikają ze stosunku ich składowych:

Sam kąt 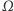 to kąt w płaszczyźnie
to kąt w płaszczyźnie 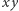 między osią
między osią  a prostopadłym do
a prostopadłym do 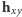 wektorem
wektorem

wskazującym linię węzłów, tj. linię przecięcia orbity z płaszczyzną 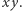
Powróćmy do układu płaszczyzny orbity. Zanim wyznaczymy położenie perigeum, znajdźmy pomocniczy wektor, mnożąc wektorowo (2) oraz (7):

Następnie odejmując (1) podzielone przez (4), otrzymujemy

Tak zdefiniowany wektor mimośrodowy ma długość  i wskazuje kierunek perigeum. Wektory
i wskazuje kierunek perigeum. Wektory 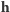 i
i  całkowicie określają orientację orbity. Prostopadły do
całkowicie określają orientację orbity. Prostopadły do  wektor
wektor

też leży w płaszczyźnie orbity. Zatem iloczyny skalarne 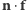 i
i 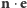 są proporcjonalne do sinusa i kosinusa kąta
są proporcjonalne do sinusa i kosinusa kąta 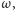 jaki kierunek perihelium tworzy z linią węzłów, skąd:
jaki kierunek perihelium tworzy z linią węzłów, skąd:

gdzie minus uwzględnia, że kąt względem 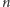 t.j.
t.j. 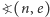 a nie względem
a nie względem 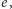
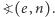 Kąty nachylenie
Kąty nachylenie 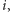 argument perigeum
argument perigeum 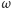 i długość linii węzłów
i długość linii węzłów 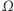 w pełni określają położenie orbity. Ponieważ wszystkie elementy określiliśmy za pomocą iloczynów wektorów, to wzory pozostają słuszne po dowolnym obrocie orbity, zmienią się tylko składowe wektorów, ale nie ich długości i kąty między nimi. Zatem do powyższych iloczynów wektorowych można teraz podstawić znane wektory w układzie GI, by otrzymać elementy orbity i wektory pomocnicze w tym właśnie układzie.
w pełni określają położenie orbity. Ponieważ wszystkie elementy określiliśmy za pomocą iloczynów wektorów, to wzory pozostają słuszne po dowolnym obrocie orbity, zmienią się tylko składowe wektorów, ale nie ich długości i kąty między nimi. Zatem do powyższych iloczynów wektorowych można teraz podstawić znane wektory w układzie GI, by otrzymać elementy orbity i wektory pomocnicze w tym właśnie układzie.
Widoczność w Warszawie
Teraz możemy opisać sposób znalezienia odpowiedzi na pytanie postawione na samym początku. Dla nowego momentu czasu 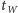 należy obliczyć
należy obliczyć 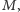 następnie rozwiązać (3) na
następnie rozwiązać (3) na 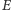 i znaleźć
i znaleźć  w płaszczyźnie orbity z (1). Wtedy w układzie GI położenie będzie równe
w płaszczyźnie orbity z (1). Wtedy w układzie GI położenie będzie równe 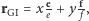 gdzie wektory
gdzie wektory  i
i 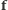 określają kierunki dużej i małej osi orbity. Dalej, oznaczając położenie Warszawy przez
określają kierunki dużej i małej osi orbity. Dalej, oznaczając położenie Warszawy przez 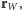 możemy wyrazić wektor wodzący z Warszawy do satelity jako
możemy wyrazić wektor wodzący z Warszawy do satelity jako 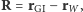 a kosinus kąta między zenitem a satelitą, pomijając spłaszczenie Ziemi, wynosi:
a kosinus kąta między zenitem a satelitą, pomijając spłaszczenie Ziemi, wynosi:

Dokończenie rachunków i znalezienie ostatecznej odpowiedzi na postawione na początku artykułu pytanie pozostawiamy Czytelnikowi.
Zainteresowani Czytelnicy mogą także wykonać obliczenia dla swojego położenia i w dowolnej chwili, korzystając z danych TLE BRITE-PL Lem publikowanych przez NORAD. Są one podane w nierotującym układzie względem punktu 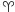 w płaszczyźnie
w płaszczyźnie 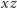 (rektascencja i deklinacja). Pozycję
(rektascencja i deklinacja). Pozycję 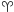 określa się na podstawie zliczenia dni juliańskich (JD) dla danej daty i obrotu Ziemi względem
określa się na podstawie zliczenia dni juliańskich (JD) dla danej daty i obrotu Ziemi względem 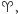 tj. czasu gwiazdowego w Greenwich. Przy tym na podstawie czasu, jaki upłynął od epoki TLE, warto uwzględnić precesję
tj. czasu gwiazdowego w Greenwich. Przy tym na podstawie czasu, jaki upłynął od epoki TLE, warto uwzględnić precesję 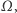 biorąc pod uwagę jej szybkość podaną w TLE jako
biorąc pod uwagę jej szybkość podaną w TLE jako