Wyznaczanie wysokości wzgórz na powierzchni Księżyca

Wikimedia Commons
Rys. 3
Cienie widoczne na tarczy Księżyca są cennym źródłem informacji o ukształtowaniu jego powierzchni. Widoczna z Ziemi długość cienia dowolnego wzniesienia zależy od fazy Księżyca. Największa jest wtedy, gdy w pobliżu nierówności, rzucającej cień, przebiega linia terminatora. Najbardziej „chropowaty” Księżyc zobaczymy wtedy, gdy jasna jest połowa tarczy, natomiast w czasie pełni jego powierzchnia wydaje się zupełnie płaska.
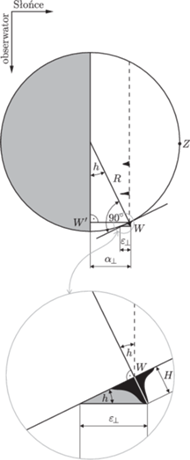
Rys. 1 Wzniesienie na powierzchni Księżyca i rzucany przez nie cień. Płaszczyznę rysunku
wyznaczają środki Słońca i Księżyca oraz położenie ziemskiego obserwatora. Wzniesienia
W, leżące na okręgu, którego płaszczyzna jest równoległa do płaszczyzny terminatora (linia
przerywana), są oświetlane przez Słońce pod tym samym kątem
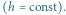

Rys. 2 Obserwowana kątowa długość odcinka
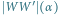 oraz długość cienia
oraz długość cienia
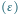 zależą od kąta
zależą od kąta
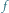 (czyli od fazy Księżyca). Okrąg narysowany linią
przerywaną jest śladem przecięcia z globem Księżyca płaszczyzny równoległej do płaszczyzny
rysunku i przechodzącej przez wzniesienie. Ślad ten dla ziemskiego obserwatora będzie
odcinkiem prostopadłym do prostej łączącej punkty kontaktu terminatora z brzegiem tarczy
Księżyca.
(czyli od fazy Księżyca). Okrąg narysowany linią
przerywaną jest śladem przecięcia z globem Księżyca płaszczyzny równoległej do płaszczyzny
rysunku i przechodzącej przez wzniesienie. Ślad ten dla ziemskiego obserwatora będzie
odcinkiem prostopadłym do prostej łączącej punkty kontaktu terminatora z brzegiem tarczy
Księżyca.
Zadanie postawione w tytule jest bardzo łatwe do rozwiązania w przypadku, gdy
widzimy dokładnie połowę tarczy Księżyca (Rys. 1). Załóżmy, że wzniesienie
W leży w płaszczyźnie wyznaczonej przez środki Słońca i Księżyca
oraz położenie ziemskiego obserwatora. Z trójkąta, w którym jedną
z przyprostokątnych jest wysokość wzgórza
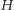 (patrz: powiększony
szczegół po prawej stronie rysunku 1), wynika, że
(patrz: powiększony
szczegół po prawej stronie rysunku 1), wynika, że
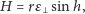 | (1) |
gdzie
 oznacza odległość Ziemia–Księżyc,
oznacza odległość Ziemia–Księżyc,
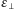 – obserwowaną
kątową długość cienia wzniesienia, zaś
– obserwowaną
kątową długość cienia wzniesienia, zaś
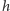 – kątową wysokość
Słońca ponad horyzontem w miejscu, w którym położone jest wzniesienie.
Symbole opatrzone „
– kątową wysokość
Słońca ponad horyzontem w miejscu, w którym położone jest wzniesienie.
Symbole opatrzone „
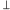 ” dotyczą chwili, gdy patrzymy na Księżyc
prostopadle do kierunku Księżyc–Słońce (gdy Księżyc jest w pierwszej lub
ostatniej kwadrze). Gdy
” dotyczą chwili, gdy patrzymy na Księżyc
prostopadle do kierunku Księżyc–Słońce (gdy Księżyc jest w pierwszej lub
ostatniej kwadrze). Gdy
 oznacza odległość Ziemia–Księżyc,
oznacza odległość Ziemia–Księżyc,
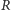 – promień Księżyca (w dalszych rozważaniach jego wartość
przyjmiemy za daną) i
– promień Księżyca (w dalszych rozważaniach jego wartość
przyjmiemy za daną) i
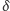 – kątowy promień jego tarczy, mamy
– kątowy promień jego tarczy, mamy
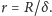 Wobec tego zależność (1) można zapisać w postaci:
Wobec tego zależność (1) można zapisać w postaci:

W omawianym przypadku wysokość Słońca ponad horyzontem
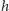 w miejscu, w którym znajduje się wzniesienie, jest łatwa do
wyznaczenia. Jest ona równa kątowi między płaszczyzną terminatora a prostą
łączącą środek Księżyca i wzniesienie. Skoro tak, to
w miejscu, w którym znajduje się wzniesienie, jest łatwa do
wyznaczenia. Jest ona równa kątowi między płaszczyzną terminatora a prostą
łączącą środek Księżyca i wzniesienie. Skoro tak, to

gdzie
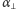 jest kątową odległością wzniesienia W od płaszczyzny
terminatora, czyli
jest kątową odległością wzniesienia W od płaszczyzny
terminatora, czyli
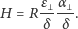 | (2) |
W przedstawionej sytuacji wyznaczenie wysokości wzniesienia wymagało
będzie zmierzenia kątowej średnicy tarczy Księżyca
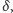 kątowej
długości cienia wzniesienia
kątowej
długości cienia wzniesienia
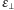 oraz kątowej odległości tego wzniesienia
od płaszczyzny terminatora
oraz kątowej odległości tego wzniesienia
od płaszczyzny terminatora
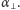
Otrzymane rozwiązanie dotyczy bardzo szczególnej chwili, gdy oświetlona jest
dokładnie połowa tarczy Księżyca, oraz szczególnej lokalizacji wzniesienia.
Wystarczy jednak chwila zastanowienia, by usunąć drugie z wymienionych
ograniczeń. Zauważmy bowiem, że płaszczyzna horyzontu jest w każdym
miejscu styczna do globu, czyli jest prostopadła do kierunku ku centrum globu
(patrz Rys. 1). Skoro tak, to wysokość
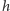 Słońca ponad horyzontem
w dowolnym miejscu globu jest równa kątowi między kierunkiem ku centrum
globu i płaszczyzną terminatora. Oznacza to, że ma ona jednakową wartość
we wszystkich miejscach globu, które są równoodlegle od płaszczyzny
terminatora. Punkty o jednakowej wartości
Słońca ponad horyzontem
w dowolnym miejscu globu jest równa kątowi między kierunkiem ku centrum
globu i płaszczyzną terminatora. Oznacza to, że ma ona jednakową wartość
we wszystkich miejscach globu, które są równoodlegle od płaszczyzny
terminatora. Punkty o jednakowej wartości
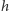 tworzą na powierzchni
Księżyca okręgi równoległe do płaszczyzny terminatora, których środki są
położone na prostej łączącej środki Księżyca i Słońca. Największym z tych
okręgów jest terminator, dla którego
tworzą na powierzchni
Księżyca okręgi równoległe do płaszczyzny terminatora, których środki są
położone na prostej łączącej środki Księżyca i Słońca. Największym z tych
okręgów jest terminator, dla którego
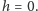 Kątowa wysokość
Słońca wzrasta ze wzrostem odległości od terminatora. W punkcie
Kątowa wysokość
Słońca wzrasta ze wzrostem odległości od terminatora. W punkcie
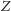 Słońce jest w zenicie. Zależność (2) można zatem stosować do
wyznaczania wysokości wzniesienia położonego w dowolnym miejscu tarczy,
lecz tylko wtedy, gdy Księżyc jest bliski pierwszej lub ostatniej kwadry.
Rozwiązanie (2) pozostaje jednak mało użyteczne ze względu na pierwsze
z wymienionych ograniczeń. Okresy, w których Księżyc położony jest
blisko prostokątnego narożnika trójkąta, są krótkie i mogą pokrywać się
z okresami niepogody. Nietrudno jest jednak otrzymać rozwiązanie
ogólniejsze. Jeśli licznik i mianownik zależności (2) pomnożymy przez
Słońce jest w zenicie. Zależność (2) można zatem stosować do
wyznaczania wysokości wzniesienia położonego w dowolnym miejscu tarczy,
lecz tylko wtedy, gdy Księżyc jest bliski pierwszej lub ostatniej kwadry.
Rozwiązanie (2) pozostaje jednak mało użyteczne ze względu na pierwsze
z wymienionych ograniczeń. Okresy, w których Księżyc położony jest
blisko prostokątnego narożnika trójkąta, są krótkie i mogą pokrywać się
z okresami niepogody. Nietrudno jest jednak otrzymać rozwiązanie
ogólniejsze. Jeśli licznik i mianownik zależności (2) pomnożymy przez
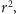 dostaniemy
dostaniemy

Iloczyny
 są odcinkami równoległymi do kierunku
Księżyc–Słońce. Gdy widzimy połowę tarczy Księżyca, to na odcinki te
patrzymy prostopadle. Przy innej fazie patrzymy na nie pod pewnym kątem
są odcinkami równoległymi do kierunku
Księżyc–Słońce. Gdy widzimy połowę tarczy Księżyca, to na odcinki te
patrzymy prostopadle. Przy innej fazie patrzymy na nie pod pewnym kątem
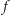 (wartości
(wartości
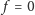 odpowiada pierwsza kwadra,
odpowiada pierwsza kwadra,
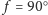 –
pełnia,
–
pełnia,
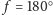 – ostatnia kwadra,
– ostatnia kwadra,
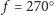 – nów). Rysunek 2
przedstawia sytuację, gdy Księżyc jest w fazie między pierwszą kwadrą i pełnią.
Wynika z niego następująca zależność między długością odcinków
– nów). Rysunek 2
przedstawia sytuację, gdy Księżyc jest w fazie między pierwszą kwadrą i pełnią.
Wynika z niego następująca zależność między długością odcinków
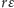 i
i
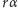 oraz
oraz
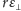 i
i
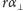 :
:

Zależności te pozwalają uogólnić wzór (2) dla dowolnej fazy Księżyca:
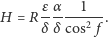 | (3) |
Widać, że zależność wysokości wzgórza
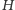 od kąta
od kąta
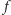 jest
słaba dla niewielkich jego wartości. Przyjmijmy np., że
jest
słaba dla niewielkich jego wartości. Przyjmijmy np., że
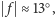 co
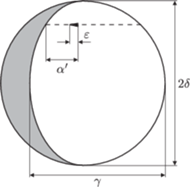
odpowiada odstępowi około 1 doby od pierwszej lub ostatniej kwadry. Kształt
jasnej części Księżyca, odpowiadający tym chwilom, jest pokazany na
rysunku 3 Użycie zależności (2) zamiast (3) jest wtedy źródłem
błędu względnego rzędu
co
odpowiada odstępowi około 1 doby od pierwszej lub ostatniej kwadry. Kształt
jasnej części Księżyca, odpowiadający tym chwilom, jest pokazany na
rysunku 3 Użycie zależności (2) zamiast (3) jest wtedy źródłem
błędu względnego rzędu
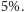 Tymczasem rozmycie granicy cienia
i linii terminatora skutkuje dużymi błędami pomiaru kątów
Tymczasem rozmycie granicy cienia
i linii terminatora skutkuje dużymi błędami pomiaru kątów
 i
i
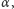 czego finalnym skutkiem jest względny błąd wartości
czego finalnym skutkiem jest względny błąd wartości
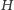 nie
mniejszy niż
nie
mniejszy niż
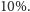 Wynika stąd, że do wyznaczania wysokości
wzniesień w chwilach bliskich momentowi, gdy widoczna jest połowa tarczy
Księżyca, można wykorzystywać zależność (2).
Wynika stąd, że do wyznaczania wysokości
wzniesień w chwilach bliskich momentowi, gdy widoczna jest połowa tarczy
Księżyca, można wykorzystywać zależność (2).

Rys. 3
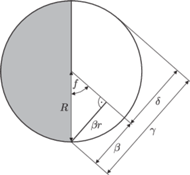
Rys. 4 Kąt
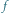 można wyznaczyć, mierząc kąty
można wyznaczyć, mierząc kąty
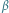 i
i
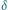 bądź
bądź
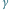 i
i
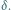
Jeśli kształt jasnej części Księżyca będzie wyraźnie różnił się od połowy
okręgu, to na podstawie rysunku 4 możemy sformułować zależność
umożliwiającą wyznaczenie wartości kąta
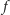 i uwzględnienie jej
w zależności (3)
i uwzględnienie jej
w zależności (3)

Tak więc dla dowolnej fazy Księżyca (dowolnej wartości kąta
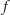 )
zależność (3) wygląda następująco:
)
zależność (3) wygląda następująco:

Ponieważ w praktyce znacznie łatwiej można zmierzyć kąt
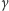 niż
niż
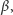 zależność powyższą – pamiętając, że
zależność powyższą – pamiętając, że
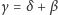 –
możemy zapisać jako funkcję kąta
–
możemy zapisać jako funkcję kąta
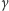 :
:
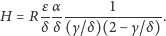 | (4) |
Krótkiego komentarza wymaga jeszcze problem pomiaru kąta
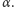 Jak wynika
z rysunku 2, jest to kąt, pod jakim widoczny jest odcinek
Jak wynika
z rysunku 2, jest to kąt, pod jakim widoczny jest odcinek
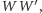 gdzie
gdzie
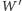 jest rzutem punktu
jest rzutem punktu
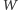 na płaszczyznę terminatora
(punkt
na płaszczyznę terminatora
(punkt
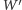 jest położony pod powierzchnią Księżyca). Dokładny
pomiar tego kąta nie jest więc możliwy poza szczególnym przypadkiem,
gdy widoczna jest dokładnie połowa tarczy Księżyca. Wtedy bowiem
punkt
jest położony pod powierzchnią Księżyca). Dokładny
pomiar tego kąta nie jest więc możliwy poza szczególnym przypadkiem,
gdy widoczna jest dokładnie połowa tarczy Księżyca. Wtedy bowiem
punkt
 będzie położony dokładnie na linii terminatora, tzn.
będzie położony dokładnie na linii terminatora, tzn.
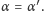 Jeżeli obserwacji dokonano w chwili bliskiej momentowi
wystąpienia pierwszej lub ostatniej kwadry, to punkt
Jeżeli obserwacji dokonano w chwili bliskiej momentowi
wystąpienia pierwszej lub ostatniej kwadry, to punkt
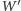 będzie znajdował
się bardzo blisko terminatora, w odległości niewiele większej niż nieostrość
jego granicy. Możemy wtedy przyjąć, że
będzie znajdował
się bardzo blisko terminatora, w odległości niewiele większej niż nieostrość
jego granicy. Możemy wtedy przyjąć, że
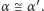 Zauważmy jednak,
że również dla dowolnej fazy Księżyca problem określenia wartości
Zauważmy jednak,
że również dla dowolnej fazy Księżyca problem określenia wartości
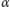 rozwiązuje się sam. Cienie wzgórz dostatecznie długie, by można było
mierzyć je w miarę dokładnie, są widoczne tylko blisko terminatora,
a wtedy punkt
rozwiązuje się sam. Cienie wzgórz dostatecznie długie, by można było
mierzyć je w miarę dokładnie, są widoczne tylko blisko terminatora,
a wtedy punkt
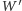 również będzie bardzo blisko linii terminatora.
Skoro tak, to niezależnie od fazy Księżyca możemy przyjmować, że
również będzie bardzo blisko linii terminatora.
Skoro tak, to niezależnie od fazy Księżyca możemy przyjmować, że
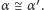
Przyglądając się zależności (4), będącej rozwiązaniem postawionego zadania, warto zauważyć, że wielkości kątowe występują w niej wyłącznie w postaci ilorazów.
Rys. 5 Kąty, które należy zmierzyć, aby wyznaczyć wysokość wzniesienia. Linia przerywana łączy punkty jednakowo odległe od płaszczyzny wyznaczonej przez położenie obserwatora, środka Księżyca i środka Słońca.
Dzięki temu do wyznaczenia wysokości wzniesienia nie jest potrzebna znajomość kątowej skali obrazu Księżyca obserwowanego w lunecie bądź kątowej skali fotografii Księżyca. Otrzymane zależności są, oczywiście, prawdziwe dla dowolnego kulistego obiektu oświetlonego odległym, niemal punktowym źródłem światła.
* * *
Jeśli
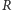 uznamy za wielkość znaną, to do wyznaczenia wysokości
wzniesienia konieczne będzie zmierzenie czterech kątów:
uznamy za wielkość znaną, to do wyznaczenia wysokości
wzniesienia konieczne będzie zmierzenie czterech kątów:
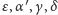 (Rys. 5).
Można je zmierzyć w trakcie bezpośredniej obserwacji wizualnej lub
wykorzystując do pomiarów zdjęcie Księżyca.
(Rys. 5).
Można je zmierzyć w trakcie bezpośredniej obserwacji wizualnej lub
wykorzystując do pomiarów zdjęcie Księżyca.
Zrobienie zdjęcia Księżyca, umożliwiającego wykonanie niezbędnych pomiarów z rozsądną dokładnością, wymaga użycia obiektywu o ogniskowej zbliżonej do 1 m. Rolę takiego obiektywu spełnia zazwyczaj obiektyw lunety lub zwierciadło teleskopu. Decydujący wpływ na dokładność pomiaru ma wielkość i ostrość obrazu Księżyca. Ze względu na drgania układu fotografującego powodowane powiewami wiatru i turbulencją atmosferyczną czas naświetlania nie powinien przekraczać 1/30 sekundy. Ponieważ jedną z mierzonych wielkości jest promień tarczy Księżyca, a wielkość tę można wyznaczyć najdokładniej, mierząc średnicę tarczy, zdjęcie powinno obejmować całą oświetloną część tarczy.
Bezpośredni (wizualny) pomiar kątów
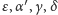 będzie wymagał
użycia lunety lub teleskopu umożliwiającego osiągnięcie ponad stokrotnego
powiększenia. Typując wzniesienia przewidziane do pomiaru, należy wybierać
takie, których otoczenie wydaje się w miarę płaskie i poziome. Jedyną
wskazówką, umożliwiającą ocenę stopnia spełnienia tego warunku, jest
światłocieniowy obraz otoczenia. Jeśli zależy nam na zmierzeniu wysokości
konkretnego wzniesienia, należy poczekać na wieczór, w którym znajdzie się
ono w pobliżu terminatora.
będzie wymagał
użycia lunety lub teleskopu umożliwiającego osiągnięcie ponad stokrotnego
powiększenia. Typując wzniesienia przewidziane do pomiaru, należy wybierać
takie, których otoczenie wydaje się w miarę płaskie i poziome. Jedyną
wskazówką, umożliwiającą ocenę stopnia spełnienia tego warunku, jest
światłocieniowy obraz otoczenia. Jeśli zależy nam na zmierzeniu wysokości
konkretnego wzniesienia, należy poczekać na wieczór, w którym znajdzie się
ono w pobliżu terminatora.
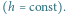
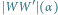 oraz długość cienia
oraz długość cienia
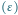 zależą od kąta
zależą od kąta
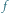 (czyli od fazy Księżyca). Okrąg narysowany linią
przerywaną jest śladem przecięcia z globem Księżyca płaszczyzny równoległej do płaszczyzny
rysunku i przechodzącej przez wzniesienie. Ślad ten dla ziemskiego obserwatora będzie
odcinkiem prostopadłym do prostej łączącej punkty kontaktu terminatora z brzegiem tarczy
Księżyca.
(czyli od fazy Księżyca). Okrąg narysowany linią
przerywaną jest śladem przecięcia z globem Księżyca płaszczyzny równoległej do płaszczyzny
rysunku i przechodzącej przez wzniesienie. Ślad ten dla ziemskiego obserwatora będzie
odcinkiem prostopadłym do prostej łączącej punkty kontaktu terminatora z brzegiem tarczy
Księżyca.
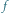 można wyznaczyć, mierząc kąty
można wyznaczyć, mierząc kąty
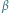 i
i
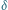 bądź
bądź
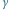 i
i