Klub 44M - zadania XII 2018»Zadanie 771
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania XII 2018
- Publikacja w Delcie: grudzień 2018
- Publikacja elektroniczna: 30 listopada 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (86 KB)
Wyznaczyć wszystkie funkcje różniczkowalne 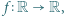 spełniające równanie
spełniające równanie
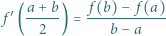
dla każdej pary różnych liczb rzeczywistych 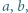 których różnica jest liczbą całkowitą.
których różnica jest liczbą całkowitą.
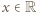 uzyskujemy z podanego równania (po podstawieniu
uzyskujemy z podanego równania (po podstawieniu 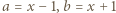 ) równość
) równość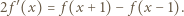
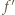 jest różniczkowalna. Możemy więc zróżniczkować (1) stronami, otrzymując
jest różniczkowalna. Możemy więc zróżniczkować (1) stronami, otrzymując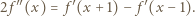
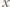 przez
przez 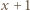 oraz
oraz 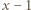 :
: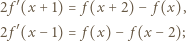
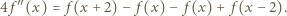
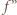 ma pochodną. Różniczkujemy (3) stronami:
ma pochodną. Różniczkujemy (3) stronami: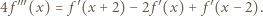
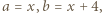 następnie
następnie 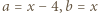 i wreszcie
i wreszcie 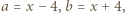 otrzymując kolejno
otrzymując kolejno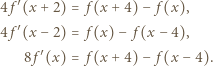
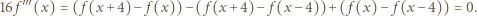
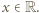 To znaczy, że
To znaczy, że 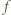 jest wielomianem stopnia najwyżej drugiego.
jest wielomianem stopnia najwyżej drugiego.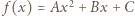 spełnia równanie dane w założeniu zadania (i to nawet dla każdej pary różnych liczb
spełnia równanie dane w założeniu zadania (i to nawet dla każdej pary różnych liczb 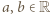 ) - co łatwo sprawdzić.
) - co łatwo sprawdzić.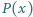 będzie takim wielomianem o współczynnikach rzeczywistych, że
będzie takim wielomianem o współczynnikach rzeczywistych, że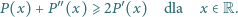
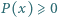 dla
dla 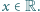
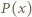 jest funkcją stałą, implikacja jest oczywista. Dalej przyjmijmy, że
jest funkcją stałą, implikacja jest oczywista. Dalej przyjmijmy, że 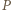 jest wielomianem stopnia dodatniego. Wielomian
jest wielomianem stopnia dodatniego. Wielomian 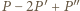 ma taki sam stopień, a przy tym przyjmuje - zgodnie z założeniem - wyłącznie wartości nieujemne. Jest to więc wielomian stopnia parzystego. Ten sam stopień ma zarówno wielomian
ma taki sam stopień, a przy tym przyjmuje - zgodnie z założeniem - wyłącznie wartości nieujemne. Jest to więc wielomian stopnia parzystego. Ten sam stopień ma zarówno wielomian 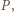 jak i wielomian
jak i wielomian 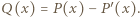 Każdy z tych wielomianów, jako funkcja ciągła zmiennej rzeczywistej, mająca granicę
Każdy z tych wielomianów, jako funkcja ciągła zmiennej rzeczywistej, mająca granicę  przy
przy  przyjmuje w pewnym punkcie osi liczbowej swoją wartość minimalną. Niech więc
przyjmuje w pewnym punkcie osi liczbowej swoją wartość minimalną. Niech więc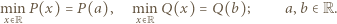
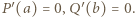 Zauważmy, że, w myśl założenia zadania,
Zauważmy, że, w myśl założenia zadania,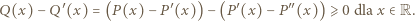
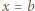 dostajemy
dostajemy 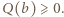 Jest to wartość minimalna wielomianu
Jest to wartość minimalna wielomianu 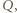 zatem
zatem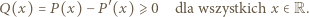
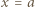 i mamy
i mamy 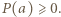 To wartość minimalna wielomianu
To wartość minimalna wielomianu 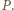 Zatem
Zatem 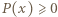 dla
dla 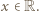
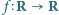 spełnia wraz z pewną funkcją
spełnia wraz z pewną funkcją 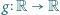 równanie
równanie 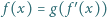 dla
dla 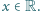 Dowieść, że funkcja
Dowieść, że funkcja 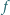 jest wypukła lub wklęsła.
jest wypukła lub wklęsła.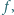 będąca różnowartościowym odwzorowaniem zbioru wszystkich liczb dodatnich na ten sam zbiór, i taka, że jej pochodna jest funkcją odwrotną do
będąca różnowartościowym odwzorowaniem zbioru wszystkich liczb dodatnich na ten sam zbiór, i taka, że jej pochodna jest funkcją odwrotną do 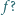
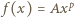 (motywacja: zarówno pochodna, jak i funkcja odwrotna do takiej funkcji, też ma taką postać - próba ma szansę powodzenia). Gdy stałe
(motywacja: zarówno pochodna, jak i funkcja odwrotna do takiej funkcji, też ma taką postać - próba ma szansę powodzenia). Gdy stałe 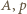 są dodatnie, funkcja
są dodatnie, funkcja 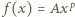 jest ściśle rosnąca i przekształca przedział
jest ściśle rosnąca i przekształca przedział 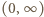 na ten sam przedział. Dla ustalonej wartości
na ten sam przedział. Dla ustalonej wartości 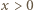 rozwiązujemy równanie
rozwiązujemy równanie 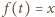 (z niewiadomą
(z niewiadomą 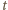 ), otrzymując
), otrzymując 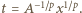 Tak więc
Tak więc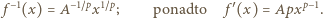
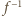 i
i 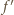 były identyczne, wystarczy, by parametry dodatnie
były identyczne, wystarczy, by parametry dodatnie 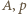 spełniały równania
spełniały równania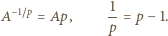
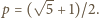 Dla tej stałej
Dla tej stałej 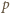 pierwsze równanie przybiera formę
pierwsze równanie przybiera formę 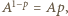 z rozwiązaniem
z rozwiązaniem 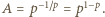 Funkcja
Funkcja 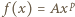 z tymi parametrami ma wymaganą własność.
z tymi parametrami ma wymaganą własność.
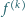 oznacza
oznacza 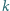 -tą pochodną
-tą pochodną 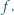 Czy
Czy 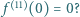
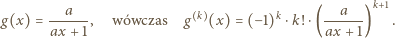
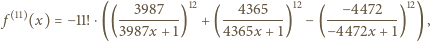
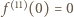 równoważny jest warunkowi
równoważny jest warunkowi 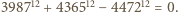 To zaś jest niemożliwe na mocy Wielkie Twierdzenie Fermata.
To zaś jest niemożliwe na mocy Wielkie Twierdzenie Fermata.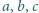 jest nie mniejsza od
jest nie mniejsza od
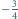 oraz
oraz
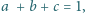 to
to

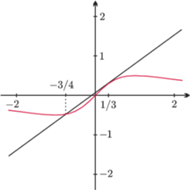
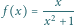
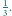
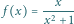
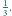
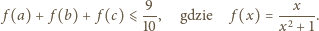
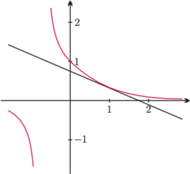
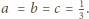 Równanie
stycznej do funkcji
Równanie
stycznej do funkcji
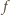 w punkcie
w punkcie
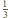 ma postać
ma postać
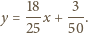
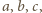 spełniających warunek
spełniających warunek
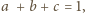 suma wartości wyrażenia
suma wartości wyrażenia
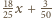 jest równa
jest równa
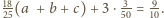
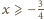 prawdziwa jest
nierówność
prawdziwa jest
nierówność
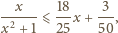
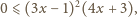
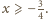
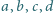 zachodzi
nierówność
zachodzi
nierówność

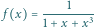
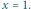
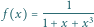
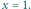
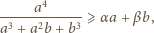
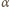 i
i
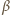 są pewnymi liczbami rzeczywistymi. Dzieląc obie
strony przez
są pewnymi liczbami rzeczywistymi. Dzieląc obie
strony przez
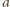 i podstawiając
i podstawiając
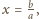 otrzymujemy
otrzymujemy
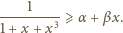
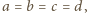 więc musimy tak dobrać współczynniki
więc musimy tak dobrać współczynniki
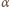 i
i
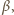 aby równość zachodziła dla
aby równość zachodziła dla
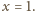 Znajdując
równanie stycznej do wykresu funkcji
Znajdując
równanie stycznej do wykresu funkcji
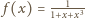 w punkcie
w punkcie
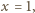 otrzymujemy współczynniki
otrzymujemy współczynniki
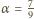 i
i
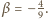
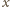 zachodzi
nierówność
zachodzi
nierówność
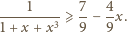
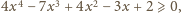 a następnie
doprowadzamy nierówność do postaci
a następnie
doprowadzamy nierówność do postaci
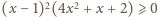 – teraz
widać, że to prawda dla dowolnego
– teraz
widać, że to prawda dla dowolnego
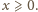
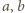 zachodzi nierówność
zachodzi nierówność
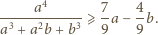
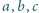 zachodzi
nierówność
zachodzi
nierówność

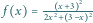
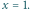
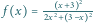
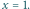
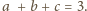 (Jest to bardziej wygodne niż założenie
(Jest to bardziej wygodne niż założenie
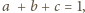 gdyż
równość zachodzi dla
gdyż
równość zachodzi dla
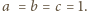 ) Wówczas dana nierówność
przyjmuje postać
) Wówczas dana nierówność
przyjmuje postać
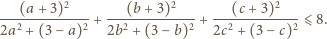
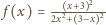 w punkcie
w punkcie
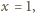 otrzymujemy do udowodnienia nierówność
otrzymujemy do udowodnienia nierówność
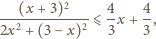
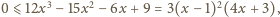 co
jest prawdą dla
co
jest prawdą dla
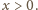
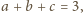 nierówność
zachodzi nie tylko dla liczb dodatnich, ale także dla nie mniejszych niż
nierówność
zachodzi nie tylko dla liczb dodatnich, ale także dla nie mniejszych niż
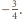
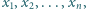 gdzie
gdzie
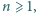 spełniają warunki
spełniają warunki

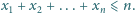
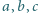 zachodzi
nierówność
zachodzi
nierówność

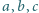 zachodzi
nierówność
zachodzi
nierówność

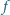 będzie funkcją o wartościach rzeczywistych, określoną na
zbiorze liczb dodatnich, dwukrotnie różniczkowalną, spełniającą warunek
będzie funkcją o wartościach rzeczywistych, określoną na
zbiorze liczb dodatnich, dwukrotnie różniczkowalną, spełniającą warunek
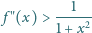 dla
dla
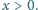 Czy taka funkcja może mieć asymptotę
przy
Czy taka funkcja może mieć asymptotę
przy
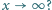
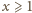 zachodzi nierówność
zachodzi nierówność
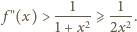
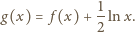
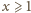 mamy
mamy
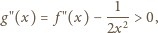
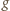 jest ściśle wypukła w przedziale
jest ściśle wypukła w przedziale
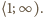 Stąd
wynika, że dla każdej liczby
Stąd
wynika, że dla każdej liczby
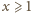 jest spełniona nierówność
jest spełniona nierówność
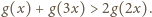 Po podstawieniu wyrażenia definiującego
funkcję
Po podstawieniu wyrażenia definiującego
funkcję
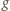 i prostym przekształceniu dostajemy:
i prostym przekształceniu dostajemy:
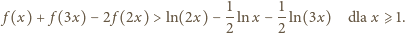
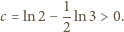
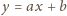 jest asymptotą funkcji
jest asymptotą funkcji
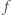 przy
przy
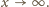 To znaczy, że
To znaczy, że
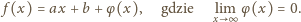
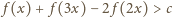
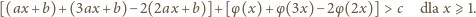
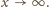 Wniosek: Funkcja
Wniosek: Funkcja
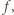 spełniająca podane warunki, nie ma
asymptoty przy
spełniająca podane warunki, nie ma
asymptoty przy
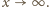
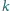 będzie liczbą naturalną większą od 1. Dla jakich dodatnich liczb
rzeczywistych
będzie liczbą naturalną większą od 1. Dla jakich dodatnich liczb
rzeczywistych
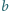 można znaleźć funkcję
można znaleźć funkcję
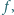 ciągłą na przedziale
ciągłą na przedziale
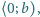 różniczkowalną wewnątrz tego przedziału oraz spełniającą
warunki:
różniczkowalną wewnątrz tego przedziału oraz spełniającą
warunki:
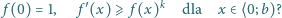
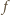 będzie funkcją, spełniającą podane warunki. Zauważmy, że
będzie funkcją, spełniającą podane warunki. Zauważmy, że
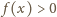 w przedziale
w przedziale
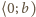 (w przeciwnym razie, oznaczając przez
(w przeciwnym razie, oznaczając przez
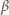 najmniejsze miejsce zerowe funkcji
najmniejsze miejsce zerowe funkcji
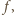 mielibyśmy w przedziale
mielibyśmy w przedziale
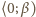 nierówności
nierówności
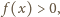
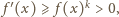 skąd
skąd
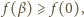 czyli
czyli
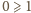 ).
).
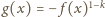 z pochodną
z pochodną
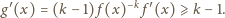
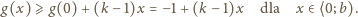
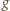 w przedziale
w przedziale
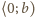 są ujemne. Tak więc
są ujemne. Tak więc
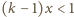 dla wszystkich
dla wszystkich
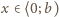 ; to znaczy, że liczba
; to znaczy, że liczba
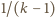 nie należy do tego przedziału – czyli zachodzi nierówność
nie należy do tego przedziału – czyli zachodzi nierówność
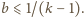 Na odwrót, jeżeli
Na odwrót, jeżeli
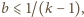 to określamy
funkcję
to określamy
funkcję
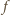 wzorem
wzorem
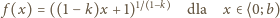
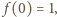
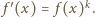 Stąd
odpowiedź: liczby
Stąd
odpowiedź: liczby
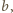 o które pyta zadanie, są scharakteryzowane
nierównością
o które pyta zadanie, są scharakteryzowane
nierównością
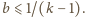
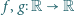 ,
mających pochodne wszystkich rzędów i spełniających warunki:
,
mających pochodne wszystkich rzędów i spełniających warunki:
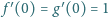 oraz
oraz
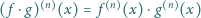
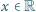 ,
,