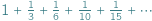Delta mi!

Każdy, komu choć raz zdarzyło się grać na gitarze lub innym instrumencie strunowym, dobrze wie, że na wysokość dźwięku ma wpływ między innymi długość struny. Uderzając w struny zbudowane z tego samego materiału i o tych samych grubościach, lecz o różnych długościach, otrzymamy dwie różne częstotliwości drgań, a więc dwa dźwięki o różnych wysokościach. A jak to jest z instrumentami perkusyjnymi? Czy na podstawie brzmienia drgającej membrany bębenka można powiedzieć coś o jego kształcie?

Wielomian jaki jest, każdy widzi. I każdy, kto widzi, wie również, że wielomiany miewają pierwiastki rzeczywiste (czyli miejsca zerowe), ale nie zawsze...

W marcu 1672 roku do Paryża przybył z misją dyplomatyczną od elektora mogunckiego młody prawnik, filozof i erudyta Gottfried Wilhelm Leibniz (1646-1716). Spotkanie z Christiaanem Huygensem (jesienią 1672 r.) przekonało Leibniza, że w matematyce jest nowicjuszem. Huygens, chcąc zbadać matematyczną przenikliwość Leibniza, rzucił mu takie oto wyzwanie: wyznaczyć sumę szeregu Leibniz zadanie wykonał (a Ty? rozwiązanie jest tutaj)...

Czytelnicy Delty zapewne znają zawody matematyczne dla uczniów, takie jak Olimpiada Matematyczna lub Kangur Matematyczny. Nie wszyscy wiedzą jednak, że konkursowe zmagania można kontynuować również podczas studiów. Na niektórych uczelniach odbywają się nawet specjalne zajęcia, podczas których rozwiązuje się i omawia zadania konkursowe.

Poniższe zadania łączy to, że do rozwiązania każdego z nich można użyć pewnego Bardzo Znanego Twierdzenia, udowodnionego całkiem niedawno. Oczywiście to, że można strzelać z armaty do muchy nie oznacza, że zawsze trzeba...

W dowodzeniu nierówności często pomocna bywa tak zwana metoda stycznych. Zdarza się, że wykres funkcji leży nad pewną prostą styczną do niego lub pod taką prostą (wszędzie lub tylko na jakimś przedziale). To oznacza, że możemy oszacować wartości tej funkcji przez wartości funkcji liniowej, której wykresem jest wybrana styczna. Żeby takie oszacowanie doprowadziło do celu, wybrana styczna musi przechodzić przez punkt, dla którego badana nierówność jest równością. Przyjrzymy się kilku przykładom zastosowań tej metody.

Jednym z fundamentalnych pojęć analizy matematycznej jest bez wątpienia różniczkowalność. Dla funkcji jednej zmiennej, określonej na pewnym otwartym przedziale, równoważna jest ona istnieniu pochodnej funkcji w każdym punkcie tego przedziału. Jak wiadomo, wszystkie funkcje elementarne są różniczkowalne w tym klasycznym sensie, jednak wiele innych prostych i zarazem użytecznych funkcji już nie.

W Delcie 10/2009, w artykule Czy naprawdę prawie robi wielką różnicę, Paulina Małolepsza i Tomasz Małolepszy piszą o przykładach funkcji ciągłych, które są różniczkowalne prawie wszędzie, ale jednak nie są całkami swoich pochodnych.