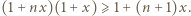U(nie)jednorodnianie nierówności»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu U(nie)jednorodnianie nierówności
- Publikacja w Delcie: lipiec 2020
- Publikacja elektroniczna: 1 lipca 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (400 KB)
Wykazać, że jeśli liczby 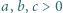 spełniają warunek
spełniają warunek 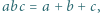 to
to 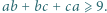
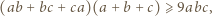
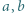 i
i  spełniają równość
spełniają równość 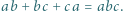 Dowieść, że
Dowieść, że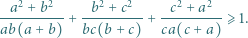
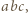 a prawą przez
a prawą przez 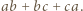 Następnie skorzystać z nierówności
Następnie skorzystać z nierówności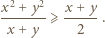
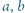 i
i  spełniają warunek
spełniają warunek 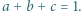 Dowieść, że
Dowieść, że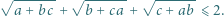
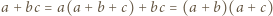 wraz z dwiema analogicznymi równościami. Wykorzystać nierówność
wraz z dwiema analogicznymi równościami. Wykorzystać nierówność 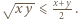
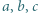 jest równy 1, to
jest równy 1, to 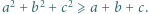
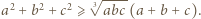 Można to zrobić, dodając stronami nierówność między średnią arytmetyczną i geometryczną
Można to zrobić, dodając stronami nierówność między średnią arytmetyczną i geometryczną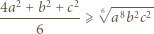
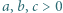 prawdziwa jest nierówność
prawdziwa jest nierówność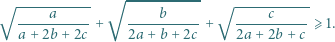
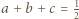 i udowodnić, że
i udowodnić, że 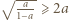 dla
dla 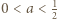 oraz analogicznie dla
oraz analogicznie dla 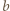 i
i 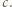
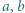 i
i  oraz liczby całkowitej
oraz liczby całkowitej 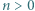 zachodzi nierówność
zachodzi nierówność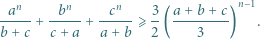
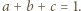 Wtedy
Wtedy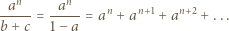
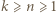 z nierówności
z nierówności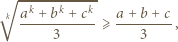
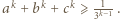 Tę ostatnią nierówność wystarczy zsumować dla
Tę ostatnią nierówność wystarczy zsumować dla 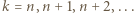
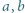 i
i  oraz liczby całkowitej
oraz liczby całkowitej 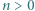 zachodzi nierówność
zachodzi nierówność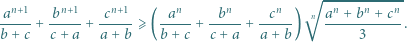
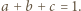 Posługując się nierównościami między średnimi potęgowymi, wykazać dla
Posługując się nierównościami między średnimi potęgowymi, wykazać dla 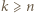 nierówności
nierówności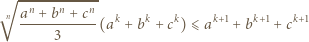
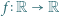 spełniające dla wszystkich
spełniające dla wszystkich 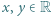 nierówność
nierówność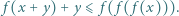
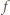 spełnia warunki zadania. Niech
spełnia warunki zadania. Niech 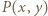 oznacza nierówność
oznacza nierówność 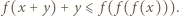 Wybierzmy dowolnie
Wybierzmy dowolnie 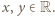 Ponieważ
Ponieważ 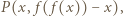 więc
więc 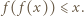 Podstawiając w ostatniej nierówności
Podstawiając w ostatniej nierówności 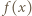 zamiast
zamiast  i uwzględniając
i uwzględniając 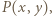 dostajemy
dostajemy 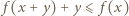 dla dowolnych
dla dowolnych 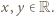 Podstawiając
Podstawiając 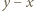 zamiast
zamiast 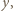 dostajemy
dostajemy 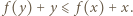 Z dowolności
Z dowolności 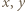 wnioskujemy, że
wnioskujemy, że 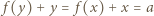 dla pewnego
dla pewnego 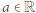 i wszystkich
i wszystkich 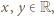 zatem musi być
zatem musi być 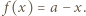 Łatwo sprawdzić, że ta funkcja faktycznie spełnia
Łatwo sprawdzić, że ta funkcja faktycznie spełnia 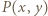 dla wszystkich
dla wszystkich 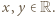
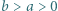 zachodzi nierówność
zachodzi nierówność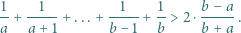
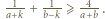
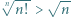 dla naturalnych
dla naturalnych 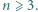
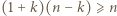 dla
dla 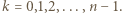 Ponadto dla
Ponadto dla 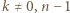 nierówność jest ostra.
nierówność jest ostra.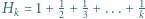 dla całkowitych dodatnich
dla całkowitych dodatnich 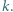 Udowodnić, że
Udowodnić, że 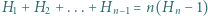 dla naturalnych
dla naturalnych 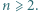
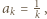 gdzie
gdzie 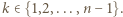
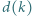 oznacza liczbę dzielników liczby naturalnej
oznacza liczbę dzielników liczby naturalnej 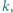 zaś
zaś 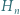 - jak w poprzednim zadaniu. Dowieść, że
- jak w poprzednim zadaniu. Dowieść, że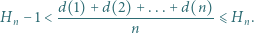
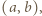 dla których
dla których 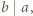 gdzie
gdzie 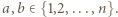 Po sporządzeniu tabeli w kolumnach mamy kolejno
Po sporządzeniu tabeli w kolumnach mamy kolejno 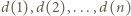 par, a w wierszach
par, a w wierszach 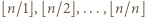 par. Trzeba jeszcze zastosować nierówność
par. Trzeba jeszcze zastosować nierówność 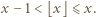
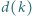 będzie jak w zadaniu 6. Ustalmy liczbę rzeczywistą
będzie jak w zadaniu 6. Ustalmy liczbę rzeczywistą 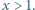 Dowieść, że dla wszystkich naturalnych
Dowieść, że dla wszystkich naturalnych 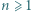 zachodzi nierówność
zachodzi nierówność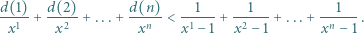
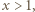 mamy
mamy 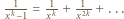 Dla
Dla 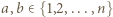 w polu
w polu 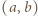 tabeli umieszczamy liczbę
tabeli umieszczamy liczbę 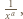 jeśli
jeśli 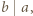 w przeciwnym razie umieszczamy 0. Sumując kolumnami, otrzymamy lewą stronę dowodzonej nierówności, natomiast wierszami - liczbę mniejszą od prawej strony.
w przeciwnym razie umieszczamy 0. Sumując kolumnami, otrzymamy lewą stronę dowodzonej nierówności, natomiast wierszami - liczbę mniejszą od prawej strony.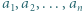 spełniają równości
spełniają równości 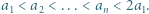 Udowodnić, że jeśli
Udowodnić, że jeśli 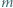 jest liczbą różnych dzielników pierwszych iloczynu
jest liczbą różnych dzielników pierwszych iloczynu 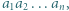 to
to 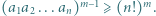
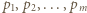 będą różnymi dzielnikami pierwszymi iloczynu
będą różnymi dzielnikami pierwszymi iloczynu 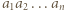 oraz niech
oraz niech 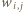 oznacza wykładnik liczby
oznacza wykładnik liczby 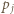 w rozkładzie
w rozkładzie 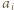 na czynniki pierwsze dla
na czynniki pierwsze dla 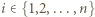 i
i 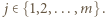 W pole tabeli o współrzędnych
W pole tabeli o współrzędnych 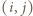 wpisujemy
wpisujemy 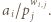 Należy zaobserwować, że w każdym wierszu są różne liczby całkowite dodatnie, więc ich iloczyn wynosi co najmniej
Należy zaobserwować, że w każdym wierszu są różne liczby całkowite dodatnie, więc ich iloczyn wynosi co najmniej 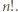 Ponadto iloczyny liczb w kolejnych kolumnach są równe
Ponadto iloczyny liczb w kolejnych kolumnach są równe 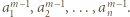
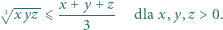
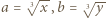 i
i 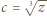 w tożsamości.
w tożsamości.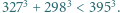 Uczynić to bez pomocy kalkulatora, wykonując przy tym możliwie najmniej rachunków.
Uczynić to bez pomocy kalkulatora, wykonując przy tym możliwie najmniej rachunków.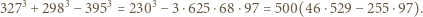
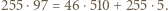
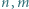 liczba rozwiązań nierówności
liczba rozwiązań nierówności 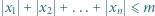 w liczbach całkowitych jest równa liczbie rozwiązań nierówności
w liczbach całkowitych jest równa liczbie rozwiązań nierówności 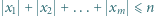 w liczbach całkowitych.
w liczbach całkowitych.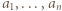 spełniają
spełniają 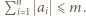 Możemy na dwa sposoby wskazać
Możemy na dwa sposoby wskazać 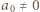 takie, że
takie, że 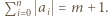 Każdy ciąg
Każdy ciąg 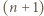 liczb spełniający tę równość (oraz
liczb spełniający tę równość (oraz 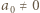 ) możemy podzielić na bloki, czyli fragmenty postaci
) możemy podzielić na bloki, czyli fragmenty postaci 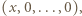 gdzie
gdzie 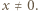 Jeśli długość takiego bloku to
Jeśli długość takiego bloku to 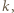 to przyporządkujemy mu blok
to przyporządkujemy mu blok 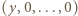 długości
długości 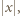 gdzie
gdzie 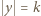 oraz
oraz 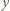 jest tego samego znaku, co
jest tego samego znaku, co 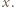 Wykonując tę operację na wszystkich blokach, dostaniemy ciąg
Wykonując tę operację na wszystkich blokach, dostaniemy ciąg 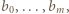 gdzie
gdzie 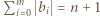 i
i 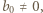 co daje nam ciąg liczb całkowitych
co daje nam ciąg liczb całkowitych 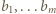 spełniający
spełniający 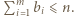 Nietrudno przekonać się, że przedstawione przekształcenie jest wzajemnie jednoznaczne, co kończy rozwiązanie.
Nietrudno przekonać się, że przedstawione przekształcenie jest wzajemnie jednoznaczne, co kończy rozwiązanie.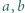 i
i  spełniają nierówność
spełniają nierówność 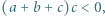 przy czym
przy czym 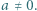 Wykazać, że
Wykazać, że 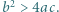
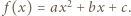 Wówczas mamy
Wówczas mamy 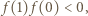 więc funkcja
więc funkcja 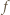 przyjmuje zarówno dodatnie i ujemne wartości, skąd
przyjmuje zarówno dodatnie i ujemne wartości, skąd 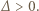


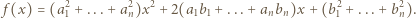
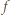 przyjmuje wyłącznie wartości nieujemne, więc
przyjmuje wyłącznie wartości nieujemne, więc 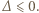 Jest to nierówność równoważna dowodzonej.
Jest to nierówność równoważna dowodzonej.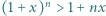 dla wszystkich liczb rzeczywistych
dla wszystkich liczb rzeczywistych 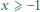 i liczb naturalnych
i liczb naturalnych 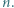
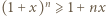 przez liczbę dodatnią
przez liczbę dodatnią 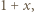 następnie wystarczy udowodnić, że
następnie wystarczy udowodnić, że