Fibonacci spotyka Banacha»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu Fibonacci spotyka Banacha
- Publikacja w Delcie: czerwiec 2020
- Publikacja elektroniczna: 31 maja 2020
Znaleźć liczbę wymierną  taką, że liczby
taką, że liczby 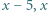 oraz
oraz 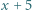 są kwadratami.
są kwadratami.
Znaleźć liczbę wymierną  taką, że liczby
taką, że liczby 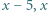 oraz
oraz 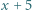 są kwadratami.
są kwadratami.
Niech 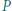 będzie wielomianem o współczynnikach wymiernych, który przyjmuje wartości niewymierne dla niewymiernych argumentów. Wykazać, że stopień
będzie wielomianem o współczynnikach wymiernych, który przyjmuje wartości niewymierne dla niewymiernych argumentów. Wykazać, że stopień 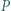 wynosi 1.
wynosi 1.
Dla każdej dodatniej liczby całkowitej 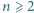 wyznaczyć taki wielomian
wyznaczyć taki wielomian 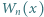 o współczynnikach wymiernych, że
o współczynnikach wymiernych, że
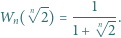
Wyznaczyć zbiór tych liczb wymiernych dodatnich, które można przedstawić w postaci ułamka  dla pewnych liczb naturalnych
dla pewnych liczb naturalnych 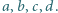
Zadanie 6 pochodzi z LXIV Olimpiady Matematycznej, a opisane tu rozwiązanie przedstawił jej uczestnik.
Czy istnieje wielomian o współczynnikach całkowitych, który nie jest różnowartościowy na zbiorze liczb rzeczywistych, ale jest różnowartościowy na zbiorze liczb wymiernych?
Znaleźć wszystkie liczby rzeczywiste niewymierne 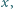 dla których każda z liczb
dla których każda z liczb 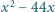 oraz
oraz 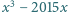 jest wymierna.
jest wymierna.
Rozstrzygnąć, czy istnieje taka dodatnia liczba wymierna 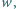 niebędąca liczbą całkowitą, że potęga
niebędąca liczbą całkowitą, że potęga 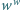 jest liczbą wymierną.
jest liczbą wymierną.
Zadanie 686 zaproponował pan Paweł Kubit z Krakowa
Udowodnić, że istnieje nieskończenie wiele liczb naturalnych 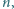 dla których równanie
dla których równanie 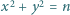 nie ma rozwiązań w liczbach całkowitych
nie ma rozwiązań w liczbach całkowitych 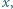
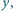 różnych od zera, ale ma rozwiązania w liczbach wymiernych
różnych od zera, ale ma rozwiązania w liczbach wymiernych 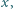
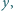 różnych od zera.
różnych od zera.
Dana jest liczba wymierna
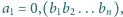 w której zapisie
dziesiętnym blok cyfr
w której zapisie
dziesiętnym blok cyfr
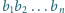 powtarza się okresowo po przecinku.
Rozważmy liczby
powtarza się okresowo po przecinku.
Rozważmy liczby
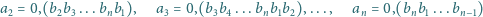
powstałe z
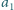 przez cykliczne przesunięcia cyfr w bloku. Udowodnić,
że
przez cykliczne przesunięcia cyfr w bloku. Udowodnić,
że
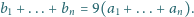
Rozstrzygnąć, czy istnieje taka dodatnia liczba wymierna
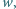 niebędąca
liczbą całkowitą, że potęga
niebędąca
liczbą całkowitą, że potęga
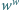 jest liczbą wymierną
jest liczbą wymierną
Wyznacz wszystkie takie liczby rzeczywiste
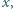 dla których liczby
dla których liczby
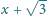 oraz
oraz
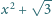 są wymierne.
są wymierne.
Zadanie 614 zaproponował pan Paweł Najman z Jaworzna.
Wyznaczyć wszystkie liczby wymierne
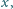 niecałkowite, dla których
wartość wyrażenia
niecałkowite, dla których
wartość wyrażenia
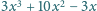 jest liczbą całkowitą.
jest liczbą całkowitą.
Dane są takie liczby wymierne
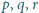 , dla których
, dla których
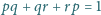 .
Wykazać, że liczba
.
Wykazać, że liczba
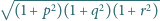
jest wymierna.