Czy każdy problem da się rozwiązać?
Czy każdy problem da się rozwiązać? Pesymiści odpowiedzą, że nie - życie nie jest łatwe. A optymiści? Być może niektórzy powiedzą, że przy odpowiednim podejściu tak. Nie będziemy jednak z nimi dyskutować, bo Czytelnicy Delty dobrze wiedzą, że nie chodzi nam tutaj przecież o życiowe problemy. Trzeba więc sprecyzować pytanie: co uważamy za problem i czym miałoby być jego rozwiązanie?

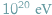 , co jest porównywalne ze zjawiskami makroskopowymi, np. energią jabłka spadającego z drzewa.
, co jest porównywalne ze zjawiskami makroskopowymi, np. energią jabłka spadającego z drzewa.
 ciał.
ciał.
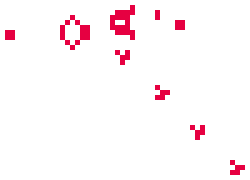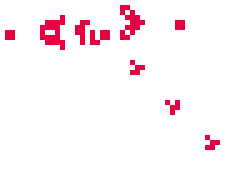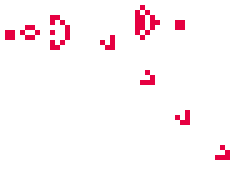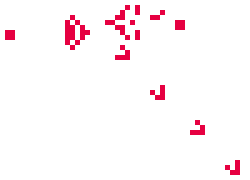
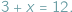 Gdy zamienimy występujące tu liczby miejscami, otrzymamy równanie
Gdy zamienimy występujące tu liczby miejscami, otrzymamy równanie 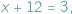 które "nie da się rozwiązać": gołym okiem widać, że wśród liczb, za pomocą których zwykliśmy liczyć krowy (czyli liczb naturalnych), nie znajdzie się żadna, która by spełniała to równanie...
które "nie da się rozwiązać": gołym okiem widać, że wśród liczb, za pomocą których zwykliśmy liczyć krowy (czyli liczb naturalnych), nie znajdzie się żadna, która by spełniała to równanie...