Budowle z klocków»Zadanie 4
o zadaniu...
- Zadanie pochodzi z artykułu Budowle z klocków
- Publikacja w Delcie: październik 2016
- Publikacja elektroniczna: 2 października 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (57 KB)
Udowodnij, że po usunięciu z kwadratu o krawędzi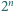 
dowolnego spośród 
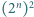tworzących go kwadratów jednostkowych powstaje figura, którą daje się szczelnie wypełnić klockami 
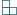, zbudowanymi z trzech kwadratów jednostkowych.
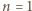teza jest prawdziwa: rozważana figura jest pojedynczym klockiem. Załóżmy, że teza zachodzi dla pewnego 
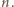Niech 
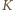będzie kwadratem o krawędzi 
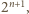z którego usuwamy jedno pole. Podzielmy 
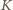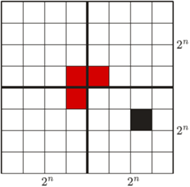
na cztery przystające mniejsze kwadraty o krawędzi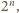 
jeden z nich zawiera usunięte pole. Umieśćmy pojedynczy klocek na środku kwadratu 
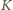w sposób przedstawiony na rysunku Wówczas na mocy założenia indukcyjnego każdy z czterech mniejszych kwadratów bez jednego pola da się szczelnie wypełnić klockami, co kończy dowód.