Proca grawitacyjna
Kiedy podrzucamy piłkę do góry, to przyciąganie grawitacyjne zawsze ją zawraca. Im mocniej ją podrzucimy -- czyli im większą nadamy jej energię -- tym wyżej poleci, zanim zawróci. Ale czy zawsze zawróci?
Kiedy podrzucamy piłkę do góry, to przyciąganie grawitacyjne zawsze ją zawraca. Im mocniej ją podrzucimy -- czyli im większą nadamy jej energię -- tym wyżej poleci, zanim zawróci. Ale czy zawsze zawróci?
Kiedy podrzucamy piłkę do góry, to przyciąganie grawitacyjne zawsze ją zawraca. Im mocniej ją podrzucimy -- czyli im większą nadamy jej energię -- tym wyżej poleci, zanim zawróci. Ale czy zawsze zawróci?
Gwiazdy, podobnie jak ludzi, można podzielić na pokolenia (populacje). Pierwsze historycznie obserwacje i podział na podgrupy przeprowadził Walter Baade, badając galaktykę M31 (Andromeda).

Astronomia Niebo jak własna kieszeń
Noc z 12 na 13 VII to najbardziej korzystny czas na obserwacje Merkurego. Tego dnia znajdzie się on w maksymalnej elongacji zachodniej od Słońca, czyli największej odległości kątowej na niebie od naszej dziennej gwiazdy. Merkury to najbliższa Słońcu planeta, która na niebie oddala się od Słońca najwyżej na 28 stopni.
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Materiały Aktualności (nie tylko) fizyczne
Etap rozwoju cywilizacyjnego można poznać po ilości i rodzaju śmieci, które dana cywilizacja po sobie zostawia. Obecny przełom tysiącleci to epoka tworzyw sztucznych. Ich dostępność i trwałość zmieniły nasze zwyczaje i zapewnią nam nieśmiertelność: [...] trza dzieciom ostawić długi. Wielgie długi, co by je spłacały. Bedóm długo spłocać, bedóm długo wiedzieć, ze miały ojca. (Józef Tischner, Historia filozofii po góralsku).
W okolicy mojego wydziału znajduje się stylowy bar mleczny. Potrawę należy wybrać przy kasie, zapłacić, a następnie podejść do „okienka”. Tam podajemy paragon i rozpoczynamy oczekiwanie na posiłek...
Od lat prowadzę ćwiczenia z przedmiotu Języki, Automaty i Obliczenia, w skrócie JAiO, zwanego potocznie „jajo”.
Algorytmy Informatyczny kącik olimpijski
W tym kąciku dwa zadania z cyklu naszych ulubionych, tzn. na pierwszy rzut oka ciężkie do ugryzienia, ale mające ładne i krótkie rozwiązania.
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
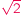 i jeszcze większe niemożliwości
i jeszcze większe niemożliwościPunktem wyjścia niech będzie najsłynniejsza chyba matematyczna konstatacja, ta
mianowicie, że liczba
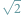 jest niewymierna...
jest niewymierna...

Wśród wielu typów zagadnień matematycznych bardzo sobie cenię takie, które po wierzchu są elementarne, łatwe na początku i dające się rozwiązać nietypowymi, efektownymi, niecodziennymi metodami. Dobrze jest też, gdy zadania te są wierzchołkiem pewnej góry lodowej, albo – stosując inne porównanie – są początkiem ścieżki wiodącej nas w nieznane.
Niektórzy sądzą, że geometria jest trudna. Oto zadanie, które wielu by odstraszyło...
Wiele wzorów na sumy kolejnych liczb naturalnych, ich kwadratów, sześcianów itp. można uzasadnić (lub przynajmniej przekonująco zilustrować) na rysunkach. Często rysunki te wymagają niewiele lub nawet zero komentarza – są to tzw. dowody bez słów...
W naszych rozważaniach wzbogacimy płaszczyznę o dodatkowy punkt, który
oznaczymy przez
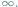 Przyjmiemy przy tym, że ów punkt leży na każdej
z prostych. Takie rozszerzone proste oraz okręgi obejmiemy wspólną nazwą
bloków...
Przyjmiemy przy tym, że ów punkt leży na każdej
z prostych. Takie rozszerzone proste oraz okręgi obejmiemy wspólną nazwą
bloków...
Starożytni Egipcjanie sprzed 4000 lat uznawali tylko ułamki proste, czyli takie, które w liczniku miały jedynkę. Oczywiście, były też inne ułamki, ale o nich uczeni mówić nie chcieli – przedstawiali je jako sumę ułamków prostych. Nie byłoby w tym niczego nadzwyczajnego, gdyby nie pretensjonalne wymaganie, aby w owej sumie każdy ułamek był inny.
Biologia Aktualności (nie tylko) fizyczne
Kultura matematyczna jest kluczowym aspektem ogólnoludzkiej kultury. Wykazano, że wiele gatunków zwierząt (badano głównie ssaki i ptaki) potrafi liczyć, tzn. prawidłowo oceniać liczebność zbiorów skończonych. Oczywiście, precyzja takiej oceny maleje wraz z tą liczebnością (np. przeciętni ludzie radzą sobie z takim liczeniem do około siedmiu).
Naukowcy uwielbiają unifikacje, czyli sytuacje, w których dwa na pozór różne zjawiska lub własności okazują się przejawami tego samego prawa lub przyczyny. Jedno z najbardziej znanych praw fizyki – prawo powszechnego ciążenia Newtona – jest w istocie pierwszym sukcesem programu unifikacji nowożytnej fizyki. Także i dzisiaj postulat unifikacji oddziaływań jest jedną z najważniejszych motywacji badań teoretycznych w fizyce cząstek elementarnych. Warto zatem przyjrzeć się bliżej, jak ta historia się zaczęła oraz jak się – przynajmniej na razie – kończy.

Rys. 1 Świat według Anaksymandra z Miletu.
Rys. 1 Świat według Anaksymandra z Miletu.
Starożytnym myślicielom zawdzięczamy przede wszystkim solidne naukowe podstawy uprawiania nauki. Opracowali oni założenia matematyki, logiki i geometrii, a w szczególności studiowali fizykę i filozofię z dociekliwością nie mniejszą niż współcześni badacze (a może o wiele większą, gdyż nie mieli do dyspozycji wyników doświadczeń Wielkiego Zderzacza Hadronów czy obserwacji teleskopu Hubble’a). Leukippos, Demokryt i Epikur wiedzieli na przykład, że materii nie da dzielić się w nieskończoność – składa się ona z niepodzielnych elementów (atomów), pomiędzy którymi znajduje się próżnia.

Maciej Geller (1941-2014)
Maciej Geller (1941-2014)
Historia i filozofia nauk Życie na żywo
Zorganizowana w maju przez Stowarzyszenie Otwarta Rzeczypospolita debata, prowadzona przez publicystkę Janinę Paradowską, z udziałem Moniki Płatek (prawniczka), Magdaleny Fikus (biolożka) i Zbigniewa Nosowskiego (publicysta), miała za myśl przewodnią zdanie wypowiedziane przez fizyka, wieloletniego dyrektora Festiwalu Nauki w Warszawie, Macieja Gellera (1941-2014): „Krytyk moich poglądów nie jest moim wrogiem, lecz współtowarzyszem w dążeniu do prawdy”...
