Zadanie ZM-14.07-inwersja-3
o zadaniu...
- Publikacja w Delcie: lipiec 2014
- Publikacja elektroniczna: 01-07-2014
Okręgi
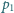 i
i
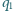 przecinają się w punktach
przecinają się w punktach
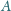 i
i
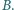 Prosta
Prosta
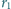 jest styczna do tych okręgów w punktach odpowiednio
jest styczna do tych okręgów w punktach odpowiednio
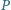 i
i
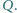 Punkt
Punkt
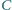 jest symetryczny do punktu
jest symetryczny do punktu
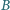 względem prostej
względem prostej
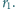 Okrąg
Okrąg
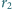 jest opisany na trójkącie
jest opisany na trójkącie
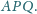 Proste
Proste
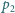 i
i
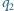 styczne do
styczne do
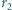 w punktach
odpowiednio
w punktach
odpowiednio
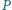 i
i
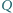 przecinają się w punkcie
przecinają się w punkcie
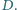 Wykazać,
że punkty
Wykazać,
że punkty
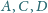 są współliniowe.
są współliniowe.

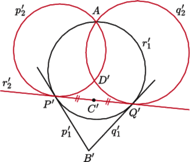
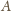 ; obraz każdej z figur oznaczmy przez dodanie znaku prim. Na
podstawie własności 1 możemy zauważyć, że figury z zadania
zamieniły się rolami: okręgi
; obraz każdej z figur oznaczmy przez dodanie znaku prim. Na
podstawie własności 1 możemy zauważyć, że figury z zadania
zamieniły się rolami: okręgi
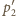 i
i
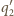 przecinają się w punktach
przecinają się w punktach
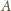 i
i
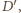 prosta
prosta
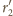 jest styczna do tych okręgów w punktach
jest styczna do tych okręgów w punktach
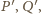 okrąg
okrąg
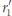 jest opisany na trójkącie
jest opisany na trójkącie
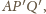 proste
proste
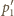 i
i
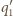 są styczne do
są styczne do
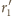 w punktach
w punktach
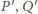 oraz
przecinają się w punkcie
oraz
przecinają się w punkcie
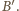
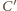 jest symetryczny do punktu
jest symetryczny do punktu
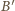 względem okręgu
względem okręgu
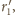 co na mocy zadania 1 oznacza, że jest
środkiem odcinka
co na mocy zadania 1 oznacza, że jest
środkiem odcinka
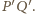 W ten sposób otrzymaliśmy konfigurację
z zadania 2, a zatem punkty
W ten sposób otrzymaliśmy konfigurację
z zadania 2, a zatem punkty
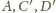 są współliniowe. Obrazem prostej
są współliniowe. Obrazem prostej
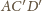 jest prosta
jest prosta
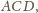 co kończy rozwiązanie.
co kończy rozwiązanie.