Co to jest?
Geometria różniczkowa
Geometria różniczkowa zajmuje się własnościami zbiorów opisanych przy użyciu funkcji różniczkowalnych (zwykle wielu zmiennych). Zbiory można opisywać m.in. przy użyciu układów równań lub za pomocą parametryzacji.

Rys. 1.
Na przykład układ równań

opisuje w trójwymiarowej przestrzeni 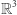 część wspólną sfery o promieniu 2 z walcem obrotowym o promieniu przekroju 1. Ta część wspólna jest linią o kształcie ósemki krzyżującej się ze sobą w punkcie, w którym walec jest styczny do sfery (Rys. 1). Zbadajmy, jak wygląda ta ósemka (jest to tzw. krzywa Vivianiego) w okolicy tego skrzyżowania. W tym celu opiszmy ją parametrycznie jako drogę przebytą przez punkt o współrzędnych
część wspólną sfery o promieniu 2 z walcem obrotowym o promieniu przekroju 1. Ta część wspólna jest linią o kształcie ósemki krzyżującej się ze sobą w punkcie, w którym walec jest styczny do sfery (Rys. 1). Zbadajmy, jak wygląda ta ósemka (jest to tzw. krzywa Vivianiego) w okolicy tego skrzyżowania. W tym celu opiszmy ją parametrycznie jako drogę przebytą przez punkt o współrzędnych

Dwa kolejne przejścia przez wierzchołek następują dla 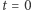 oraz dla
oraz dla 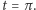 Rozpatrzmy wektor prędkości
Rozpatrzmy wektor prędkości
![p′(t) = [2cost,2 cos2t,−2 sin 2t]](/math/temat/matematyka/geometria/geometria_rozniczkowa/2019/03/28/Geometria_rozniczkowa/6x-b3b34adb52e4f03ad92ed0a240ec7dc23de0846d-dm-33,33,33-FF,FF,FF.gif)
poruszającego się punktu w chwili 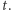 Ponieważ
Ponieważ ![|p′ (0) = [2,2,0]](/math/temat/matematyka/geometria/geometria_rozniczkowa/2019/03/28/Geometria_rozniczkowa/8x-b3b34adb52e4f03ad92ed0a240ec7dc23de0846d-im-33,33,33-FF,FF,FF.gif) i
i ![p′(π) = [− 2,2,0],](/math/temat/matematyka/geometria/geometria_rozniczkowa/2019/03/28/Geometria_rozniczkowa/9x-b3b34adb52e4f03ad92ed0a240ec7dc23de0846d-im-33,33,33-FF,FF,FF.gif) widzimy, że wędrujący po ósemce punkt przechodzi przez wierzchołek pod kątem
widzimy, że wędrujący po ósemce punkt przechodzi przez wierzchołek pod kątem  do osi walca, raz z jednej, raz z drugiej strony; zatem ósemka krzyżuje się ze sobą w wierzchołku pod kątem prostym. Czytelniku, spróbuj obliczyć kąt przecięcia w ósemce wyznaczonej przez walec o innym promieniu.
do osi walca, raz z jednej, raz z drugiej strony; zatem ósemka krzyżuje się ze sobą w wierzchołku pod kątem prostym. Czytelniku, spróbuj obliczyć kąt przecięcia w ósemce wyznaczonej przez walec o innym promieniu.

Rys. 2.
Pochodna parametryzacji 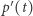 jest wektorem prędkości, druga pochodna
jest wektorem prędkości, druga pochodna 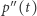 to wektor przyspieszenia. W sytuacji, gdy punkt porusza się wzdłuż krzywej z szybkością równą 1 (czyli długość wektora
to wektor przyspieszenia. W sytuacji, gdy punkt porusza się wzdłuż krzywej z szybkością równą 1 (czyli długość wektora 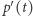 jest równa 1), punkt nie zwalnia i nie przyspiesza, więc jego wektor przyspieszenia
jest równa 1), punkt nie zwalnia i nie przyspiesza, więc jego wektor przyspieszenia 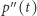 jest prostopadły do wektora prędkości i opisuje zmianę jego kierunku (Rys. 2). Długość wektora przyspieszenia nazywa się wtedy krzywizną danej krzywej w punkcie
jest prostopadły do wektora prędkości i opisuje zmianę jego kierunku (Rys. 2). Długość wektora przyspieszenia nazywa się wtedy krzywizną danej krzywej w punkcie 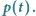 Im ta długość jest większa, tym ostrzej krzywa zakręca. Linia prosta ma w każdym punkcie zerową krzywiznę, a okrąg ma w każdym punkcie krzywiznę równą odwrotności promienia.
Im ta długość jest większa, tym ostrzej krzywa zakręca. Linia prosta ma w każdym punkcie zerową krzywiznę, a okrąg ma w każdym punkcie krzywiznę równą odwrotności promienia.
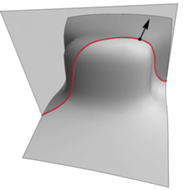
Rys. 3.
Rozpatrzmy teraz powierzchnię 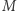 w przestrzeni trójwymiarowej
w przestrzeni trójwymiarowej  i punkt
i punkt  na niej oraz wybierzmy wektor
na niej oraz wybierzmy wektor 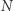 prostopadły do
prostopadły do 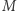 w punkcie
w punkcie  Dysponując pojęciem krzywizny krzywej, możemy zdefiniować krzywiznę powierzchni. Mianowicie, możemy rozpatrzyć wszystkie przekroje powierzchni
Dysponując pojęciem krzywizny krzywej, możemy zdefiniować krzywiznę powierzchni. Mianowicie, możemy rozpatrzyć wszystkie przekroje powierzchni 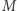 płaszczyznami zawierającymi punkt
płaszczyznami zawierającymi punkt 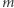 i wektor
i wektor 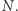 Dla każdego z tych przekrojów możemy obliczyć jego krzywiznę w punkcie
Dla każdego z tych przekrojów możemy obliczyć jego krzywiznę w punkcie 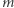 oraz przypisać jej znak plus, jeśli jej wektor przyspieszenia jest skierowany zgodnie z
oraz przypisać jej znak plus, jeśli jej wektor przyspieszenia jest skierowany zgodnie z  oraz znak minus w przeciwnym przypadku (Rys. 3). Okazuje się, że gdy będziemy obracać płaszczyznę przekroju wokół wektora
oraz znak minus w przeciwnym przypadku (Rys. 3). Okazuje się, że gdy będziemy obracać płaszczyznę przekroju wokół wektora 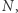 to krzywizna przekroju będzie się zmieniać między dwiema skrajnymi wartościami (noszą one nazwę krzywizn głównych). Iloczyn tych dwóch krzywizn nazywa się krzywizną Gaussa powierzchni w punkcie
to krzywizna przekroju będzie się zmieniać między dwiema skrajnymi wartościami (noszą one nazwę krzywizn głównych). Iloczyn tych dwóch krzywizn nazywa się krzywizną Gaussa powierzchni w punkcie 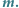 Na przykład krzywizna Gaussa walca w dowolnym punkcie jest równa 0, a krzywizna sfery o promieniu
Na przykład krzywizna Gaussa walca w dowolnym punkcie jest równa 0, a krzywizna sfery o promieniu  jest równa
jest równa  Krzywizna Gaussa ma ciekawą własność (udowodnioną przez Carla Gaussa): nie zmienia swojej wartości przy przekształceniu powierzchni zachowującym długości krzywych leżących na tej powierzchni. Oznacza to na przykład, że sfery (po rozcięciu) nie da się bez zmiany odległości przekształcić na kawałek płaszczyzny. Carl Gauss był tak dumny ze swojego twierdzenia, że nadał mu nazwę theorema egregium (twierdzenie chwalebne).
Krzywizna Gaussa ma ciekawą własność (udowodnioną przez Carla Gaussa): nie zmienia swojej wartości przy przekształceniu powierzchni zachowującym długości krzywych leżących na tej powierzchni. Oznacza to na przykład, że sfery (po rozcięciu) nie da się bez zmiany odległości przekształcić na kawałek płaszczyzny. Carl Gauss był tak dumny ze swojego twierdzenia, że nadał mu nazwę theorema egregium (twierdzenie chwalebne).

Rys. 4.
Do opisu krzywych wystarcza jeden parametr, do opisu powierzchni potrzeba dwóch parametrów. Na przykład położenie punktu na sferze o środku w punkcie 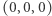 i promieniu
i promieniu  można opisać parametrycznie za pomocą dwóch parametrów (długości geograficznej
można opisać parametrycznie za pomocą dwóch parametrów (długości geograficznej 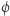 i szerokości geograficznej
i szerokości geograficznej 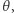 wzorem
wzorem 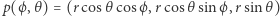 ), jednak żadnemu z biegunów
), jednak żadnemu z biegunów 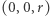 oraz
oraz 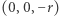 nie da się przypisać jednoznacznie pary współrzędnych. Można sparametryzować sferę bez jednego punktu za pomocą tzw. rzutu stereograficznego (w biegunie
nie da się przypisać jednoznacznie pary współrzędnych. Można sparametryzować sferę bez jednego punktu za pomocą tzw. rzutu stereograficznego (w biegunie 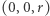 zapalamy żarówkę, a każdy punkt sfery rzuca cień na płaszczyznę styczną do sfery w przeciwnym biegunie
zapalamy żarówkę, a każdy punkt sfery rzuca cień na płaszczyznę styczną do sfery w przeciwnym biegunie 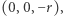 Rys. 4). Całej sfery jedną parametryzacją objąć się nie da.
Rys. 4). Całej sfery jedną parametryzacją objąć się nie da.
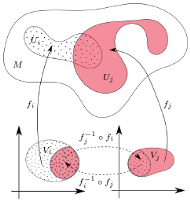
Rys. 5.
Uogólnieniem krzywych i powierzchni są rozmaitości różniczkowe dowolnego wymiaru, które lokalnie wyglądają jak przestrzeń 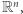 ale nie muszą być zawarte w żadnej konkretnej przestrzeni
ale nie muszą być zawarte w żadnej konkretnej przestrzeni 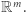 Rozmaitość różniczkowa wymiaru
Rozmaitość różniczkowa wymiaru  to zbiór pokryty podzbiorami
to zbiór pokryty podzbiorami 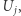 z których każdy posiada parametryzację
z których każdy posiada parametryzację 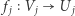 za pomocą funkcji różniczkowalnej
za pomocą funkcji różniczkowalnej  zmiennych określoną na otwartym podzbiorze
zmiennych określoną na otwartym podzbiorze 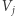 przestrzeni
przestrzeni 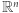 (Rys. 5).
(Rys. 5).
Przy tym parametryzacje nachodzących na siebie podzbiorów 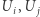 powinny być zgodne w tym sensie, że przekształcenie
powinny być zgodne w tym sensie, że przekształcenie  jest zadane funkcjami różniczkowalnymi. Na przykład dla sfery
jest zadane funkcjami różniczkowalnymi. Na przykład dla sfery  można jako kawałki
można jako kawałki 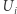 wybrać sześć półsfer opisanych nierównościami
wybrać sześć półsfer opisanych nierównościami

a jako ich parametryzacje przyjąć rzuty wzdłuż odpowiednich osi, np.

określić wzorem

Równie dobrze można użyć dwóch parametryzacji sferycznych lub dwóch rzutów stereograficznych. Takie podejście daje szersze możliwości. Na przykład za pomocą powyższej konstrukcji zastosowanej do trzech podzbiorów 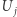 można opisać płaszczyznę rzutową, która nie jest powierzchnią orientowalną (zawiera wstęgę Möbiusa).
można opisać płaszczyznę rzutową, która nie jest powierzchnią orientowalną (zawiera wstęgę Möbiusa).