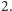Jak wygląda zbiór
 -wymiarowy, czyli
o wymiarze fraktali
-wymiarowy, czyli
o wymiarze fraktali

Pod koniec XIX wieku w matematyce zaczęły pojawiać się niespotykane wcześniej obiekty geometryczne, charakteryzujące się skomplikowanym kształtem i zjawiskiem „samopodobieństwa” (podobieństwa dowolnie małych fragmentów do całości zbioru). Tego rodzaju zbiory nazywamy dziś fraktalami. Aby lepiej opisać geometrię takich obiektów, wykorzystuje się różne odmiany pojęcia wymiaru, zwane czasami wymiarami fraktalnymi.
Co to znaczy, że linia prosta jest jednowymiarowa, płaszczyzna – dwuwymiarowa,
a przestrzeń, w której żyjemy – trójwymiarowa? Można na to pytanie
odpowiedzieć w ten sposób: na prostej możemy poruszać się w jednym
kierunku (właśnie wzdłuż tej prostej), na płaszczyźnie – w dwóch
niezależnych kierunkach, a w przestrzeni – w trzech (prawo-lewo,
przód-tył, góra-dół). (Pozostaje tylko sprecyzować, co to są niezależne
kierunki, co nie jest już takie oczywiste.) Mówiąc nieco inaczej, do
opisu punktu na prostej wystarczy jeden parametr rzeczywisty (jedna
współrzędna), punkty na płaszczyźnie mają dwie współrzędne itd.
Matematycy posługują się pojęciem przestrzeni
 -wymiarowej (dla
dowolnej liczby naturalnej
-wymiarowej (dla
dowolnej liczby naturalnej
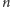 ), która jest zbiorem punktów opisanych
przez
), która jest zbiorem punktów opisanych
przez
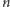 współrzędnych.
współrzędnych.
Sytuacja jest trudniejsza, gdy chcemy powiedzieć, jaki jest wymiar bardziej
skomplikowanych zbiorów. Naturalne jest przyjąć, że okrąg jest obiektem
jednowymiarowym, bo może być sparametryzowany jedną współrzędną
(kątem), a sfera (powierzchnia kuli) i torus (powierzchnia dętki) mają wymiar
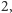 bo parametryzują się dwiema współrzędnymi kątowymi. Są to
przykłady tzw. gładkich rozmaitości, których wymiar jest łatwo określić
jako liczbę parametrów potrzebnych do ich opisania. Ogólniej, istnieje pojęcie
wymiaru topologicznego, który można zdefiniować dla szerokiej klasy
zbiorów (patrz artykuł na stronie 7 bieżącego numeru Delty). Taki wymiar
jest zawsze liczbą całkowitą.
bo parametryzują się dwiema współrzędnymi kątowymi. Są to
przykłady tzw. gładkich rozmaitości, których wymiar jest łatwo określić
jako liczbę parametrów potrzebnych do ich opisania. Ogólniej, istnieje pojęcie
wymiaru topologicznego, który można zdefiniować dla szerokiej klasy
zbiorów (patrz artykuł na stronie 7 bieżącego numeru Delty). Taki wymiar
jest zawsze liczbą całkowitą.
Pod koniec XIX wieku w matematyce zaczęły pojawiać się niespotykane wcześniej obiekty geometryczne, charakteryzujące się skomplikowanym kształtem i zjawiskiem „samopodobieństwa” (podobieństwa dowolnie małych fragmentów do całości zbioru). Tego rodzaju zbiory nazywamy dziś fraktalami. Aby lepiej opisać geometrię takich obiektów, wykorzystuje się różne odmiany pojęcia wymiaru, zwane czasami wymiarami fraktalnymi. W odróżnieniu od „zwykłego” wymiaru, mogą one przyjmować wartości niecałkowite. Przyjrzymy się teraz na kilku przykładach, jak można takie wymiary zdefiniować i jak je obliczać.
Jednym z pierwszych fraktali, który pojawił się w matematyce, była
krzywa Kocha, zwana też płatkiem śniegu (patrz rysunek). Przykład ten został
podany przez szwedzkiego matematyka Helge von Kocha w 1904 roku.
Jest to samopodobna krzywa zamknięta bez samoprzecięć, która ma
nieskończoną długość i nie ma stycznej w żadnym punkcie. Można
zauważyć, że chociaż krzywa Kocha jest topologicznie obiektem
jednowymiarowym, to zajmuje „więcej miejsca” na płaszczyźnie niż zwyczajna
gładka krzywa. Aby opisać liczbowo to zjawisko, można wprowadzić pojęcie
wymiaru samopodobieństwa (ang. similarity dimension). Zauważmy, że
jednowymiarowy odcinek ma następującą własność: dla każdej liczby
naturalnej
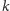 jest sumą
jest sumą
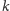 odcinków o długości
odcinków o długości
 razy
mniejszej, o rozłącznych wnętrzach (tzn. stykających się tylko końcami).
Każdy z tych odcinków jest obrazem dużego odcinka przy podobieństwie
o skali
razy
mniejszej, o rozłącznych wnętrzach (tzn. stykających się tylko końcami).
Każdy z tych odcinków jest obrazem dużego odcinka przy podobieństwie
o skali
 Mamy więc
Mamy więc

gdzie
 to skala podobieństwa, a
to skala podobieństwa, a
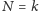 to liczba
przeskalowanych kopii dających w sumie cały zbiór. Spójrzmy teraz na
dwuwymiarowy kwadrat: jest on sumą
to liczba
przeskalowanych kopii dających w sumie cały zbiór. Spójrzmy teraz na
dwuwymiarowy kwadrat: jest on sumą
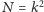 kwadratów o rozłącznych
wnętrzach (stykających się tylko brzegiem), które są obrazami dużego
kwadratu przy podobieństwach o skali
kwadratów o rozłącznych
wnętrzach (stykających się tylko brzegiem), które są obrazami dużego
kwadratu przy podobieństwach o skali
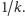 Mamy zatem
Mamy zatem

a więc wykładnik przy skali
 w powyższym wzorze to wymiar
obiektu (podobnie w poprzednim wzorze wykładnik przy
w powyższym wzorze to wymiar
obiektu (podobnie w poprzednim wzorze wykładnik przy
 równy
równy
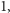 jest wymiarem odcinka). Dla trójwymiarowej kostki mamy,
analogicznie,
jest wymiarem odcinka). Dla trójwymiarowej kostki mamy,
analogicznie,

dla
 i
i
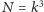 (kostka jest sumą
(kostka jest sumą
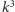 kostek o boku
kostek o boku
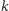 razy mniejszym, o rozłącznych wnętrzach) i znowu wykładnik przy
skali
razy mniejszym, o rozłącznych wnętrzach) i znowu wykładnik przy
skali
 jest równy wymiarowi zbioru. A jak jest dla krzywej Kocha?
Wygodnie jest podzielić ją na trzy części (każda powstała z jednego boku
dużego trójkąta) i rozpatrzyć każdą z nich osobno. Zauważmy,
że taka część jest sumą czterech swoich kopii (stykających się tylko
w pojedynczych punktach) przy odpowiednich podobieństwach o skali
jest równy wymiarowi zbioru. A jak jest dla krzywej Kocha?
Wygodnie jest podzielić ją na trzy części (każda powstała z jednego boku
dużego trójkąta) i rozpatrzyć każdą z nich osobno. Zauważmy,
że taka część jest sumą czterech swoich kopii (stykających się tylko
w pojedynczych punktach) przy odpowiednich podobieństwach o skali
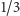 (patrz też strona 15). Wynika to wprost z konstrukcji płatka
śniegu. Jeśli więc wymiar takiej części byłby równy
(patrz też strona 15). Wynika to wprost z konstrukcji płatka
śniegu. Jeśli więc wymiar takiej części byłby równy
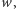 to
powinno zachodzić
to
powinno zachodzić

dla
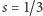 i
i
 czyli
czyli

To równanie jest spełnione dla
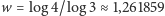 (zauważmy,
że można tu wziąć logarytm o dowolnej podstawie, co nie ma wpływu na
wynik). Tę właśnie liczbę
(zauważmy,
że można tu wziąć logarytm o dowolnej podstawie, co nie ma wpływu na
wynik). Tę właśnie liczbę
 nazywamy wymiarem samopodobieństwa
krzywej Kocha. Jest to liczba leżąca pomiędzy
nazywamy wymiarem samopodobieństwa
krzywej Kocha. Jest to liczba leżąca pomiędzy
 i
i
 co
odzwierciedla wysoki „stopień skomplikowania” tej krzywej.
co
odzwierciedla wysoki „stopień skomplikowania” tej krzywej.
Taki wymiar możemy łatwo obliczyć dla różnych samopodobnych zbiorów,
które są sumą kilku swoich kopii o rozłącznych „wnętrzach”, przy podobieństwach
o danej skali. Jeśli mamy
 takich kopii, a skala jest równa
takich kopii, a skala jest równa
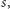 to
ten wymiar jest równy
to
ten wymiar jest równy
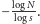 Na przykład, wymiar samopodobieństwa
trójkąta Sierpińskiego jest równy
Na przykład, wymiar samopodobieństwa
trójkąta Sierpińskiego jest równy
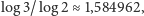 a dla zbioru
Cantora jest on równy
a dla zbioru
Cantora jest on równy
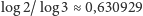 (patrz rysunki).
(patrz rysunki).
Możemy jeszcze uogólnić nasz wzór na przypadek, gdy badany obiekt jest
sumą
 swoich kopii o rozłącznych „wnętrzach”, uzyskanych przez
podobieństwa o różnych skalach, powiedzmy
swoich kopii o rozłącznych „wnętrzach”, uzyskanych przez
podobieństwa o różnych skalach, powiedzmy
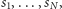 gdzie
gdzie
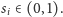 Wymiar samopodobieństwa jest wtedy taką liczbą
Wymiar samopodobieństwa jest wtedy taką liczbą
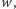 dla której zachodzi
dla której zachodzi

Taka liczba
 zawsze istnieje i jest wyznaczona jednoznacznie
(dlaczego?).
zawsze istnieje i jest wyznaczona jednoznacznie
(dlaczego?).
Wadą wymiaru samopodobieństwa jest to, że jest zdefiniowany tylko dla
szczególnego rodzaju zbiorów, uzyskanych przez procedury podobne do
opisanych powyżej. Dla innych zbiorów potrzebne jest więc ogólniejsze
pojęcie wymiaru „fraktalnego”. Zdefiniujemy teraz wymiar pudełkowy (ang. box
dimension, box-counting dimension), zwany też wymiarem Minkowskiego
lub Minkowskiego–Bouliganda. Oznaczany jest zwykle
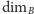 lub
lub
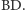
Weźmy pod uwagę dowolny ograniczony zbiór
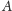 na płaszczyźnie. Dla
każdej liczby
na płaszczyźnie. Dla
każdej liczby
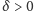 istnieje taka liczba naturalna
istnieje taka liczba naturalna
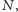 że możemy
pokryć nasz zbiór
że możemy
pokryć nasz zbiór
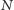 kwadratami o boku
kwadratami o boku
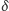 (dlaczego?). Niech
(dlaczego?). Niech
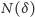 będzie najmniejszą taką liczbą
będzie najmniejszą taką liczbą
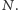 Wtedy wymiar pudełkowy
zbioru
Wtedy wymiar pudełkowy
zbioru
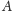 jest równy
jest równy

(podobnie jak poprzednio, ta wartość nie zależy od wyboru podstawy
logarytmu). Nietrudno wykazać (jak?), że wynik będzie ten sam, jeśli zamiast
dowolnych kwadratów o boku
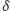 weźmiemy kwadraty tworzące
na płaszczyźnie kratę o boku
weźmiemy kwadraty tworzące
na płaszczyźnie kratę o boku
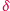 . Możemy też zastąpić kwadraty
kołami o średnicy
. Możemy też zastąpić kwadraty
kołami o średnicy

Jeśli zbiór jest podzbiorem prostej, to zamiast kwadratów bierzemy odcinki
o długości
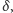 a jeśli jesteśmy w przestrzeni trójwymiarowej, to
kwadraty zastępujemy kostkami o boku
a jeśli jesteśmy w przestrzeni trójwymiarowej, to
kwadraty zastępujemy kostkami o boku
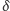 lub kulami o średnicy
lub kulami o średnicy
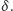 Ogólnie, definicję rozszerza się na ograniczone podzbiory przestrzeni
Ogólnie, definicję rozszerza się na ograniczone podzbiory przestrzeni
 -wymiarowej.
-wymiarowej.
Może się zdarzyć, że granica w definicji wymiaru pudełkowego nie istnieje. Wtedy trzeba zastąpić zwykłą granicę przez granicę górną lub dolną, uzyskując tzw. górny lub dolny wymiar pudełkowy.
Można łatwo sprawdzić (jak?), że wymiar pudełkowy odcinka jest równy
 kwadrat ma wymiar pudełkowy
kwadrat ma wymiar pudełkowy
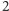 i tak dalej. A jaki jest
wymiar pudełkowy zbioru Cantora
i tak dalej. A jaki jest
wymiar pudełkowy zbioru Cantora
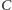 ? Dla
? Dla
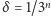 mamy
mamy
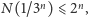 bo
bo
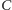 jest pokryty przez
jest pokryty przez
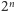 odcinków
o długości
odcinków
o długości
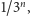 powstałych po
powstałych po
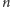 krokach konstrukcji. Z drugiej
strony, końce tych wszystkich odcinków należą do zbioru Cantora, a „dziury”
między nimi są długości co najmniej
krokach konstrukcji. Z drugiej
strony, końce tych wszystkich odcinków należą do zbioru Cantora, a „dziury”
między nimi są długości co najmniej
 i łatwo zauważyć, że
i łatwo zauważyć, że
 Mamy więc
Mamy więc
 więc
więc

co jest równe wymiarowi samopodobieństwa. Pozostawiamy Czytelnikowi
sprawdzenie, że przy obliczaniu granicy w definicji wymiaru pudełkowego
wystarczy brać
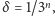 co daje
co daje

Podobnie wyznaczamy wymiar pudełkowy trójkąta Sierpińskiego i krzywej Kocha. We wszystkich tych przykładach (i podobnych konstrukcjach) wymiar pudełkowy jest równy wymiarowi samopodobieństwa.
Wymiar pudełkowy nie ma jednak najlepszych własności matematycznych.
Na przykład, okazuje się, że wymiar pudełkowy domknięcia zbioru
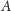 jest taki sam, jak wymiar samego zbioru
jest taki sam, jak wymiar samego zbioru
 co implikuje
w szczególności, że zbiór liczb wymiernych w odcinku
co implikuje
w szczególności, że zbiór liczb wymiernych w odcinku
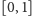 ma
wymiar pudełkowy
ma
wymiar pudełkowy
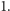 Przy „porządnej” definicji wymiaru każdy
przeliczalny zbiór powinien mieć wymiar zero! Jakie jest więc pojęcie
fraktalnego wymiaru, które zadowoli wymagającego matematyka?
Przy „porządnej” definicji wymiaru każdy
przeliczalny zbiór powinien mieć wymiar zero! Jakie jest więc pojęcie
fraktalnego wymiaru, które zadowoli wymagającego matematyka?
Takim wymiarem jest wymiar Hausdorffa, zwany też czasami wymiarem Hausdorffa–Besicovitcha. Jego definicja jest jednak znacznie bardziej skomplikowana niż poprzednie. Omówimy ją teraz.
Niech
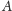 będzie dowolnym podzbiorem
będzie dowolnym podzbiorem
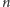 -wymiarowej przestrzeni
-wymiarowej przestrzeni
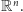 Ustalmy
Ustalmy
 Weźmy pod uwagę dowolne przeliczalne
pokrycie zbioru
Weźmy pod uwagę dowolne przeliczalne
pokrycie zbioru
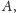 to znaczy zbiory
to znaczy zbiory
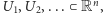 takie
że
takie
że
 (Zamiast dowolnych zbiorów można wziąć
kule w
(Zamiast dowolnych zbiorów można wziąć
kule w
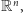 to znaczy odcinki na prostej dla
to znaczy odcinki na prostej dla
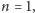 koła na
płaszczyźnie dla
koła na
płaszczyźnie dla
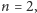 zwykłe kule w przestrzeni trójwymiarowej dla
zwykłe kule w przestrzeni trójwymiarowej dla
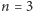 itd.) Dla danej liczby
itd.) Dla danej liczby
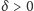

gdzie
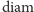 oznacza średnicę zbioru, a infimum jest wzięte po wszystkich
takich pokryciach
oznacza średnicę zbioru, a infimum jest wzięte po wszystkich
takich pokryciach
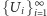 zbioru
zbioru
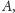 że
że
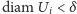 dla
wszystkich
dla
wszystkich
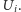 Bierzemy teraz
Bierzemy teraz

Ta granica zawsze istnieje (być może równa
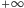 ), bo
), bo
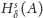 maleje
przy wzroście
maleje
przy wzroście
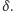 Liczbę
Liczbę
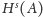 nazywamy
nazywamy
 -tą miarą (
zewnętrzną) Hausdorffa zbioru
-tą miarą (
zewnętrzną) Hausdorffa zbioru
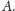 Okazuje się, że istnieje taka
liczba
Okazuje się, że istnieje taka
liczba
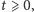 że
że
 dla wszystkich
dla wszystkich
 i
i
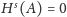 dla wszystkich
dla wszystkich
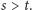 Tę liczbę
Tę liczbę
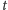 nazywamy
wymiarem Hausdorffa zbioru
nazywamy
wymiarem Hausdorffa zbioru
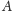 i oznaczamy
i oznaczamy
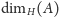 lub
lub
 Dla
Dla
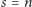 miara Hausdorffa jest równoważna „zwykłej”
mierze Lebesgue’a w
miara Hausdorffa jest równoważna „zwykłej”
mierze Lebesgue’a w
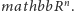
Wymiar Hausdorffa ma dobre właściwości matematyczne. Można
sprawdzić, że
 i
i
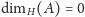 dla każdego
przeliczalnego zbioru
dla każdego
przeliczalnego zbioru
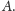 Poza tym,
Poza tym,
 dla
każdej gładkiej rozmaitości
dla
każdej gładkiej rozmaitości
 -wymiarowej
-wymiarowej
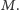 Mamy
też
Mamy
też
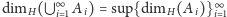 dla dowolnych zbiorów
dla dowolnych zbiorów
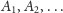 Wadą wymiaru Hausdorffa jest to, że zazwyczaj jest trudny do
obliczenia! Już obliczenie tego wymiaru dla zbioru Cantora nastręcza
trudności, a przypadek trójkąta Sierpińskiego czy krzywej Kocha
wymaga zastosowania odpowiednich narzędzi z geometrycznej teorii miary,
teorii potencjału lub transformaty Fouriera. Pewnym ułatwieniem jest
nierówność
Wadą wymiaru Hausdorffa jest to, że zazwyczaj jest trudny do
obliczenia! Już obliczenie tego wymiaru dla zbioru Cantora nastręcza
trudności, a przypadek trójkąta Sierpińskiego czy krzywej Kocha
wymaga zastosowania odpowiednich narzędzi z geometrycznej teorii miary,
teorii potencjału lub transformaty Fouriera. Pewnym ułatwieniem jest
nierówność

która zachodzi dla wszystkich zbiorów
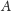 (jeśli granica w definicji
wymiaru pudełkowego nie istnieje, to bierzemy dolny wymiar pudełkowy).
W przypadku zbioru Cantora, krzywej Kocha i trójkąta Sierpińskiego mamy
równość wymiarów Hausdorffa i pudełkowego, jednak taka sytuacja
nie zawsze zachodzi.
(jeśli granica w definicji
wymiaru pudełkowego nie istnieje, to bierzemy dolny wymiar pudełkowy).
W przypadku zbioru Cantora, krzywej Kocha i trójkąta Sierpińskiego mamy
równość wymiarów Hausdorffa i pudełkowego, jednak taka sytuacja
nie zawsze zachodzi.

Wolfgang Beyer / wikipedia
W 1991 roku Mitsuhiro Shishikura udowodnił, że brzeg zbioru Mandelbrota ma wymiar
Hausdorffa równy
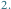
Zadanie. Niech
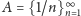 i
i
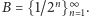 Udowodnić, że
Udowodnić, że

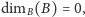
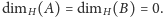
Odnotujmy jeszcze ważne twierdzenie Szpilrajna, mówiące o tym, że wymiar Hausdorffa jest większy lub równy wymiarowi topologicznemu. Z tego powodu fraktale można zdefiniować jako zbiory, dla których ta nierówność jest ostra.
Jest jeszcze kilka innych wymiarów fraktalnych, takich jak wymiar Rényi, wymiar korelacyjny czy wymiar pakujący, ale nie będziemy tu o nich mówili.
Na koniec odpowiemy na pytanie zawarte w tytule: jak może wyglądać zbiór
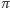 -wymiarowy? Aby zdefiniować taki zbiór, przeprowadzimy konstrukcję
podobną jak dla zbioru Cantora, z tym że w każdym kroku będziemy zmieniać
liczbę wyjętych odcinków i skalę zmniejszania. Niech dla każdej liczby naturalnej
-wymiarowy? Aby zdefiniować taki zbiór, przeprowadzimy konstrukcję
podobną jak dla zbioru Cantora, z tym że w każdym kroku będziemy zmieniać
liczbę wyjętych odcinków i skalę zmniejszania. Niech dla każdej liczby naturalnej
 zbiór
zbiór
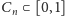 składa się z
składa się z
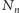 rozłącznych odcinków
o długości
rozłącznych odcinków
o długości
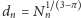 każdy, rozłożonych tak, że odległości
między środkami kolejnych odcinków są równe
każdy, rozłożonych tak, że odległości
między środkami kolejnych odcinków są równe
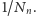 Definiujemy
zbiór „typu Cantora” jako
Definiujemy
zbiór „typu Cantora” jako
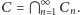 Okazuje się, że jeżeli liczby
Okazuje się, że jeżeli liczby
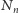 rosną dostatecznie szybko wraz ze wzrostem
rosną dostatecznie szybko wraz ze wzrostem
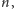 to wymiar
Hausdorffa zbioru
to wymiar
Hausdorffa zbioru
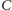 jest równy
jest równy
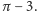 Nie dowodzimy tutaj tego,
zauważmy tylko, że
Nie dowodzimy tutaj tego,
zauważmy tylko, że

Wtedy zbiór
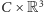 (iloczyn kartezjański zbioru
(iloczyn kartezjański zbioru
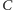 i przestrzeni
trójwymiarowej), zawarty w przestrzeni czterowymiarowej, ma wymiar Hausdorffa
równy
i przestrzeni
trójwymiarowej), zawarty w przestrzeni czterowymiarowej, ma wymiar Hausdorffa
równy
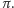
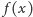 przy
przy
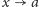 to największa
(najmniejsza) z granic ciągu
to największa
(najmniejsza) z granic ciągu
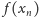 przy dowolnym wyborze ciągu
przy dowolnym wyborze ciągu
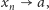
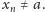
 km do
km do
 m). Okazało się, że jest on większy od
m). Okazało się, że jest on większy od
 i wynosi około
i wynosi około
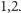
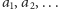 Takim zbiorem jest np. zbiór liczb
wymiernych.
Takim zbiorem jest np. zbiór liczb
wymiernych.