Algorytmy Informatyczny kącik olimpijski
Dwa torty
W tym kąciku omówimy Dwa torty – kolejne zadanie z finałowej rundy Potyczek Algorytmicznych 2012.
Algorytmy Informatyczny kącik olimpijski
W tym kąciku omówimy Dwa torty – kolejne zadanie z finałowej rundy Potyczek Algorytmicznych 2012.
Jedną z najczęściej wykonywanych operacji w geometrii obliczeniowej jest sortowanie
biegunowe (zwane też kątowym) zbioru
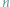 punktów na płaszczyźnie
względem wybranego punktu. Innymi słowy, chcemy uporządkować punkty
punktów na płaszczyźnie
względem wybranego punktu. Innymi słowy, chcemy uporządkować punkty
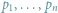 według współrzędnej kątowej w układzie biegunowym zaczepionym
w wybranym punkcie
według współrzędnej kątowej w układzie biegunowym zaczepionym
w wybranym punkcie
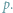 Stosując jeden z efektywnych algorytmów sortowania,
operację tę można zrealizować w czasie
Stosując jeden z efektywnych algorytmów sortowania,
operację tę można zrealizować w czasie
Czy programy liniowe mają coś wspólnego z informatyką? Okazuje się, że bardzo wiele. Po pierwsze, istnieją (bardzo ciekawe!) efektywne algorytmy rozwiązujące programy liniowe. Ponadto, programy liniowe są kluczowym narzędziem w optymalizacji kombinatorycznej, algorytmach aproksymacyjnych czy algorytmach online...
„Tato, jak policzyć do nieskończoności?” – takie pytanie zadał mi niedawno mój czteroletni syn. Odpowiedziałem coś w stylu „nigdy nie skończysz”. W każdym razie liczenie do nieskończoności może się relatywnie szybko znudzić, może więc to zadanie, jak wiele innych monotonnych zadań, powierzyć komputerowi? A czy komputer potrafi policzyć do nieskończoności?
Algorytmy Informatyczny kącik olimpijski
Jednym z klasycznych problemów algorytmicznych jest tzw. problem plecakowy...

W dniach 12-15 marca 2013 r. w Warszawie odbyły się zawody III stopnia jubileuszowej, XX Olimpiady Informatycznej. Do finału zostało zakwalifikowanych 96 zawodników. W ciągu dwóch dni zawodów finałowych zawodnicy mieli do rozwiązania w sumie sześć zadań programistycznych ocenianych od 0 do 100 punktów.
ASCII. Podstawowym sposobem reprezentacji znaków we współczesnych komputerach jest przyjęty w 1967 r. ASCII (czyt. aski, ang. American Standard Code for Information Interchange). Definiuje on 128 znaków, wśród których znajdują się 33 niedrukowalne znaki sterujące, znak odstępu, 52 litery (wielkie i małe litery alfabetu angielskiego), 10 cyfr i 32 znaki interpunkcyjne. ASCII przyporządkowuje każdemu znakowi liczbę z zakresu 0–127 (lub równoważnie szesnastkowo 0–7F).
Kiedy rozwiązujemy jakiś problem informatyczny, często naszym celem jest podanie jak
najefektywniejszego algorytmu. Jednak czasem możemy natknąć się przy
tym na „ścianę” – danego problemu nie da się rozwiązać tak efektywnie, jak
byśmy tego chcieli. Najpowszechniej znanym przykładem opisanego zjawiska jest
klasa problemów NP-zupełnych. O problemach z tej klasy (a należy do niej
wiele naturalnych i praktycznych zagadnień) podejrzewa się, że nie da się ich
rozwiązać w czasie wielomianowym względem rozmiaru danych wejściowych.
Niestety, tylko podejrzewa się, a rozstrzygnięcie tej hipotezy (znanej też jako
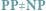 ?) jest obecnie najsłynniejszym otwartym problemem informatyki
teoretycznej.
?) jest obecnie najsłynniejszym otwartym problemem informatyki
teoretycznej.
Algorytmy Informatyczny kącik olimpijski
Tym razem zajmiemy się zadaniem z finałów Akademickich Mistrzostw Świata w Programowaniu Zespołowym 2012, które odbyły się w Warszawie. Zadanie zatytułowane Infiltration zostało rozwiązane przez 31 spośród 112 drużyn i było średnim pod względem trudności zadaniem na tych zawodach.
Na artykule Problemy 3sum-trudne w geometrii autor podał trzy wersje problemu PolygonContainment, które są uważane za trudne – nie umiemy ich rozwiązać w czasie (istotnie) lepszym niż kwadratowy. Uważni Czytelnicy na pewno zauważyli, że nie jest tam wspomniane o wersji, w której wielokąty są wypukłe i dopuszczamy dowolne przesunięcia (ale nie obroty). Ten brak jest w pełni uzasadniony, gdyż tę wersję problemu można rozwiązać w czasie liniowym względem liczby wierzchołków wielokątów, co pokażemy poniżej.
O zadaniu z Akademickich Mistrzostw Polski w Programowaniu Zespołowym (2012)
Algorytmy Informatyczny kącik olimpijski
W tym kąciku zajmiemy się zadaniem Quadrilaterals z obozu w Petrozawodsku
w 2006 roku. Na płaszczyźnie dane jest
 punktów w położeniu ogólnym
(tzn. żadna trójka punktów nie leży na jednej prostej). Należy wyznaczyć liczbę
czworokątów wypukłych, których wierzchołki znajdują się wśród podanych
punktów.
punktów w położeniu ogólnym
(tzn. żadna trójka punktów nie leży na jednej prostej). Należy wyznaczyć liczbę
czworokątów wypukłych, których wierzchołki znajdują się wśród podanych
punktów.
Dany jest graf nieskierowany
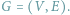 Kliką nazwiemy taki podzbiór
wierzchołków
Kliką nazwiemy taki podzbiór
wierzchołków
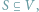 że każde dwa wierzchołki w zbiorze
że każde dwa wierzchołki w zbiorze
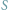 są
połączone krawędzią w grafie
są
połączone krawędzią w grafie
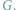 Problem znalezienia w grafie kliki o jak
największej liczbie wierzchołków jest NP-zupełny, a jak wiadomo, dla takich
problemów nikt jeszcze nie pokazał algorytmu wielomianowego. Podobne trudności są
z algorytmem dla problemu zliczania klik w grafie, choć tutaj stosowną klasę
złożoności stanowią tzw. problemy #P-zupełne.
Problem znalezienia w grafie kliki o jak
największej liczbie wierzchołków jest NP-zupełny, a jak wiadomo, dla takich
problemów nikt jeszcze nie pokazał algorytmu wielomianowego. Podobne trudności są
z algorytmem dla problemu zliczania klik w grafie, choć tutaj stosowną klasę
złożoności stanowią tzw. problemy #P-zupełne.
Algorytmy Informatyczny kącik olimpijski
Zadanie Odśnieżanie z zeszłorocznego Obozu Naukowo-Treningowego im. A. Kreczmara
można sformułować w języku teorii grafów następująco. W nieskierowanym,
ważonym, spójnym grafie
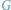 wyróżniono cztery wierzchołki. Należy
usunąć część krawędzi z grafu tak, żeby nadal istniały ścieżki pomiędzy każdą
parą wyróżnionych wierzchołków i żeby suma wag krawędzi, które pozostały
w grafie, była jak najmniejsza.
wyróżniono cztery wierzchołki. Należy
usunąć część krawędzi z grafu tak, żeby nadal istniały ścieżki pomiędzy każdą
parą wyróżnionych wierzchołków i żeby suma wag krawędzi, które pozostały
w grafie, była jak najmniejsza.
Podziały liczb są ciekawymi obiektami kombinatorycznymi o dosyć skomplikowanych
własnościach. W tym artykule przedstawimy dwa algorytmy zliczania takich
obiektów. Pierwszy prosty algorytm będzie działał w czasie
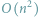 i pamięci
i pamięci
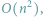 natomiast drugi, pochodzący od Eulera i oparty na tzw. liczbach
pentagonalnych, w czasie
natomiast drugi, pochodzący od Eulera i oparty na tzw. liczbach
pentagonalnych, w czasie
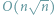 i pamięci
i pamięci
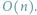
Algorytmy Informatyczny kącik olimpijski
W niedawno wydanej książce W poszukiwaniu wyzwań – zbiorze zadań
z konkursów programistycznych – Filip Wolski opisał rozwiązanie zadania Dwa
przyjęcia z finału XII Olimpiady Informatycznej. W zadaniu tym występuje
 osób, z których niektóre się znają (wiemy które). Chcemy podzielić ten
zbiór na dwa rozłączne podzbiory (przyjęcia) w taki sposób, aby zmaksymalizować
liczbę osób, które mają parzystą liczbę znajomych na przyjęciu, na którym
przebywają...
osób, z których niektóre się znają (wiemy które). Chcemy podzielić ten
zbiór na dwa rozłączne podzbiory (przyjęcia) w taki sposób, aby zmaksymalizować
liczbę osób, które mają parzystą liczbę znajomych na przyjęciu, na którym
przebywają...
Podobnie jak wyznaczanie liczb pierwszych, problem znajdowania największego
wspólnego dzielnika (NWD) dwóch liczb naturalnych ma klasyczne i zapewne
wszystkim Czytelnikom znane rozwiązanie. Mowa oczywiście o algorytmie
Euklidesa, jednym z najstarszych do dziś używanych algorytmów. Jest to
rozwiązanie bardzo proste w implementacji, a w wersji z dzieleniem – efektywne:
pozwala wyznaczyć NWD dwóch liczb nie większych niż
 w czasie
w czasie
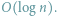 W pewnych przypadkach istnieją jednak rozwiązania asymptotycznie
szybsze.
W pewnych przypadkach istnieją jednak rozwiązania asymptotycznie
szybsze.
Jeśli potrzebne nam są do czegoś liczby pierwsze z pewnego początkowego zakresu, zazwyczaj wyznaczamy je za pomocą sita Eratostenesa...

Zapewne zdecydowana większość Czytelników ma skrzynkę poczty elektronicznej. Dostęp do skrzynki uzyskuje się przez podanie w specjalnym formularzu na stronie internetowej nazwy użytkownika i hasła. Te dane są następnie szyfrowane i wysyłane do serwera pocztowego, który porównuje je z umieszczonymi na nim wzorcami. Tak, w dużym uproszczeniu, wygląda proces weryfikacji użytkownika na serwerze.
Algorytmy Informatyczny kącik olimpijski
W tej edycji kącika omówimy zadanie pt. Podlewanie ogórków (naprawdę!) z rundy 2A konkursu TopCoder Open 2012.

Drodzy Czytelnicy Delty, przedstawiamy Wam zadania zawodów I stopnia jubileuszowej, XX Olimpiady Informatycznej. Tych z Was, którzy chcą wziąć udział w Olimpiadzie, zobowiązujemy do przeczytania „Zasad organizacji zawodów XX OI”, w których zawarte są najważniejsze informacje o tym, w jaki sposób należy przygotować swoje rozwiązania. Rozwiązania należy zgłaszać przez stronę sio.mimuw.edu.pl, na której znajdują się także wybrane odpowiedzi na pytania zawodników, narzędzia do sprawdzania rozwiązań pod względem formalnym oraz forum służące do wymiany doświadczeń między zawodnikami. Termin nadsyłania rozwiązań przedstawionych tu zadań I etapu upływa 12 listopada 2012 roku.
Algorytmy Informatyczny kącik olimpijski
Tym razem omówimy zadanie z pogranicza informatyki i muzykologii, które pojawiło się na Bałtyckiej Olimpiadzie Informatycznej w bieżącym roku.
Jak czarne dziury, odległe supernowe i inne wydarzenia kosmiczne mogą wpłynąć na bezpieczeństwo systemów komputerowych?
Algorytmy Informatyczny kącik olimpijski
Tym razem w kąciku lekko zmodyfikowana wersja zadania Listonosz z konkursu Wielka Przesmycka 2004.