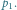Sortowanie biegunowe a dualizacja
Jedną z najczęściej wykonywanych operacji w geometrii obliczeniowej jest
sortowanie biegunowe (zwane też kątowym) zbioru
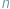 punktów
na płaszczyźnie względem wybranego punktu. Innymi słowy, chcemy
uporządkować punkty
punktów
na płaszczyźnie względem wybranego punktu. Innymi słowy, chcemy
uporządkować punkty
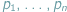 według współrzędnej kątowej
w układzie biegunowym zaczepionym w wybranym punkcie
według współrzędnej kątowej
w układzie biegunowym zaczepionym w wybranym punkcie
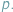 Stosując
jeden z efektywnych algorytmów sortowania, operację tę można zrealizować
w czasie
Stosując
jeden z efektywnych algorytmów sortowania, operację tę można zrealizować
w czasie
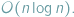
W wielu zastosowaniach musimy jednak pójść o krok dalej i wyznaczyć
uporządkowanie biegunowe punktów
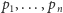 najpierw w układzie
biegunowym zaczepionym w
najpierw w układzie
biegunowym zaczepionym w
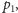 potem zaczepionym w
potem zaczepionym w
 itd.
Mamy zatem do wykonania
itd.
Mamy zatem do wykonania
 sortowań, co łącznie możemy
zrealizować w czasie
sortowań, co łącznie możemy
zrealizować w czasie
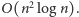 Okazuje się jednak, że istnieje
algorytm pozwalający wyznaczyć wszystkie potrzebne porządki biegunowe
w czasie
Okazuje się jednak, że istnieje
algorytm pozwalający wyznaczyć wszystkie potrzebne porządki biegunowe
w czasie
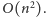 Jest on ciekawy, jednak dosyć trudny – w tym artykule
przedstawimy szkic tego algorytmu.
Jest on ciekawy, jednak dosyć trudny – w tym artykule
przedstawimy szkic tego algorytmu.
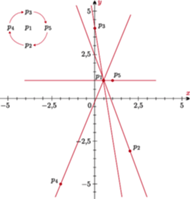
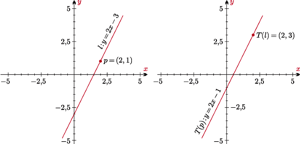
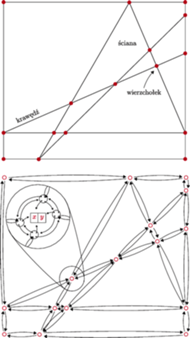
Rys. 1 Proste z
 oraz porządek biegunowy punktów względem
oraz porządek biegunowy punktów względem
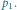
Punkty i proste
Pomyślmy o zbiorze punktów
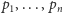 na płaszczyźnie. Wybierzmy
jeden z nich, na przykład
na płaszczyźnie. Wybierzmy
jeden z nich, na przykład
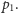 Poprowadźmy proste przez
Poprowadźmy proste przez
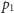 tak,
by połączyć go ze wszystkimi pozostałymi punktami
tak,
by połączyć go ze wszystkimi pozostałymi punktami
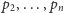 (Rys. 1). Każdemu z tych punktów odpowiada jedna prosta. Gdybyśmy
umieli posortować te proste według kąta nachylenia lub, inaczej mówiąc,
według współczynnika kierunkowego
(Rys. 1). Każdemu z tych punktów odpowiada jedna prosta. Gdybyśmy
umieli posortować te proste według kąta nachylenia lub, inaczej mówiąc,
według współczynnika kierunkowego
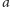 w równaniu prostej
w równaniu prostej
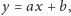 to takie uporządkowanie pozwoliłoby nam uzyskać
kolejność biegunową punktów
to takie uporządkowanie pozwoliłoby nam uzyskać
kolejność biegunową punktów
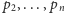 w układzie o środku
w
w układzie o środku
w
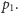
Spójrzmy teraz na wszystkie proste przechodzące przez pary punktów ze zbioru
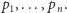 Jest ich nie więcej niż
Jest ich nie więcej niż
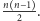 Jeśli uda nam się
skonstruować algorytm, który dla każdego z punktów posortuje
Jeśli uda nam się
skonstruować algorytm, który dla każdego z punktów posortuje
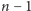 przechodzących przez niego prostych w sumarycznym czasie
lepszym niż
przechodzących przez niego prostych w sumarycznym czasie
lepszym niż
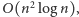 to dostaniemy lepsze rozwiązanie całego
zadania. Algorytm nie może jednak działać szybciej niż
to dostaniemy lepsze rozwiązanie całego
zadania. Algorytm nie może jednak działać szybciej niż
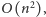 bo
taka jest liczba prostych, które ma posortować. Okazuje się, że algorytm
działający w czasie kwadratowym istnieje i opiera się na bardzo ciekawej
konstrukcji myślowej zwanej dualizacją.
bo
taka jest liczba prostych, które ma posortować. Okazuje się, że algorytm
działający w czasie kwadratowym istnieje i opiera się na bardzo ciekawej
konstrukcji myślowej zwanej dualizacją.
Dualizacja
Wyobraźmy sobie przekształcenie geometryczne
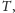 które punktowi
które punktowi
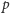 przyporządkowuje prostą
przyporządkowuje prostą
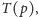 a prostej
a prostej
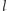 punkt
punkt
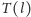 w następujący sposób:
w następujący sposób:
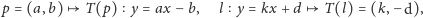 |
czyli punktowi o współrzędnych
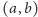 odpowiada prosta o równaniu
odpowiada prosta o równaniu
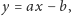 a prostej o równaniu
a prostej o równaniu
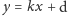 odpowiada punkt
o współrzędnych
odpowiada punkt
o współrzędnych
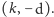 Punkty i proste oraz ich obrazy leżą
w płaszczyźnie
Punkty i proste oraz ich obrazy leżą
w płaszczyźnie
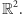 Płaszczyznę, z której bierzemy argumenty
przekształcenia
Płaszczyznę, z której bierzemy argumenty
przekształcenia
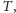 nazywamy przestrzenią pierwotną, natomiast
płaszczyznę, w której znajdują się jego wartości – przestrzenią dualną. Opisane
przekształcenie ma bardzo ciekawą właściwość: punkt
nazywamy przestrzenią pierwotną, natomiast
płaszczyznę, w której znajdują się jego wartości – przestrzenią dualną. Opisane
przekształcenie ma bardzo ciekawą właściwość: punkt
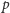 leży na
prostej
leży na
prostej
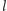 wtedy i tylko wtedy, gdy prosta
wtedy i tylko wtedy, gdy prosta
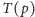 przechodzi przez
punkt
przechodzi przez
punkt
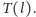
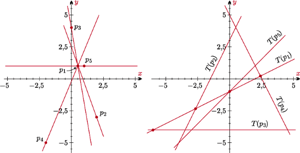
Rys. 2 Przestrzeń pierwotna (po lewej) oraz odpowiadająca jej przestrzeń dualna (po prawej). |
Rys. 3 Wszystkie proste z rysunku 1 |
Zbiór punktów
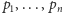 oraz prostych łączących je w pary możemy
odwzorować w zbiór prostych
oraz prostych łączących je w pary możemy
odwzorować w zbiór prostych
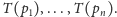 W przestrzeni
dualnej proste, które łączą np.
W przestrzeni
dualnej proste, które łączą np.
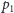 z pozostałymi punktami,
odpowiadają punktom przecięć prostej
z pozostałymi punktami,
odpowiadają punktom przecięć prostej
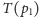 z prostymi
z prostymi
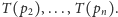 Od tej własności jest jednak mały wyjątek. Gdy
pewne punkty
Od tej własności jest jednak mały wyjątek. Gdy
pewne punkty
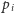 i
i
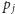 mają tę samą pierwszą współrzędną, to
w przestrzeni dualnej proste
mają tę samą pierwszą współrzędną, to
w przestrzeni dualnej proste
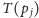 oraz
oraz
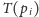 będą równoległe.
Taką sytuacją zajmiemy się jednak za chwilę.
będą równoległe.
Taką sytuacją zajmiemy się jednak za chwilę.
Dotarliśmy zatem do następującego problemu. Danych jest
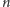 prostych na
płaszczyźnie. Dla każdej prostej należy obliczyć, w jakiej kolejności
(względem pierwszej współrzędnej) będą się z nią przecinały pozostałe proste.
Z konstrukcji przestrzeni dualnej wynika, że żadna prosta nie będzie pionowa.
Znając porządek przecięć dla prostej
prostych na
płaszczyźnie. Dla każdej prostej należy obliczyć, w jakiej kolejności
(względem pierwszej współrzędnej) będą się z nią przecinały pozostałe proste.
Z konstrukcji przestrzeni dualnej wynika, że żadna prosta nie będzie pionowa.
Znając porządek przecięć dla prostej
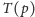 w przestrzeni dualnej,
możemy odtworzyć porządek prostych przechodzących przez punkt
w przestrzeni dualnej,
możemy odtworzyć porządek prostych przechodzących przez punkt
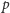 w przestrzeni pierwotnej, a z niego porządek biegunowy wszystkich
punktów względem
w przestrzeni pierwotnej, a z niego porządek biegunowy wszystkich
punktów względem
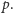
Jak wykonać ostatni z tych kroków? Wystarczy dwa razy przejrzeć proste
w niemalejącej kolejności współczynników kierunkowych i przy
pierwszym przejściu wypisać tylko punkty leżące na lewo od
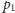 (tj.
mające mniejszą pierwszą współrzędną), a przy drugim przejściu –
wypisać pozostałe. Musimy jeszcze osobno rozważyć wszystkie punkty
mające tę samą pierwszą współrzędną co
(tj.
mające mniejszą pierwszą współrzędną), a przy drugim przejściu –
wypisać pozostałe. Musimy jeszcze osobno rozważyć wszystkie punkty
mające tę samą pierwszą współrzędną co
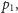 jednak bardzo łatwo
możemy umieścić je w odpowiednim miejscu w porządku biegunowym
wokół
jednak bardzo łatwo
możemy umieścić je w odpowiednim miejscu w porządku biegunowym
wokół
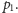 Ten proces powtarzamy dla każdego punktu wśród
Ten proces powtarzamy dla każdego punktu wśród
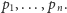
Rys. 4 Struktura danych u dołu reprezentuje układ odcinków przedstawiony u góry. Został on zbudowany przez otoczenie prostokątną ramką prostych z rysunku 3
Wyznaczanie przecięć prostych
Spójrzmy na rysunek 4 Przedstawia on strukturę danych, która reprezentuje układ odcinków stykających się jedynie końcami. Co więcej, każdy koniec odcinka jest jednocześnie końcem jakiegoś innego odcinka. Każdy punkt styku reprezentujemy za pomocą listy cyklicznej. Element listy odpowiada końcowi odcinka i oprócz wskaźników do następnika i poprzednika zawiera także wskaźnik do elementu innej listy, który reprezentuje drugi koniec tego samego odcinka. Ponadto elementy listy reprezentującej punkt styku zawierają jego współrzędne. Kolejność elementów na liście jest istotna i musi odpowiadać kolejności występowania odcinków na płaszczyźnie, na przykład być zgodna z kierunkiem ruchu wskazówek zegara.

Rys. 5 Fazy dodawania prostej do struktury danych.
Opisana struktura jest wariantem tzw. doubly-connected edge list. Pozwala ona szybko dodawać nowe odcinki do istniejącego układu. Zauważmy też, że dzięki wskaźnikom do sąsiedniego odcinka oraz dzięki odpowiedniemu uporządkowaniu elementów na listach cyklicznych, odpowiadających punktom styku, możemy w prosty sposób obchodzić dookoła obszary (ściany) wyznaczone przez układ odcinków. Rysunek 5 przedstawia kolejne fazy dodawania odcinków prostej do układu.
Operacje na strukturze są dosyć intuicyjne. Nas interesuje odpowiedź na pytanie,
jaki jest ich czas działania względem
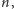 bo od tego zależy złożoność
algorytmu. Widać, że nowo powstająca ściana może mieć bardzo wiele
krawędzi, nawet liniowo wiele względem
bo od tego zależy złożoność
algorytmu. Widać, że nowo powstająca ściana może mieć bardzo wiele
krawędzi, nawet liniowo wiele względem
 Okazuje się jednak, że
sumaryczna liczba krawędzi, które trzeba odwiedzić przy dodawaniu
odcinków jednej prostej, jest również rzędu
Okazuje się jednak, że
sumaryczna liczba krawędzi, które trzeba odwiedzić przy dodawaniu
odcinków jednej prostej, jest również rzędu
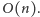 Dowód tego faktu
pominiemy, choć nie jest bardzo trudny. Opiera się on na obserwacji, że
odwiedzane krawędzie można przyporządkować do punktów przecięć
przetwarzanej prostej w ten sposób, by na jeden punkt przypadało co najwyżej
10 krawędzi. Zainteresowani dowodem powinni szukać hasła twierdzenie
strefowe lub zone theorem.
Dowód tego faktu
pominiemy, choć nie jest bardzo trudny. Opiera się on na obserwacji, że
odwiedzane krawędzie można przyporządkować do punktów przecięć
przetwarzanej prostej w ten sposób, by na jeden punkt przypadało co najwyżej
10 krawędzi. Zainteresowani dowodem powinni szukać hasła twierdzenie
strefowe lub zone theorem.
Powyższy fakt jest kluczowy dla analizy złożoności czasowej algorytmu, bo
wynika z niego, że strukturę daje się zbudować w czasie
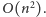 Ponadto
przejście po kolejnych odcinkach jednej prostej można zrealizować w czasie
Ponadto
przejście po kolejnych odcinkach jednej prostej można zrealizować w czasie
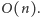 Zauważmy, że jeżeli zbiór punktów
Zauważmy, że jeżeli zbiór punktów
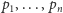 na
płaszczyźnie przekształcimy za pomocą dualizacji na zbiór prostych
na
płaszczyźnie przekształcimy za pomocą dualizacji na zbiór prostych
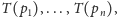 a te proste otoczymy ramką, to otrzymamy układ
odcinków podobny do tego z rysunku 4
a te proste otoczymy ramką, to otrzymamy układ
odcinków podobny do tego z rysunku 4
Prostokątną ramkę, obejmującą wszystkie punkty przecięcia układu
 prostych, możemy obliczyć następująco. Sortujemy (w czasie
prostych, możemy obliczyć następująco. Sortujemy (w czasie
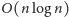 ) wszystkie proste względem ich współczynników
kierunkowych i bierzemy pod uwagę tylko punkty przecięć prostych
sąsiadujących w tym porządku oraz punkt przecięcia pierwszej i ostatniej
prostej. Wszystkie pozostałe punkty przecięć znajdują się wewnątrz otoczki
wypukłej tych punktów.
) wszystkie proste względem ich współczynników
kierunkowych i bierzemy pod uwagę tylko punkty przecięć prostych
sąsiadujących w tym porządku oraz punkt przecięcia pierwszej i ostatniej
prostej. Wszystkie pozostałe punkty przecięć znajdują się wewnątrz otoczki
wypukłej tych punktów.
Dalej, za pomocą opisanego powyżej algorytmu konstrukcji struktury
doubly-connected edge list jesteśmy w stanie w czasie
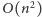 wyznaczyć
kolejność punktów przecięć dla wszystkich prostych. Jeśli teraz dla
dowolnego punktu z
wyznaczyć
kolejność punktów przecięć dla wszystkich prostych. Jeśli teraz dla
dowolnego punktu z
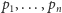 (np.
(np.
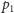 ) zapragniemy wyznaczyć
porządek biegunowy pozostałych punktów
) zapragniemy wyznaczyć
porządek biegunowy pozostałych punktów
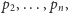 to wystarczy
odczytać porządek przecięć prostej
to wystarczy
odczytać porządek przecięć prostej
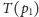 z pozostałymi prostymi.
Numery prostych w tym porządku wyznaczą kolejność punktów
z pozostałymi prostymi.
Numery prostych w tym porządku wyznaczą kolejność punktów
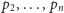 w porządku biegunowym dookoła
w porządku biegunowym dookoła
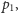 o czym
pisaliśmy powyżej.
o czym
pisaliśmy powyżej.
Za pomocą dualizacji udało nam się przyspieszyć algorytm sortowania
biegunowego zbioru
 punktów z czasu
punktów z czasu
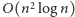 do czasu
do czasu
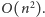 Usprawnienie to nie ma dużego znaczenia w przypadku np.
zadań opisywanych w Informatycznym Kąciku Olimpijskim, ponieważ jego
implementacja jest bardzo skomplikowana, a przyspieszenia raczej nie dałoby się
zauważyć na zbiorach danych o stosunkowo niewielkim rozmiarze.
Przyspieszanie takich algorytmów ma jednak rację bytu w poważniejszych
zastosowaniach geometrii obliczeniowej, takich jak generowanie grafiki lub
projektowanie układów scalonych.
Usprawnienie to nie ma dużego znaczenia w przypadku np.
zadań opisywanych w Informatycznym Kąciku Olimpijskim, ponieważ jego
implementacja jest bardzo skomplikowana, a przyspieszenia raczej nie dałoby się
zauważyć na zbiorach danych o stosunkowo niewielkim rozmiarze.
Przyspieszanie takich algorytmów ma jednak rację bytu w poważniejszych
zastosowaniach geometrii obliczeniowej, takich jak generowanie grafiki lub
projektowanie układów scalonych.
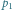 oraz porządek biegunowy punktów względem
oraz porządek biegunowy punktów względem