Co to jest?
Marian Smoluchowski
Pudełko Smoluchowskiego, losowe ruchy w grafie i egzopeptydazy
Marian Ritter von Smolan Smoluchowski - światowej sławy polski fizyk, pionier fizyki statystycznej, alpinista i taternik, żył w latach 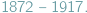 Egzopeptydazy to specjalny typ enzymów. Co może mieć wspólnego Smoluchowski z egzopeptydazami, skoro ani on, ani nikt z jego współczesnych nie wiedzieli o ich istnieniu? I co do tego mają grafy? Postaram się wszystko wyjaśnić w odpowiedniej kolejności. Zacznę od uproszczonego modelu fizycznego. Podobno zbliżony model rozpatrywał Smoluchowski, ale, niestety, nie udało mi się dotrzeć do źródeł i sprawdzić tej informacji.
Egzopeptydazy to specjalny typ enzymów. Co może mieć wspólnego Smoluchowski z egzopeptydazami, skoro ani on, ani nikt z jego współczesnych nie wiedzieli o ich istnieniu? I co do tego mają grafy? Postaram się wszystko wyjaśnić w odpowiedniej kolejności. Zacznę od uproszczonego modelu fizycznego. Podobno zbliżony model rozpatrywał Smoluchowski, ale, niestety, nie udało mi się dotrzeć do źródeł i sprawdzić tej informacji.

Wyobraźmy sobie "pudełko" (określony obszar przestrzeni), do którego losowo wpadają cząstki i z którego losowo wypadają. Mówiąc nieco dokładniej, zakładamy, że w "krótkim" odcinku czasu, powiedzmy ![[t,t+ h],](/math/temat/fizyka/fizyka_statystyczna/2015/03/29/Pudelko_Smoluchowskiego/1x-608dd0c6d04c2aa808489ce9d23c65bb2a41d4d9-im-33,33,33-FF,FF,FF.gif)
- do pudełka wpada 1 cząstka z prawdopodobieństwem w przybliżeniu równym
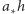 ; prawdopodobieństwo wpadnięcia 2 lub więcej cząstek jest tak małe, że możemy je zaniedbać,
; prawdopodobieństwo wpadnięcia 2 lub więcej cząstek jest tak małe, że możemy je zaniedbać, - każda spośród cząstek znajdujących się w pudełku wypada z niego z prawdopodobieństwem w przybliżeniu równym
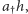 niezależnie od pozostałych cząstek.
niezależnie od pozostałych cząstek.
Żeby to sformułować jeszcze dokładniej, wprowadzimy wygodną terminologię i kilka oznaczeń. Zamiast mówić "w pudełku jest 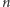 cząstek", powiemy, że "układ znajduje się w stanie
cząstek", powiemy, że "układ znajduje się w stanie 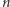 ". Niech
". Niech 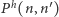 oznacza prawdopodobieństwo tego, że układ w chwili
oznacza prawdopodobieństwo tego, że układ w chwili 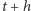 będzie w stanie
będzie w stanie 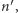 jeśli w chwili
jeśli w chwili 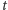 jest w stanie
jest w stanie 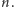 Rozumie się, że
Rozumie się, że 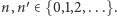 Załóżmy istnienie granic
Załóżmy istnienie granic
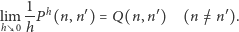 |
(1) |
Nazwiemy 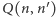 intensywnością przejścia z
intensywnością przejścia z  do
do 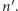 Ścisłe sformułowanie założeń modelu Smoluchowskiego jest takie:
Ścisłe sformułowanie założeń modelu Smoluchowskiego jest takie:
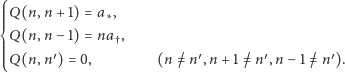 |
(2) |
Układ znajduje się w równowadze, jeśli prawdopodobieństwa poszczególnych stanów nie zmieniają się w czasie (mówimy tu o równowadze probabilistycznej, która nie oznacza bezruchu, tylko zrównoważone losowe fluktuacje). Niech 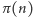 będzie prawdopodobieństwem stanu
będzie prawdopodobieństwem stanu  Ogólny warunek równowagi jest następujący:
Ogólny warunek równowagi jest następujący:
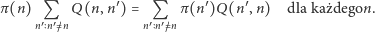 |
(3) |
Wzór (3) mówi tyle, że prawdopodobieństwo wyjścia ze stanu 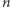 jest równe prawdopodobieństwu wejścia do stanu
jest równe prawdopodobieństwu wejścia do stanu  Jeśli rozkład prawdopodobieństwa
Jeśli rozkład prawdopodobieństwa 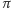 spełnia (3), to mówimy, że jest rozkładem równowagi lub inaczej stacjonarnym. Chwila zastanowienia wystarczy, żeby zrozumieć, że to dobra definicja. Silniejszy od ogólnego warunku równowagi jest następujący warunek równowagi szczegółowej:
spełnia (3), to mówimy, że jest rozkładem równowagi lub inaczej stacjonarnym. Chwila zastanowienia wystarczy, żeby zrozumieć, że to dobra definicja. Silniejszy od ogólnego warunku równowagi jest następujący warunek równowagi szczegółowej:
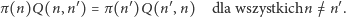 |
(4) |
Pozostawiamy Czytelnikowi łatwe sprawdzenie, że (4) implikuje (3). Warunek (4) można interpretować jako odwracalność w czasie. Film, pokazujący stan układu, powiedzmy 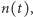 w pewnym odcinku czasu,
w pewnym odcinku czasu, ![|t∈ [t0,t1],](/math/temat/fizyka/fizyka_statystyczna/2015/03/29/Pudelko_Smoluchowskiego/27x-608dd0c6d04c2aa808489ce9d23c65bb2a41d4d9-im-33,33,33-FF,FF,FF.gif) wygląda tak samo, jak tenże film "puszczony wspak":
wygląda tak samo, jak tenże film "puszczony wspak": 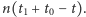 To dlatego, że przejścia
To dlatego, że przejścia 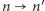 zdarzają się jednakowo często jak przejścia
zdarzają się jednakowo często jak przejścia 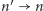 (przy równowagowym rozkładzie prawdopodobieństwa
(przy równowagowym rozkładzie prawdopodobieństwa 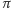 ).
).
Zastanówmy się, jaki jest rozkład równowagi w modelu Smoluchowskiego. Odpowiedź jest łatwa, jeśli wpadniemy na pomysł, żeby szukać rozkładu 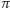 spełniającego warunek równowagi szczegółowej. Istotnie, jeśli zachodzi (4), to
spełniającego warunek równowagi szczegółowej. Istotnie, jeśli zachodzi (4), to

Stąd 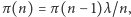 gdzie
gdzie 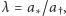 a więc
a więc

Aby wyznaczyć stałą 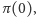 wystarczy skorzystać z oczywistego równania
wystarczy skorzystać z oczywistego równania 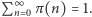 Ponieważ
Ponieważ 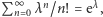 więc
więc 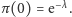 Otrzymaliśmy następujący wynik.
Otrzymaliśmy następujący wynik.
Twierdzenie 1. W modelu Smoluchowskiego rozkład prawdopodobieństwa dany wzorem

jest rozkładem równowagi.
Można pokazać, że wychodząc z dowolnego stanu początkowego, w długim okresie czasu zbliżamy się do rozkładu równowagi: 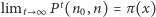 dla wszystkich
dla wszystkich 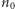 i
i 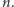 Sławny rozkład występujący w Twierdzeniu 1 związany jest (jak wiele innych wspaniałych obiektów matematycznych) z nazwiskiem francuskiego fizyka i matematyka Siméona Denisa Poissona
Sławny rozkład występujący w Twierdzeniu 1 związany jest (jak wiele innych wspaniałych obiektów matematycznych) z nazwiskiem francuskiego fizyka i matematyka Siméona Denisa Poissona  Zastanówmy się, jaka jest średnia liczba cząstek w pudełku Smoluchowskiego (znajdującym się w równowadze). Jeśli tę średnią liczbę oznaczymy chwilowo przez
Zastanówmy się, jaka jest średnia liczba cząstek w pudełku Smoluchowskiego (znajdującym się w równowadze). Jeśli tę średnią liczbę oznaczymy chwilowo przez 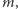 to możemy przeprowadzić następujące rozumowanie. W krótkim okresie długości
to możemy przeprowadzić następujące rozumowanie. W krótkim okresie długości 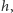 w przybliżeniu,
w przybliżeniu,
- do pudełka wpada średnio
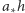 cząstek,
cząstek, - z pudełka wypada średnio
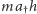 cząstek.
cząstek.
Ponieważ średnio tyle samo cząstek wpada, co wypada (równowaga!) to 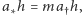 skąd
skąd 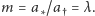 Tak więc zmienna losowa o rozkładzie Poissona ma wartość średnią (nieszczęśliwie nazywaną też "wartością oczekiwaną") równą
Tak więc zmienna losowa o rozkładzie Poissona ma wartość średnią (nieszczęśliwie nazywaną też "wartością oczekiwaną") równą 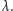 Koledzy matematycy nie uznają tego rozumowania za dowód, ale moim zdaniem to ciekawe wyprowadzenie.
Koledzy matematycy nie uznają tego rozumowania za dowód, ale moim zdaniem to ciekawe wyprowadzenie.
Zwróćmy uwagę na zaskakujący fakt. Ponieważ model (2) spełnia warunek (4), to jest on odwracalny w czasie. Oglądając nasze pudełko znajdujące się w równowadze probabilistycznej, nie mamy możliwości rozpoznania, w którym kierunku płynie czas.
- Cały artykuł dostępny jest w wersji do druku [application/pdf]: (702 KB)