Pierścień Kaca
Charakterystyczną cechą układów makroskopowych, złożonych z wielkiej liczby cząsteczek jest to, że zachodzą w nich procesy nieodwracalne, takie jak przepływ ciepła pomiędzy ciałami o różnych temperaturach. Dzieje się tak, mimo że prawa mechaniki klasycznej, rządzące ruchem cząsteczek, są odwracalne w czasie.
Wprawdzie „natura” cząsteczek jest kwantowa, ale ich ruch pomiędzy zderzeniami można opisać klasycznie, o ile energia nie jest zbyt wysoka. Samo zderzenie cząsteczek należy opisywać prawami mechaniki kwantowej, ale jedyną wielkością, której potrzebujemy w analizie ich ruchu, jest tak zwany przekrój czynny na zderzenie, czyli – mówiąc niezbyt dokładnie – prawdopodobieństwo zderzenia. Najczęściej jednak traktujemy cząsteczki jako sztywne kule zderzające się sprężyście, bez wnikania w to, co dzieje się z nimi, gdy znajdą się bardzo blisko. Jeśli potraktujemy cząsteczki jako klasyczne sztywne kule, obliczenie przekroju czynnego na zderzenie jest zadaniem trywialnym. Sprzeczność między nieodwracalnością wielu fizycznych procesów a odwracalnością praw mechaniki klasycznej nosi nazwę paradoksu Loschmita. Co więcej, z twierdzenia Poincarégo o powrocie wynika, że dla prawie wszystkich stanów początkowych układ powróci w pobliże stanu początkowego, choć dla układów makroskopowych ten czas powrotu jest niesłychanie duży (większy niż czas życia Wszechświata). Porównanie konsekwencji twierdzenia Poincarégo z istnieniem procesów nieodwracalnych nazwano paradoksem Zermelo. Z obu paradoksów płynie wniosek, że nieodwracalności procesów w makroskopowych układach nie można wytłumaczyć w kategoriach czysto mechanicznych (niezbędne są pewne założenia o charakterze statystycznym), a poza tym nieodwracalność nie ma charakteru bezwzględnego, lecz związana jest z właściwą układowi skalą czasu. Należy wspomnieć, że twierdzenie Poincarégo dotyczy zachowawczych (izolowanych) układów mechanicznych, natomiast układy, z którymi mamy do czynienia w rzeczywistości, nie są izolowane, jednak nie tu tkwi istota rzeczy.
Dążenie makroskopowego układu do stanu równowagi – co jest procesem
nieodwracalnym – w przypadku rozrzedzonego gazu opisywane jest
równaniem Boltzmanna. Jednak analiza zachowania się wielkiego zbioru
cząsteczek poruszających się w trójwymiarowej przestrzeni jest niesłychanie
trudna, dlatego uprościmy sobie zadanie i przedyskutujemy własności
bardzo prostego modelu, mającego wszystkie interesujące nas własności,
zaproponowanego przez Marka Kaca. Model ten został nazwany pierścieniem
Kaca. Rozważymy zatem okrąg podzielony przez
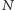 punktów
na
punktów
na
 komórek, każda z nich zawiera kulkę białą lub czarną, założymy
przy tym, że w stanie początkowym dominują kulki jednego koloru.
W jednostkowych odstępach czasu każda z kulek przeskakuje do następnej
komórki, umówmy się, że zgodnie z ruchem wskazówek zegara. Pewna
liczba punktów zawiera wskaźniki, które zmieniają kolor mijającej
wskaźnik kulki. Przejście kulki przez znacznik jest tu odpowiednikiem
zderzenia cząsteczek. Spodziewalibyśmy się, że układ dąży do stanu
równowagi, w którym liczba białych kulek jest równa liczbie kulek
czarnych.
komórek, każda z nich zawiera kulkę białą lub czarną, założymy
przy tym, że w stanie początkowym dominują kulki jednego koloru.
W jednostkowych odstępach czasu każda z kulek przeskakuje do następnej
komórki, umówmy się, że zgodnie z ruchem wskazówek zegara. Pewna
liczba punktów zawiera wskaźniki, które zmieniają kolor mijającej
wskaźnik kulki. Przejście kulki przez znacznik jest tu odpowiednikiem
zderzenia cząsteczek. Spodziewalibyśmy się, że układ dąży do stanu
równowagi, w którym liczba białych kulek jest równa liczbie kulek
czarnych.
Naszym celem jest znalezienie równań opisujących liczbę kulek białych
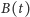 i czarnych
i czarnych
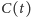 jako funkcji (dyskretnego, mierzonego
liczbami naturalnymi) czasu
jako funkcji (dyskretnego, mierzonego
liczbami naturalnymi) czasu
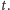 Oznaczmy przez
Oznaczmy przez
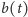 i
i
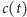 liczby białych i czarnych kulek znajdujących się bezpośrednio przed
znacznikami, a więc zmieniających kolor w najbliższym skoku.
liczby białych i czarnych kulek znajdujących się bezpośrednio przed
znacznikami, a więc zmieniających kolor w najbliższym skoku.
Spełnione są równania
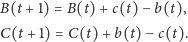 | (1) |
Oznaczmy przez
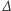 różnicę między liczbą białych i czarnych kulek.
Spełnia ona równanie
różnicę między liczbą białych i czarnych kulek.
Spełnia ona równanie
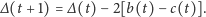 | (2) |
Jest to równanie wprawdzie ścisłe, ale zupełnie bezwartościowe, nie znamy
bowiem rozkładu kulek przed znacznikami. Wprowadzimy do modelu
pewne założenie statystyczne. Założymy mianowicie, że ułamek cząstek
zmieniających barwę w danym kroku jest równy prawdopodobieństwu
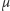 tego, że wybrany punkt dzielący okrąg na komórki jest znacznikiem.
Prawdopodobieństwo to możemy zdefiniować jako stosunek liczby
znaczników do liczby wszystkich punktów. A zatem
tego, że wybrany punkt dzielący okrąg na komórki jest znacznikiem.
Prawdopodobieństwo to możemy zdefiniować jako stosunek liczby
znaczników do liczby wszystkich punktów. A zatem
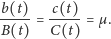 | (3) |
Przy tym założeniu równanie (2) daje się sprowadzić do postaci
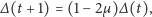 | (4) |
które można iterować
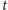 razy, aby otrzymać rozwiązanie w postaci
razy, aby otrzymać rozwiązanie w postaci
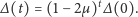 | (5) |
W nieciekawym przypadku
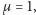 kiedy w każdym punkcie znajduje się
znacznik, w każdym ruchu każda kulka zmienia kolor, a zatem obserwujemy
oscylacje,
kiedy w każdym punkcie znajduje się
znacznik, w każdym ruchu każda kulka zmienia kolor, a zatem obserwujemy
oscylacje,
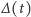 zmienia jedynie znak, co także odzwierciedla wzór 5.
Jednak gdy
zmienia jedynie znak, co także odzwierciedla wzór 5.
Jednak gdy
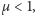 rozwiązanie, które otrzymaliśmy, odpowiada
znikającej różnicy ilości białych i czarnych kulek (
rozwiązanie, które otrzymaliśmy, odpowiada
znikającej różnicy ilości białych i czarnych kulek (
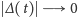 ), gdy
), gdy
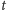 dąży do nieskończoności, co zgadza się z obserwowanym
w przyrodzie dążeniem do stanu równowagi; takie zachowanie się układu
nazwiemy boltzmannowskim. Z drugiej strony nasz wynik w oczywisty sposób
jest błędny, ponieważ mamy
dąży do nieskończoności, co zgadza się z obserwowanym
w przyrodzie dążeniem do stanu równowagi; takie zachowanie się układu
nazwiemy boltzmannowskim. Z drugiej strony nasz wynik w oczywisty sposób
jest błędny, ponieważ mamy
1. Paradoks Loschmita: równanie 4 i jego rozwiązanie 5 nie jest niezmiennicze względem odwrócenia czasu, podczas gdy dynamika układu jest odwracalna.
2. Paradoks Zermelo: w czasie
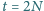 każda z kulek dwukrotnie mija
każdy znacznik, a więc układ musi wrócić do pierwotnego stanu
(twierdzenie Poincarégo o powrocie).
każda z kulek dwukrotnie mija
każdy znacznik, a więc układ musi wrócić do pierwotnego stanu
(twierdzenie Poincarégo o powrocie).
Dokładniej rzecz biorąc, zarówno równanie (4), jak i rozwiązanie (5) wcale
nie muszą być złe, jedynie zakres ich stosowalności jest ograniczony.
Sprzeczność między nieodwracalnym charakterem obserwowanych zjawisk
i odwracalnością dynamiki, jak również paradoksy Loschmita i Zermelo
zostają rozwiązane, jeśli wprowadzimy zespół statystyczny i wykażemy, że
równania (4, 5) opisują nie ścisłe zachowanie się dowolnego układu w zespole,
lecz najbardziej prawdopodobne zachowanie się jednego z układów tworzących
zespół. Zespół statystyczny zdefiniujemy jako zbiór pierścieni Kaca
o tym samym początkowym rozmieszczeniu kulek czarnych i białych,
ale o różnych rozmieszczeniach tej samej liczby znaczników. Niech
 oznacza numer punktu, natomiast ułamek układów mających znacznik
w punkcie
oznacza numer punktu, natomiast ułamek układów mających znacznik
w punkcie
 jest równy
jest równy
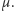 Stan mikroskopowy układu opiszemy
następująco:
Stan mikroskopowy układu opiszemy
następująco:

Posługując się tymi definicjami, możemy napisać
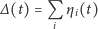 | (6) |
oraz
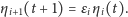 | (7) |
Możemy więc wyrazić
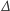 przez warunki początkowe
przez warunki początkowe
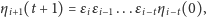 | (8) |
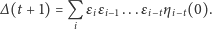 | (9) |
Odnotujmy, że
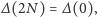 ponieważ po czasie
ponieważ po czasie
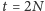 każdy
z epsilonów pojawia się dwukrotnie. Uśrednijmy to wyrażenie względem
zespołu.
każdy
z epsilonów pojawia się dwukrotnie. Uśrednijmy to wyrażenie względem
zespołu.
 | (10) |
Po prawej stronie równania (10) mamy średnią iloczynu
 kolejnych
epsilonów. Średnia iloczynu epsilonów nie zależy od
kolejnych
epsilonów. Średnia iloczynu epsilonów nie zależy od
 więc
możemy wyciągnąć ją przed sumę, a że są to kolejne epsilony, możemy
ponumerować je od
więc
możemy wyciągnąć ją przed sumę, a że są to kolejne epsilony, możemy
ponumerować je od
 do
do
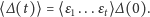 | (11) |
Przedyskutujemy dwa przypadki, gdy
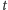 jest mniejsze i gdy jest większe
niż
jest mniejsze i gdy jest większe
niż
 Prawdopodobieństwo tego, że kulka mija
Prawdopodobieństwo tego, że kulka mija
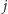 znaczników
w
znaczników
w
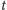 krokach, jest równe iloczynowi
krokach, jest równe iloczynowi
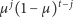 |
(jest to prawdopodobieństwo wystąpienia
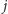 znaczników w dowolnym
układzie) przez
znaczników w dowolnym
układzie) przez
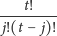 |
(jest to ilość możliwych rozmieszczeń
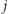 znaczników pośród
znaczników pośród
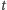 punktów). Dla
punktów). Dla
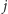 znaczników iloczyn epsilonów jest równy
znaczników iloczyn epsilonów jest równy
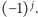 Mamy zatem dla
Mamy zatem dla
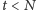
 | (12) |
(W oryginalnej pracy Kaca ta średnia obliczona jest w zupełnie inny, niezwykle
pomysłowy, choć trudniejszy sposób.) Powyższa procedura jest poprawna
pod warunkiem, że
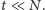 Duże wartości
Duże wartości
 w sumie
(12) mogą być większe od ilości znaczników i takie składniki sumy
fałszują wynik. Wynik, który otrzymaliśmy, natychmiast prowadzi
do wniosku
w sumie
(12) mogą być większe od ilości znaczników i takie składniki sumy
fałszują wynik. Wynik, który otrzymaliśmy, natychmiast prowadzi
do wniosku
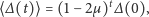 | (13) |
przy czym jest on prawdziwy, gdy
 jest mniejsze nie tylko od
jest mniejsze nie tylko od
 lecz i od liczby znaczników. Jest to wynik zgodny z równaniem opartym
na założeniu (3), tyle tylko, że opisuje on nie dokładne zachowanie się
pojedynczego układu (z całego zespołu możliwych układów), lecz najbardziej
prawdopodobne zachowanie się jednego z układów w zespole. Dla
lecz i od liczby znaczników. Jest to wynik zgodny z równaniem opartym
na założeniu (3), tyle tylko, że opisuje on nie dokładne zachowanie się
pojedynczego układu (z całego zespołu możliwych układów), lecz najbardziej
prawdopodobne zachowanie się jednego z układów w zespole. Dla
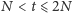 zapiszemy
zapiszemy

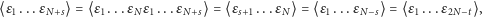 | (14) |
gdzie najpierw pozbyliśmy się znaczników występujących dwukrotnie,
a potem inaczej ponumerowaliśmy punkty. Dostajemy wynik taki sam jak
poprzednio, tylko zamiast
 mamy
mamy
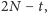
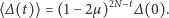 | (15) |
Wynik ten jest poprawny, gdy
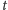 jest bliskie wartości
jest bliskie wartości
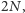 z podobnych
powodów jak w poprzednim przypadku. Gdy
z podobnych
powodów jak w poprzednim przypadku. Gdy
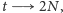 średnia po
zespole dąży do wartości początkowej. Nazwiemy to antyboltzmannowskim
zachowaniem się układu.
średnia po
zespole dąży do wartości początkowej. Nazwiemy to antyboltzmannowskim
zachowaniem się układu.
Wykazaliśmy zatem, że typowy układ będzie dążył do stanu równowagi,
w którym liczba czarnych kulek jest równa liczbie białych kulek i że jest to
typowe zachowanie się tylko w pewnej skali czasu. Co więcej, można
wykazać, że odchylenie standardowe maleje wraz z
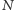 zgodnie
z prawem
zgodnie
z prawem
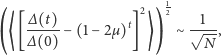 | (16) |
co oznacza, że w dużym zespole statystycznym większość układów
zachowuje się (w odpowiedniej skali czasu) po boltzmannowsku. Nie wyklucza
to faktu, że mogą istnieć w zespole także inne, bardzo szczególne
układy, które zachowują się w sposób zupełnie inny niż średnie
opisane powyżej, na przykład gdy znaczniki rozmieścimy na okręgu
regularnie. Jeśli znacznik znajduje się w co drugim punkcie (wymaga to,
by
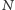 było liczbą parzystą), to po dwóch skokach każda kulka
dwukrotnie zmienia kolor, czyli układ wraca do stanu sprzed dwóch skoków,
zachowując się periodycznie z okresem 2. Nie jest to ani boltzmannowskie, ani
antyboltzmannowskie zachowanie się układu. Czytelnik bez trudu sam znajdzie
inne przykłady. Jednak są to zawsze bardzo nieliczne w zespole układy.
Zdecydowana większość układów zachowuje się w sposób bliski
średniej.
było liczbą parzystą), to po dwóch skokach każda kulka
dwukrotnie zmienia kolor, czyli układ wraca do stanu sprzed dwóch skoków,
zachowując się periodycznie z okresem 2. Nie jest to ani boltzmannowskie, ani
antyboltzmannowskie zachowanie się układu. Czytelnik bez trudu sam znajdzie
inne przykłady. Jednak są to zawsze bardzo nieliczne w zespole układy.
Zdecydowana większość układów zachowuje się w sposób bliski
średniej.