Proca grawitacyjna
Kiedy podrzucamy piłkę do góry, to przyciąganie grawitacyjne zawsze ją zawraca. Im mocniej ją podrzucimy -- czyli im większą nadamy jej energię -- tym wyżej poleci, zanim zawróci. Ale czy zawsze zawróci?
Nadanie obiektowi wystarczająco dużej prędkości początkowej (większej od
pewnej granicznej wartości zwanej prędkością ucieczki) pozwala mu uwolnić
się z przywiązania do Ziemi i odlecieć na dowolnie dużą odległość.
Przyciąganie Ziemi nigdy nie zdoła zawrócić takiego obiektu. Prędkość
ucieczki z powierzchni Ziemi to około
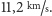
Mimo, że jest to dosyć duża prędkość (kilkukrotnie większa niż np. prędkość pocisku wystrzelonego z karabinu lub działa – dlatego pociski zawsze spadają na Ziemię), to ludzkość zbudowała pojazdy zdolne ją osiągać. Na przykład, przekroczył ją statek Apollo 11, którego załoga 45 lat temu, dokładnie 20 lipca, wylądowała na Księżycu. Rakiety Saturn V, wynoszące statki Apollo, były najpotężniejszymi zbudowanymi kiedykolwiek rakietami.
Chcąc lecieć dalej w Kosmos, napotkamy kolejną, większą przeszkodę. Dużo
trudniejsze od ucieczki z Ziemi jest wyzwolenie się ze studni potencjału
grawitacyjnego Słońca. Prędkość ucieczki względem grawitacji Słońca
z punktu położonego na orbicie Ziemi wynosi około
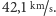 Żaden ze
zbudowanych do tej pory przez człowieka pojazdów kosmicznych nie był
w stanie za pomocą własnych silników nadać sobie energii wystarczającej do
ucieczki od Słońca. Wiadomo jednak, że kilka wysłanych z Ziemi sond
opuściło Układ Słoneczny na dobre – przyciąganie Słońca nigdy ich już nie
zawróci. Jak im się to zatem udało?
Żaden ze
zbudowanych do tej pory przez człowieka pojazdów kosmicznych nie był
w stanie za pomocą własnych silników nadać sobie energii wystarczającej do
ucieczki od Słońca. Wiadomo jednak, że kilka wysłanych z Ziemi sond
opuściło Układ Słoneczny na dobre – przyciąganie Słońca nigdy ich już nie
zawróci. Jak im się to zatem udało?
Rozpędzenie sondy uzyskano dzięki sprytnemu zaplanowaniu trajektorii lotu, tak aby w odpowiedni sposób przeleciała w pobliżu planety Układu Słonecznego i ukradła jej trochę energii. Mechanizm ten nosi nazwę procy grawitacyjnej lub asysty grawitacyjnej i był wykorzystywany do rozpędzania wielu sond, a niektóre z nich wykorzystywały go kilkakrotnie w czasie swojej misji, przelatując w pobliżu różnych planet lub zbliżając się kilka razy do tej samej. Jak to działa?
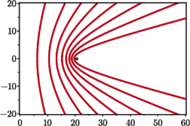
Rys. 1 Orbity hiperboliczne. Wszystkie hiperbole na rysunku mają wspólne ognisko, w którym znajduje się planeta.
Rys. 2 Przelot sondy w pobliżu planety widziany w układzie odniesienia związanym z planetą.
 – prędkość planety względem Słońca,
– prędkość planety względem Słońca,
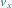 – składowa prędkości sondy
względem Słońca równoległa do prędkości planety,
– składowa prędkości sondy
względem Słońca równoległa do prędkości planety,
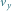 – składowa prędkości sondy
prostopadła do prędkości planety.
– składowa prędkości sondy
prostopadła do prędkości planety.

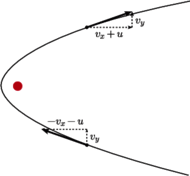
Rys. 3 Przelot sondy w pobliżu planety w układzie odniesienia Słońca.
Wyobraźmy sobie, że sonda zbliża się do planety. W układzie odniesienia związanym z planetą, trajektoria sondy jest w przybliżeniu hiperbolą (przybliżenie polega na zaniedbaniu oddziaływania innych ciał niebieskich na sondę). Planeta znajduje się w ognisku hiperboli, a kąt pomiędzy asymptotami jest związany z tym, jak blisko planety przeleci sonda (Rys. 1) – im bliżej, tym większemu odchyleniu ulegnie kierunek jej ruchu. W układzie odniesienia, w którym planeta spoczywa, ruch sondy jest symetryczny względem odwrócenia w czasie, a długość wektora prędkości przy ustalonej odległości od planety jest taka sama w fazie zbliżania, jak w fazie oddalania się sondy od planety. Sonda nadlatuje z daleka mając pewną energię kinetyczną, okrąża planetę i oddala się zachowując tę samą energię, którą miała przed zbliżeniem, istotnej zmianie ulega jedynie kierunek jej ruchu (Rys. 2). Proces ten można porównać do sprężystego odbicia piłeczki od nieruchomej ściany. Piłeczka po odbiciu zachowuje energię kinetyczną, zmienia się jedynie kierunek jej prędkości. Można więc wyobrażać sobie zbliżenie sondy do planety jako rodzaj zderzenia sprężystego.
Chcieliśmy jednak umożliwić naszej sondzie ucieczkę spod jurysdykcji
Słońca. Zastanówmy się zatem, jak to sprężyste zderzenie wygląda w układzie
odniesienia związanym ze Słońcem. W tym układzie planeta się porusza i to
dosyć szybko. Na przykład, prędkość Ziemi w jej ruchu orbitalnym wynosi
około
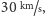 Jowisza około
Jowisza około
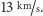 Ponieważ czas przelotu sondy
w porównaniu z okresem orbitalnym planety jest bardzo mały, możemy
w dobrym przybliżeniu przyjąć, że planeta w rozważanym czasie
porusza się ruchem prostoliniowym. Wtedy transformacja prędkości
z układu spoczynkowego planety do układu Słońca polega na dodaniu do
wszystkich wektorów prędkości wektora prędkości planety względem
Słońca. Rozważmy sytuację, w której sonda obiega Słońce po orbicie
w kierunku przeciwnym do kierunku obiegu planety, czyli rozważane
obiekty początkowo poruszają się z grubsza w przeciwnych kierunkach.
Składowe prędkości sondy prostopadłe do kierunku ruchu planety nie
zmienią się, natomiast ulegną zmianie składowe równoległe – w fazie
zbliżania od wartości składowej równoległej odejmie się prędkość
planety, a w fazie oddalania prędkość planety się do niej doda (Rys. 3).
W konsekwencji, jeżeli porównamy składową równoległą prędkości
sondy przed i po zbliżeniu, to będą się one różniły o podwojoną
wartość prędkości planety. Uzyskamy zatem to, co chcieliśmy – sonda po
zbliżeniu będzie się poruszać szybciej! Ponownie możemy zastosować
analogię do odbijania piłeczki. Przelot w pobliżu nieruchomej planety
porównaliśmy do sprężystego odbijania piłeczki o ścianę. Natomiast
analogią przelotu obok planety poruszającej się jest odbijanie piłeczki
od ruchomego obiektu, np. od czoła poruszającego się pociągu. Jeżeli
rzucilibyśmy piłką z prędkością
Ponieważ czas przelotu sondy
w porównaniu z okresem orbitalnym planety jest bardzo mały, możemy
w dobrym przybliżeniu przyjąć, że planeta w rozważanym czasie
porusza się ruchem prostoliniowym. Wtedy transformacja prędkości
z układu spoczynkowego planety do układu Słońca polega na dodaniu do
wszystkich wektorów prędkości wektora prędkości planety względem
Słońca. Rozważmy sytuację, w której sonda obiega Słońce po orbicie
w kierunku przeciwnym do kierunku obiegu planety, czyli rozważane
obiekty początkowo poruszają się z grubsza w przeciwnych kierunkach.
Składowe prędkości sondy prostopadłe do kierunku ruchu planety nie
zmienią się, natomiast ulegną zmianie składowe równoległe – w fazie
zbliżania od wartości składowej równoległej odejmie się prędkość
planety, a w fazie oddalania prędkość planety się do niej doda (Rys. 3).
W konsekwencji, jeżeli porównamy składową równoległą prędkości
sondy przed i po zbliżeniu, to będą się one różniły o podwojoną
wartość prędkości planety. Uzyskamy zatem to, co chcieliśmy – sonda po
zbliżeniu będzie się poruszać szybciej! Ponownie możemy zastosować
analogię do odbijania piłeczki. Przelot w pobliżu nieruchomej planety
porównaliśmy do sprężystego odbijania piłeczki o ścianę. Natomiast
analogią przelotu obok planety poruszającej się jest odbijanie piłeczki
od ruchomego obiektu, np. od czoła poruszającego się pociągu. Jeżeli
rzucilibyśmy piłką z prędkością
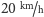 w jadący z prędkością
w jadący z prędkością
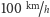 z przeciwka pociąg, to po sprężystym odbiciu piłka leciałaby
z prędkością
z przeciwka pociąg, to po sprężystym odbiciu piłka leciałaby
z prędkością
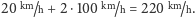 Oczywiście, w układzie
odniesienia związanym z pociągiem prędkości piłki przed i po odbiciu mają
wartość
Oczywiście, w układzie
odniesienia związanym z pociągiem prędkości piłki przed i po odbiciu mają
wartość
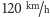 i są przeciwnie skierowane.
i są przeciwnie skierowane.
Dzięki powszechnemu zastosowaniu procy grawitacyjnej udało się przeprowadzić wiele spektakularnych kosmicznych misji, które byłyby niemożliwe do wykonania, gdyby sondy musiały polegać tylko na własnych silnikach. Asysta grawitacyjna może być wykorzystana nie tylko do rozpędzania sond, ale również do ich spowalniania. Wiele szczegółowych informacji na temat wykorzystania tego efektu w konkretnych misjach można znaleźć na stronie NASA i w Wikipedii.
 – prędkość planety względem Słońca,
– prędkość planety względem Słońca,
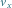 – składowa prędkości sondy
względem Słońca równoległa do prędkości planety,
– składowa prędkości sondy
względem Słońca równoległa do prędkości planety,
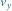 – składowa prędkości sondy
prostopadła do prędkości planety.
– składowa prędkości sondy
prostopadła do prędkości planety.