Konfiguracje Ziemia-Wenus w „boskiej proporcji”
Tak zwana boska proporcja, inaczej złoty podział, to znany od starożytności specjalny sposób podziału odcinka...
Dla odcinka o długości równej 1 stosunek większej części o długości
 do
do
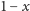 jest równy stosunkowi
jest równy stosunkowi
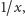
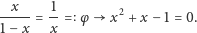
Dodatni pierwiastek tego równania to
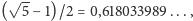 stąd
stąd
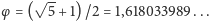 Oznacza to, że część o długości
Oznacza to, że część o długości
 stanowi około
stanowi około
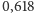 z długości całego odcinka (jak również,
część o długości
z długości całego odcinka (jak również,
część o długości
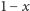 to około
to około
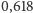 długości
długości
 ).
Walory złotego podziału docenia się od dawna w sztuce: rzeźbie, malarstwie
i architekturze, ponieważ tworzy on miłe dla oka wrażenie harmonii pomiędzy
elementami całości budynku, rzeźby lub obrazu. Złoty podział jest
wszechobecny w przyrodzie: w rozmieszczeniu gałązek i liści wielu roślin,
kształcie muszli itd. Postać wyprostowanego człowieka również dzieli się na
części według złotej proporcji. W matematyce
).
Walory złotego podziału docenia się od dawna w sztuce: rzeźbie, malarstwie
i architekturze, ponieważ tworzy on miłe dla oka wrażenie harmonii pomiędzy
elementami całości budynku, rzeźby lub obrazu. Złoty podział jest
wszechobecny w przyrodzie: w rozmieszczeniu gałązek i liści wielu roślin,
kształcie muszli itd. Postać wyprostowanego człowieka również dzieli się na
części według złotej proporcji. W matematyce
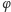 pojawia się w figurach
foremnych: pięciokącie, dziesięciokącie, dwunastościanie i dwudziestościanie,
a także spirali logarytmicznej, w ciągu Fibonacciego i innych obiektach
matematycznych.
pojawia się w figurach
foremnych: pięciokącie, dziesięciokącie, dwunastościanie i dwudziestościanie,
a także spirali logarytmicznej, w ciągu Fibonacciego i innych obiektach
matematycznych.
Zajmiemy się teraz analizą ruchów Ziemi i Wenus w heliocentrycznym
układzie odniesienia. Wyniki będą przybliżone, ponieważ zakładamy, że
orbity planet są okręgami i leżą w jednej płaszczyźnie. Przyjmijmy,
że średnia odległość Wenus–Słońce wynosi
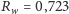 AU
(jednostki astronomicznej, czyli średniej odległości Ziemia–Słońce,
AU
(jednostki astronomicznej, czyli średniej odległości Ziemia–Słońce,
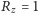 AU). Z trzeciego prawa Keplera w postaci uogólnionej,
AU). Z trzeciego prawa Keplera w postaci uogólnionej,
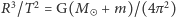 dostajemy, przy założeniu równości
mas planet oraz
dostajemy, przy założeniu równości
mas planet oraz
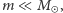 stosunek ich okresów orbitalnych
stosunek ich okresów orbitalnych
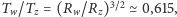 czyli wartość bliską
czyli wartość bliską
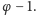 Konfiguracje
pojawiające się w tym układzie odzwierciedlają więc przybliżony złoty podział –
w tym przypadku związaną z częstością ruchu planet „muzyczną harmonię”.
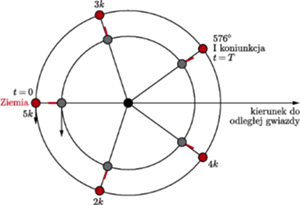
Jeśli zaś chodzi o odległości geometryczne, rysunek 1 przedstawia Wenus
w koniunkcji dolnej. Na powierzchni Wenus zaznaczona jest fikcyjna wieżyczka
skierowana w tym momencie ku Ziemi. Następna koniunkcja Wenus nastąpi po
czasie
Konfiguracje
pojawiające się w tym układzie odzwierciedlają więc przybliżony złoty podział –
w tym przypadku związaną z częstością ruchu planet „muzyczną harmonię”.
Jeśli zaś chodzi o odległości geometryczne, rysunek 1 przedstawia Wenus
w koniunkcji dolnej. Na powierzchni Wenus zaznaczona jest fikcyjna wieżyczka
skierowana w tym momencie ku Ziemi. Następna koniunkcja Wenus nastąpi po
czasie
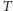 zwanym okresem synodycznym Wenus. Do obliczenia tego
okresu przyjmijmy wyliczone powyżej wartości:
zwanym okresem synodycznym Wenus. Do obliczenia tego
okresu przyjmijmy wyliczone powyżej wartości:
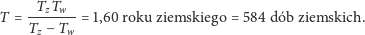
W tym okresie promienie wodzące planet zakreślą kąty: dla Ziemi
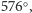 a dla Wenus
a dla Wenus
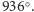 Wenus znajdzie się w koniunkcji
dolnej oznaczonej I. Kolejne koniunkcje dolne zaznaczone są na rysunku 1
w regularnych odstępach. Piąta koniunkcja jest powtórzeniem konfiguracji
początkowej. Czas
Wenus znajdzie się w koniunkcji
dolnej oznaczonej I. Kolejne koniunkcje dolne zaznaczone są na rysunku 1
w regularnych odstępach. Piąta koniunkcja jest powtórzeniem konfiguracji
początkowej. Czas
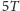 jest okresem powtarzalności konfiguracji tych
trzech ciał w przestrzeni. W czasie
jest okresem powtarzalności konfiguracji tych
trzech ciał w przestrzeni. W czasie
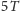 Ziemia wykonuje wokół Słońca
8 pełnych obiegów, a Wenus 13. Rotacja Wenus wokół własnej osi odbywa się
w kierunku wstecznym niż rotacja większości planet i wynosi około 243 dób
ziemskich. Oznacza to, że w ciągu jednego dnia ziemskiego Wenus obraca się
o kąt
Ziemia wykonuje wokół Słońca
8 pełnych obiegów, a Wenus 13. Rotacja Wenus wokół własnej osi odbywa się
w kierunku wstecznym niż rotacja większości planet i wynosi około 243 dób
ziemskich. Oznacza to, że w ciągu jednego dnia ziemskiego Wenus obraca się
o kąt
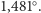 Po pierwszym okresie
Po pierwszym okresie
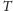 kąt, o jaki obróciła się
Wenus, wynosi więc
kąt, o jaki obróciła się
Wenus, wynosi więc
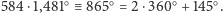
Przy każdej koniunkcji dolnej Wenus zwrócona jest do Ziemi tym samym
miejscem na jej powierzchni (wieżyczką ku Ziemi). Z powodu bardzo
powolnej rotacji doba na Wenus, tzn. odstęp czasu pomiędzy kolejnymi
wschodami Słońca, wynosi
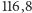 dób ziemskich. Wynika stąd, że
pomiędzy koniunkcjami upływa
dób ziemskich. Wynika stąd, że
pomiędzy koniunkcjami upływa
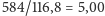 dób wenusjańskich.
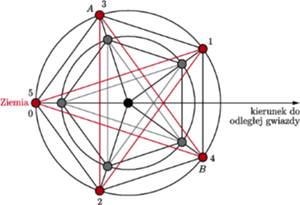
Miejsca koniunkcji Wenus na jej orbicie znajdują się w wierzchołkach
pięciokąta foremnego (Rys. 2). Łącząc odcinkami kolejne pozycje planety
podczas koniunkcji, otrzymujemy dla czasu
dób wenusjańskich.
Miejsca koniunkcji Wenus na jej orbicie znajdują się w wierzchołkach
pięciokąta foremnego (Rys. 2). Łącząc odcinkami kolejne pozycje planety
podczas koniunkcji, otrzymujemy dla czasu
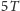 pentagramy: jeden
dotyczący ruchu Ziemi, a drugi Wenus. Punkty przecięcia przekątnych
pięciokąta wyznacza ich złoty podział:
pentagramy: jeden
dotyczący ruchu Ziemi, a drugi Wenus. Punkty przecięcia przekątnych
pięciokąta wyznacza ich złoty podział:
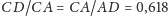 oraz
oraz
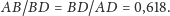 Odkryliśmy więc kolejną harmonię w ruchach
Ziemi i Wenus wokół Słońca. „Boska proporcja” przejawia się w okresach
obiegu tych planet
Odkryliśmy więc kolejną harmonię w ruchach
Ziemi i Wenus wokół Słońca. „Boska proporcja” przejawia się w okresach
obiegu tych planet
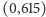 oraz w geometrii dotyczącej koniunkcji Wenus
oraz w geometrii dotyczącej koniunkcji Wenus
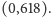 Na rysunku 3 przedstawiony jest dodatkowo ziemski pentagram
z rysunku 2 Jego przecinające się ramiona tworzą w środkowej części
pięciokąt foremny. Okrąg opisany na nim ma promień niemalże równy
średniej odległości Merkurego od Słońca. W rzeczywistości półosie
eliptycznej orbity Merkurego wyraźnie odbiegają od średniej odległości,
podobnie jest w przypadku Plutona (mimośrody ich orbit mają wartości
ponad
Na rysunku 3 przedstawiony jest dodatkowo ziemski pentagram
z rysunku 2 Jego przecinające się ramiona tworzą w środkowej części
pięciokąt foremny. Okrąg opisany na nim ma promień niemalże równy
średniej odległości Merkurego od Słońca. W rzeczywistości półosie
eliptycznej orbity Merkurego wyraźnie odbiegają od średniej odległości,
podobnie jest w przypadku Plutona (mimośrody ich orbit mają wartości
ponad
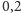 ).
).
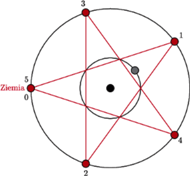
Rys. 3
Wiara w istnienie porządku w rozmieszczeniu i ruchach planet jest dla wielu
uczonych inspiracją do ich poszukiwań. W XVII w. Johannes Kepler
sformułował prawa dotyczące ruchu planet, a XVIII-wieczny astronom Johann
Titius z Wittenbergi podał matematyczną regułę, według której rozmieszczone
miały być planety. Wkrótce później regułę tę rozpowszechnił Johann
Bode. Reguła Titiusa–Bodego umożliwia w prosty sposób obliczenie
przybliżonych średnich odległości planet od Słońca. Odległość ta to
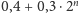 AU, gdzie
AU, gdzie
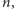 począwszy od Merkurego, wynosi
począwszy od Merkurego, wynosi
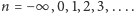 Mimo zaskakująco dobrej zgodności dla
większości planet reguła ta nie wynika wprost z równań mechaniki nieba,
może za to być traktowana jako wygodne „pierwsze przybliżenie”.
Mimo zaskakująco dobrej zgodności dla
większości planet reguła ta nie wynika wprost z równań mechaniki nieba,
może za to być traktowana jako wygodne „pierwsze przybliżenie”.
Przedstawione wyżej obliczenia traktuję jako ciekawostkę, która daje mi poczucie, że ruchami ciał niebieskich rządzą prawa o walorach estetycznych (muzyka sfer?). Przyczyną tych prawidłowości są, jak obecnie wiemy, wzajemne oddziaływania w układzie Słońce–najbliższe planety, w szczególności występowania rezonansów pomiędzy składnikami układu. Dlaczego pojawił się tu złoty podział? Tego nie wiem, zachęcam jednak do własnych badań w poszukiwaniu nowych prawidłowości.