Rys. 1 Dzienny ruch Słońca wokół osi ziemskiej i cień rzucany przez pręt ustawiony wzdłuż tej osi.

Rys. 2 Dzienny ruch cienia pręta-wskazówki zegara słonecznego (w lecie – Słońce powyżej płaszczyzny równika).

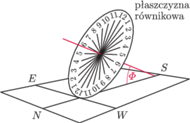
Rys. 3 Ustawienie zegara równikowego

Ruch dobowy Słońca

Jak wiemy od czasów Kopernika, Ziemia wiruje wokół własnej osi, wykonując jeden obrót na dobę. Załóżmy, że stwierdzenie to jest prawdziwe w układzie odniesienia związanym ze Słońcem, co odpowiada rozumieniu doby jako doby słonecznej. Wobec tego w naszym, ziemskim układzie odniesienia ruch Słońca odbywa się wokół osi ziemskiej, jak na rysunku 1. Na rysunku tym nie ma Ziemi, za to umieszczono wzdłuż osi ziemskiej pręt. Ten pręt jest typowym elementem zegara słonecznego, a jego cień stanowi wskazówkę tego zegara, która krąży dookoła pręta, wykonując pełny obrót w ciągu doby. (W praktyce dogodniej nazywać wskazówką sam pręt, a nie jego cień, i taką konwencję odtąd przyjmujemy.) Na płaszczyźnie prostopadłej do osi ziemskiej można więc narysować okrąg, a na nim w równych odstępach zaznaczyć kolejne godziny, które będzie wskazywał cień. Oczywiście, o godzinie 12 cień będzie wskazywał południe. Wszystko to przedstawia rysunek 2.

W ten sposób otrzymaliśmy najprostszą wersję zegara słonecznego, czyli

Zegar równikowy

Jego konstrukcja jest prosta, ale ma jedną wadę: płaszczyzna równikowa nie jest pozioma, chyba że umieścimy nasz zegar na biegunie. Jeżeli jednak chcemy wykorzystać ten zegar w Polsce, musimy pochylić jego oś w stronę północy (Rys. 3), tak żeby tworzyła z płaszczyzną poziomą kąt równy szerokości geograficznej, która, na przykład, w Warszawie wynosi 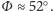 Wtedy oś zegara będzie równoległa do osi ziemskiej.

Na rysunkach 1 i 2 Słońce znajduje się na pewnej wysokości (kątowej) nad płaszczyzną równika. Jaka jest ta wysokość w rzeczywistości i od czego zależy? Żeby odpowiedzieć na to pytanie, musimy przyjrzeć się dokładniej względnemu ruchowi Słońca i Ziemi.

Roczny ruch Ziemi wokół Słońca

Tym razem wróćmy do układu odniesienia wybranego przez Kopernika i zobaczmy na rysunku 4, jak wygląda ruch Ziemi po jej orbicie, którą w przybliżeniu uznamy za okrąg (całkiem spory, o promieniu około 150 milionów kilometrów).

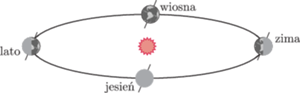
Rys. 4 Ruch Ziemi po orbicie wokół Słońca.

Widać, że Słońce raz znajduje się powyżej (od strony północy), a raz poniżej (od południa) płaszczyzny równika. Maksymalny kąt, jaki promienie słoneczne tworzą z płaszczyzną równika, jest kątem nachylenia  płaszczyzny równika do płaszczyzny orbity ziemskiej, i wynosi około 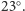 Kąt ten jest równy szerokości geograficznej zwrotników, które, jak wiadomo, ograniczają obszar wokół równika, w którym Słońce może pojawić się w zenicie. To wszystko można wyczytać z rysunku 4. Wróćmy na chwilę do rysunku 2. Widać na nim, że cień górnego końca wskazówki zakreśla powierzchnię (boczną) stożka. W świetle powyższych wyjaśnień łatwo zauważyć, że tworząca tego stożka jest ustawiona do płaszczyzny równikowej pod kątem, który zmienia się w ciągu roku miedzy 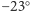 a 

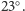
Rys. 5 Stożek cienia dolnego końca wskazówki w dniu przesilenia zimowego. Linia przerywana – miesiąc wcześniej lub później.

Pozostawiam Czytelnikowi wykazanie, że promień 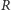 okręgu reprezentującego dzień, w którym Ziemia zakreśliła w swoim ruchu rocznym dookoła Słońca (liczonym od przesilenia zimowego lub letniego) kąt 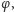 jest powiązany z (liczoną od płaszczyzny tarczy) długością 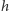 wskazówki zależnością

(*)

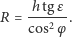Fakt ten możemy wykorzystać do narysowania na tarczy zegara okręgów reprezentujących różne daty (patrz okładka), z wyjątkiem, oczywiście, dni równonocy, kiedy Słońce znajduje się w płaszczyźnie równika, a więc stożek redukuje się do płaszczyzny.

Rys. 6 Zegar równikowy (użyteczny tylko w lecie), wykonany przez firmę Neolit.

W praktyce jednak najczęściej się tego nie robi, ponieważ skończony promień tarczy zegara wyklucza pewne zakresy dat wokół dni równonocy. Widać także, że zegar równikowy z nieprzezroczystą tarczą, na której skala jest naniesiona tylko z jednej strony (Rys. 6), jest użyteczny tylko przez pół roku, kiedy Słońce znajduje się po odpowiedniej stronie tarczy.

Rozwiązaniem, które nie ma tej wady, jest zastąpienie tarczy pierścieniem, na którego wewnętrznej powierzchni naniesiono skalę godzinową.

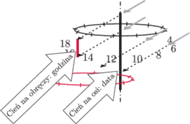
Rys. 7 Idea zegara równikowego z dwiema skalami: godzina na pierścieniu i data na pręcie.

Przy okazji można teraz wrócić do idei połączenia zegara z kalendarzem. Jeżeli pierścień jest pełny, to będzie on rzucał cień na wskazówkę, i to w miejscu określonym przez wysokość Słońca nad płaszczyzną równikową, która, jak wiemy, zmienia się w cyklu rocznym. Możemy więc zaznaczyć na pręcie wskazówki skalę dat (dzień i miesiąc), co schematycznie przedstawia rysunek 7.

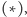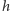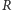Skala dat takiego zegara nie jest wprawdzie jednoznaczna (każdemu położeniu cienia pierścienia na pręcie – poza skrajnymi – odpowiadają dwie daty w roku), ale jest to problem każdego zegara słonecznego i musimy się z nim pogodzić. Aby wyskalować kalendarz, możemy posłużyć się wzorem  w którym  ma tym razem znaczenie wysokości znaku daty na skali przy ustalonym promieniu  pierścienia i jest dodatnie latem, a ujemne zimą.

Inne typy zegarów słonecznych

Zegar równikowy nie jest bynajmniej najpopularniejszym zegarem słonecznym. Znacznie wygodniej jest posługiwać się skalą nie ukośną, ale poziomą lub pionową. Inaczej mówiąc, będziemy musieli stożek z rysunku 2 przeciąć płaszczyzną poziomą lub pionową, a więc w stosunku do osi stożka (równoległej do osi ziemskiej) ukośną. Płaszczyzny określone przez cień wskazówki przetną się z taką skalą wzdłuż prostych, a więc linie reprezentujące kolejne godziny będą nadal proste (choć nie będą już równomiernie rozmieszczone). Jednak linie reprezentujące różne daty nie będą teraz, jak dla zegara równikowego, okręgami, ale jako wynik przecięcia powierzchni stożka ukośną płaszczyzną będą miały kształt hiperbol. Wykreślenie tych hiperbol (znów okładka) nie jest już tak proste, jak narysowanie okręgów o wyliczonych promieniach, proponuję więc skorzystać w tym celu z oprogramowania dostępnego w Internecie, na przykład zaglądając na stronę http://www.sundials.co.uk/comprogs.htm

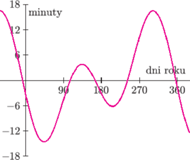
Rys. 8 Wykres równania czasu – poprawki, którą należy odjąć od odczytu zegara słonecznego.

Jak dokładny jest zegar słoneczny?

Oprócz oczywistych czynników wpływających na dokładność takiego zegara, jak staranność wykonania i ustawienia, czy nieostrość cienia, warto zwrócić uwagę na dwa źródła błędu systematycznego. Pierwsze z nich to różnica między czasem oficjalnym, ustalanym administracyjnie dla określonego obszaru geograficznego, a czasem lokalnym, zmieniającym się z długością geograficzną. Tę różnicę najłatwiej uwzględnić dla zegara równikowego, obracając jego tarczę wokół osi wskazówki o odpowiedni kąt, który można wyznaczyć empirycznie przez porównanie z zegarem wskazującym czas oficjalny. Dla zegara pionowego lub poziomego należy wprowadzić odpowiednią poprawkę (cztery minuty na stopień długości geograficznej) do programu obliczającego skalę. Drugim źródłem błędu systematycznego są przybliżenia, które przyjęliśmy, rozpoczynając nasze rozważania. A więc przede wszystkim kołowy kształt orbity ziemskiej. W rzeczywistości ma ona kształt spłaszczonej elipsy. Z tego powodu prędkość kątowa Ziemi na orbicie zmienia się w czasie zgodnie z prawem zachowania pędu: jest największa, gdy Ziemia jest najbliżej Słońca. Prędkości kątowe ruchu orbitalnego i wirowego Ziemi dodają się, i to wektorowo, ponieważ odbywają się wokół różnych osi. Z tego powodu „czas” odmierzany przez zegar słoneczny nie biegnie równomiernie, ale czasem szybciej, czasem wolniej, zależnie od pory roku. Wynikająca stąd niedokładność zegara słonecznego jest całkiem spora – może dochodzić do kwadransa. Poprawka, którą należy uwzględnić, aby od odczytu zegara słonecznego przejść do dokładnego czasu, jest określona przez tzw. równanie czasu, które w formie wykresu (Rys. 8) umieszcza się czasem dla wygody na samym zegarze słonecznym.