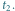Jak wyznaczyć odległość Ziemia–Księżyc?
Odpowiedź na zawarte w tytule pytanie brzmi: bardzo łatwo. Wystarczy lornetka, a w szczególnych sytuacjach można nawet prowadzić obserwacje gołym okiem. Ta ostatnia metoda umożliwia, oczywiście, jedynie zgrubne oszacowanie odległości, natomiast rezultaty obserwacji wykonanych lornetką zasługują już na miano pomiaru.
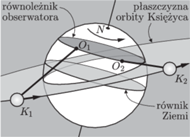
Rys. 1 Położenia obserwatora
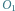 i
i
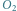 oraz Księżyca
oraz Księżyca
 i
i
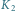 w chwilach
obserwacji, odpowiednio,
w chwilach
obserwacji, odpowiednio,
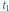 i
i
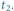
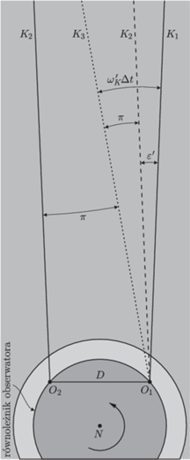
Rys. 2 Rzuty kierunków do Księżyca na płaszczyznę ruchu obserwatora, czyli na płaszczyznę równoleżnika.
Nawet jeśli, Drogi Czytelniku, nie jesteś jeszcze astronomem amatorem, podana wyżej odpowiedź jest słuszna także i w Twoim przypadku. Kolorowym tekstem podamy tu kilka rad dla bardzo początkujących adeptów sztuki obserwacji nieba.
Kilkakrotne spojrzenie na niebo w odstępie paru godzin przekonuje nas,
że Księżyc nieustannie zmienia swoje położenie względem gwiazd,
przemieszczając się na ich tle w lewo, tj. przeciwnie do kierunku swojego ruchu
względem horyzontu. Ruch ten jest złożeniem ruchu orbitalnego Księżyca oraz
ruchu obserwatora poruszającego się w przestrzeni wraz z obracającą się Ziemią.
Jeżeli zatem z zaobserwowanego kątowego przemieszczenia Księżyca
 wyodrębnimy tę jego część
wyodrębnimy tę jego część
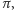 która jest następstwem zmiany
miejsca obserwacji, będziemy mogli wyznaczyć odległość do Księżyca
która jest następstwem zmiany
miejsca obserwacji, będziemy mogli wyznaczyć odległość do Księżyca
 na podstawie odległości
na podstawie odległości
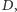 o jaką przesunął się podczas
pomiarów obserwator.
o jaką przesunął się podczas
pomiarów obserwator.
Jak wyznaczyć wartość
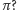 Przyjmijmy, że obserwator
dokonał dwukrotnej rejestracji pozycji Księżyca na tle gwiazd.
Rysunek 1 przedstawia położenia obserwatora
Przyjmijmy, że obserwator
dokonał dwukrotnej rejestracji pozycji Księżyca na tle gwiazd.
Rysunek 1 przedstawia położenia obserwatora
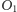 i
i
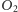 oraz
Księżyca
oraz
Księżyca
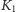 i
i
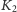 w momencie pierwszej i drugiej
obserwacji, odpowiednio
w momencie pierwszej i drugiej
obserwacji, odpowiednio
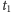 i
i
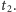 Na rysunku 2 ta sama
sytuacja jest pokazana od strony północnego bieguna Ziemi. Na tym
rysunku położenia obserwatora oraz kierunki obserwator Księżyc są
zrzutowane na płaszczyznę, w której porusza się obserwator, tj. na płaszczyznę
równoleżnika obserwatora. Dla uproszczenia rysunku przyjęto, że
obserwacje wykonane zostały w chwilach
Na rysunku 2 ta sama
sytuacja jest pokazana od strony północnego bieguna Ziemi. Na tym
rysunku położenia obserwatora oraz kierunki obserwator Księżyc są
zrzutowane na płaszczyznę, w której porusza się obserwator, tj. na płaszczyznę
równoleżnika obserwatora. Dla uproszczenia rysunku przyjęto, że
obserwacje wykonane zostały w chwilach
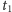 i
i
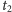 symetrycznych
względem chwili
symetrycznych
względem chwili
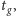 w której Księżyc osiąga największą wysokość
ponad horyzontem
w której Księżyc osiąga największą wysokość
ponad horyzontem
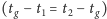 . Wówczas przemieszczenie
. Wówczas przemieszczenie
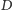 obserwatora między pierwszą i drugą obserwacją będzie prostopadłe
do kierunku na Księżyc w chwili jego górowania. Ze względu na znikomość
tego przemieszczenia w porównaniu z odległością do gwiazd można
przyjąć, że dwie równoległe linie oznaczone (na Rys. 2) symbolem
obserwatora między pierwszą i drugą obserwacją będzie prostopadłe
do kierunku na Księżyc w chwili jego górowania. Ze względu na znikomość
tego przemieszczenia w porównaniu z odległością do gwiazd można
przyjąć, że dwie równoległe linie oznaczone (na Rys. 2) symbolem
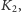 wychodzące z miejsc obserwacji
wychodzące z miejsc obserwacji
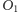 i
i
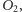 wskazują na
tle gwiazd ten sam punkt. Jest to miejsce, w którym jest widoczny Księżyc
podczas drugiej obserwacji. Prosta
wskazują na
tle gwiazd ten sam punkt. Jest to miejsce, w którym jest widoczny Księżyc
podczas drugiej obserwacji. Prosta
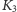 (linia kropkowana) pokazuje
natomiast kierunek do Księżyca, jaki wskazałby obserwator w chwili
(linia kropkowana) pokazuje
natomiast kierunek do Księżyca, jaki wskazałby obserwator w chwili
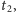 gdyby patrzył z miejsca, w którym dokonywał pierwszej
obserwacji, czyli w przypadku, gdyby przemieszczenie Księżyca na tle gwiazd
powodowane było jedynie jego ruchem orbitalnym. Z rysunku 2 wynika także
związek między przemieszczeniem
gdyby patrzył z miejsca, w którym dokonywał pierwszej
obserwacji, czyli w przypadku, gdyby przemieszczenie Księżyca na tle gwiazd
powodowane było jedynie jego ruchem orbitalnym. Z rysunku 2 wynika także
związek między przemieszczeniem
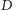 i odległością do Księżyca
i odległością do Księżyca
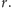 Z uwagi na to, że kąt
Z uwagi na to, że kąt
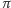 jest bardzo mały, spełniają one
zależność
jest bardzo mały, spełniają one
zależność
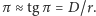
Górowanie jest chwilą, w której obiekt osiąga największą wysokość ponad horyzontem, czyli wtedy, gdy przechodzi on przez płaszczyznę prostopadłą do horyzontu, przecinającą go wzdłuż kierunku północ-południe. Wystarczającą dokładność wyznaczenia
można uzyskać, wykonując obserwacje gołym okiem. Wystarczy, na przykład, określić chwile
i
ograniczające przedział czasu, w którym będzie się wydawało, że Księżyc znajduje się w kierunku południowym. Wartości te pozwolą oszacować zarówno moment górowania
jak i niepewność oszacowania
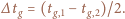
Rysunek 3 przedstawia położenia Księżyca na tle gwiazd tak, jak widzi je
ziemski obserwator. Zaznaczono tam również przestrzenną orientację
płaszczyzny równoległej do płaszczyzny ruchu obserwatora. Zaobserwowane
przemieszczenie Księżyca względem gwiazd
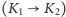 o kąt
o kąt
 jest wypadkową orbitalnego przemieszczenia Księżyca o kąt
jest wypadkową orbitalnego przemieszczenia Księżyca o kąt
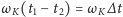 w płaszczyźnie orbity Księżyca
w płaszczyźnie orbity Księżyca
 oraz
przemieszczenia o kąt
oraz
przemieszczenia o kąt
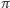 wynikający z przesunięcia obserwatora
w płaszczyźnie równoległej do płaszczyzny jego ruchu
wynikający z przesunięcia obserwatora
w płaszczyźnie równoległej do płaszczyzny jego ruchu
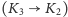 .
Zwrot przemieszczenia
.
Zwrot przemieszczenia
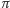 jest przeciwny do kierunku ruchu obserwatora,
czyli zgodny z ruchem gwiazd względem horyzontu – w prawo.
jest przeciwny do kierunku ruchu obserwatora,
czyli zgodny z ruchem gwiazd względem horyzontu – w prawo.
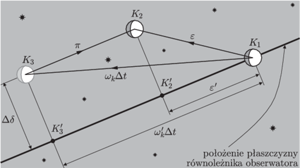
Rys. 3 Położenia Księżyca
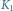 i
i
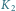 na tle gwiazd obserwowane z Ziemi w chwilach
na tle gwiazd obserwowane z Ziemi w chwilach
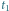 i
i
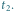 Przez
Przez
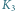 oznaczono położenie Księżyca, jakie widziałby
nieruchomy obserwator pozostający stale w
oznaczono położenie Księżyca, jakie widziałby
nieruchomy obserwator pozostający stale w
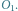 Punkty
Punkty
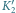 i
i
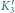 są rzutami
punktów odpowiednio
są rzutami
punktów odpowiednio
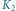 i
i
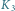 na płaszczyznę równoleżnika obserwatora.
na płaszczyznę równoleżnika obserwatora.
Najprostszy sposób wyznaczenia
polega na zarejestrowaniu pozycji Księżyca względem gwiazd w chwilach jego górowania
i
podczas dwóch kolejnych nocy (rys. a). W chwili górowania pozycja obserwatora względem prostej łączącej środek Ziemi i Księżyca jest taka sama, więc zaobserwowane kątowe przemieszczenie Księżyca
będzie spowodowane wyłącznie jego ruchem orbitalnym.Oznacza to, że
Jeśli przemieszczenie Księżyca na tle gwiazd
będzie określane na oko, to usprawiedliwione będzie przyjmowanie na
wartości średniej wynikającej z okresu jego obiegu wokół Ziemi
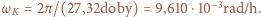
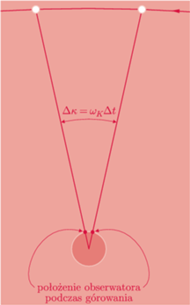
Rys. a Wyznaczanie chwilowej prędkości kątowej Księżyca.
Punkty
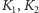 i
i
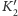 oraz
oraz
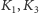 i
i
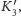 przedstawione
na rysunku 3, wyznaczają dwa trójkąty sferyczne. Długości boków tych
trójkątów można opisać kątami odpowiednio
przedstawione
na rysunku 3, wyznaczają dwa trójkąty sferyczne. Długości boków tych
trójkątów można opisać kątami odpowiednio
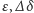 i
i
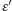 oraz
oraz
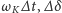 i
i
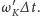 Jeśli odstęp czasu pomiędzy pierwszą i drugą
obserwacją
Jeśli odstęp czasu pomiędzy pierwszą i drugą
obserwacją
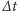 będzie wynosił kilka godzin, to wszystkie te kąty będą
bardzo małe i trójkąty sferyczne
będzie wynosił kilka godzin, to wszystkie te kąty będą
bardzo małe i trójkąty sferyczne
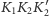 i
i
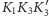 można
przybliżyć przez trójkąty płaskie. Otrzymamy stąd:
można
przybliżyć przez trójkąty płaskie. Otrzymamy stąd:
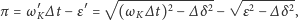 | (1) |
co pozwoli nam już obliczyć odległość do Księżyca
 przy
znajomości przesunięcia
przy
znajomości przesunięcia
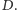
Do wyznaczenia wartości kąta
niezbędna jest znajomość kierunku, w którym przesunął się Księżyc względem gwiazd w wyniku ruchu obserwatora
. Z powodu rotacji Ziemi każdy obserwator porusza się po okręgu (równoleżniku), którego płaszczyzna jest prostopadła do osi obrotu Ziemi. Jeśli obserwowany obiekt znajduje się w kierunku tworzącym z osią obrotu Ziemi kąt przekraczający
jak ma to miejsce w przypadku Księżyca, to w kilkugodzinnym okresie obserwacji, obejmującym moment górowania, przemieszczenie obiektu spowodowane ruchem obserwatora będzie niemal dokładnie równoległe do płaszczyzny ruchu obserwatora. Ponieważ oś obrotu Ziemi można utożsamiać z osią obrotu nieba, więc płaszczyzna ruchu obserwatora (płaszczyzna równoleżnika) jest prostopadła do tej osi. Na rysunku lub mapie nieba reprezentowała ją będzie linia przechodząca przez miejsce, w którym znajduje się Księżyc i prostopadła do kierunku na biegun nieba (Gwiazdę Polarną) lub linia równoległa do kierunku dobowego ruchu gwiazd. Zwrot przesunięcia Księżyca spowodowany ruchem obserwatora będzie przeciwny do ruchu obserwatora, czyli zgodny z kierunkiem dobowego ruchu gwiazd.
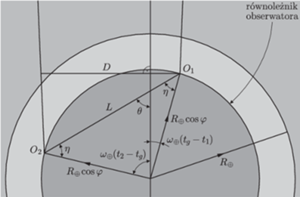
Rys. 4 Widok Ziemi od strony bieguna. Przez
 i
i
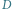 oznaczono przemieszczenie
obserwatora oraz rzut tego przemieszczenia na kierunek prostopadły do kierunku Ziemia–Księżyc
w chwili górowania Księżyca. Jak poprzednio,
oznaczono przemieszczenie
obserwatora oraz rzut tego przemieszczenia na kierunek prostopadły do kierunku Ziemia–Księżyc
w chwili górowania Księżyca. Jak poprzednio,
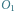 i
i
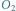 oznaczają położenia
obserwatora w chwilach odpowiednio
oznaczają położenia
obserwatora w chwilach odpowiednio
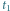 i
i
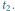
Wyznaczając przesunięcie
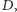 warto uwzględnić sytuację ogólniejszą od
przedstawionej na rysunku 2, mianowicie taką, że przestrzenne przesunięcie
obserwatora
warto uwzględnić sytuację ogólniejszą od
przedstawionej na rysunku 2, mianowicie taką, że przestrzenne przesunięcie
obserwatora
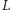 nie jest prostopadłe do kierunku na Księżyc w chwili
jego górowania, tj. gdy
nie jest prostopadłe do kierunku na Księżyc w chwili
jego górowania, tj. gdy
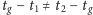 (Rys. 4). Patrząc na
trójkąt o wierzchołkach w punktach
(Rys. 4). Patrząc na
trójkąt o wierzchołkach w punktach
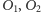 i w środku Ziemi,
stwierdzamy, że
i w środku Ziemi,
stwierdzamy, że
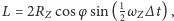 gdzie
gdzie
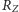 jest
promieniem Ziemi,
jest
promieniem Ziemi,
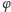 szerokością geograficzną obserwatora,
zaś
szerokością geograficzną obserwatora,
zaś
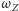 prędkością kątową ruchu wirowego Ziemi. Rzut
całkowitego przestrzennego przemieszczenia obserwatora
prędkością kątową ruchu wirowego Ziemi. Rzut
całkowitego przestrzennego przemieszczenia obserwatora
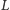 na
kierunek prostopadły do kierunku Ziemia–Księżyc w chwili górowania
Księżyca jest równy
na
kierunek prostopadły do kierunku Ziemia–Księżyc w chwili górowania
Księżyca jest równy
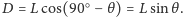 Ponieważ zaś
Ponieważ zaś
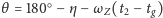 oraz
oraz
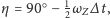 więc ostatecznie
otrzymamy
więc ostatecznie
otrzymamy
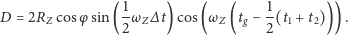 | (2) |
Podstawiając obliczone ze wzorów (1) i (2) wielkości
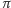 oraz
oraz
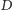 do zależności
do zależności
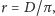 uzyskujemy szukaną odległość do
Księżyca.
uzyskujemy szukaną odległość do
Księżyca.
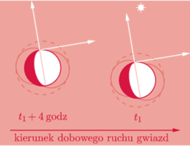
Rys. b Przykład przybliżonej oceny położenia Księżyca w oparciu o jeden bliski, jasny obiekt. Linią przerywaną narysowane są okręgi informujące o wielkości błędu lokalizacji tarczy Księżyca.
Względna dokładność wyznaczenia kątów
i
będzie tym większa, im dłuższy będzie odstęp czasu
między obserwacjami. Wzrostowi dokładności sprzyjała będzie również sytuacja, gdy Księżyc będzie położony w pobliżu jasnych gwiazd lub planet. Minimalnym wymogiem byłby jeden jasny obiekt w odległości nieprzekraczającej średnicy pola widzenia lornetki. W tym przypadku do zbudowania układu odniesienia pozwalającego ocenić przesunięcie Księżyca względem obiektu należy wykorzystać dwa dowolne punkty na tarczy Księżyca lub przynajmniej jego rogi (Rys. b). Rezultatem obserwacji powinno być zaznaczenie na rysunku lub mapie dwóch położeń Księżyca względem gwiazd, zanotowanie chwil
i
dokonania tych lokalizacji oraz zaznaczenie kierunku ruchu obserwatora.
Jeśli zdarzy się tak, że w pobliżu Księżyca znajdzie się jasna gwiazda lub jedna z jasnych planet (np. Wenus, Mars, Jowisz, Saturn), a okres
nie będzie krótszy niż cztery godziny, to oceny przesunięcia Księżyca będzie można dokonać nawet bez korzystania z lornetki. Sytuację taką należy potraktować jak zaproszenie do naukowej zabawy (jej rezultat będzie bowiem tylko grubym oszacowaniem odległości). Obserwacja polegała będzie na zapamiętaniu położenia Księżyca względem jasnego obiektu w chwili
i porównaniu go z położeniem w chwili
Zaobserwowane w ten sposób przesunięcie kątowe
najlepiej będzie określać jako wielokrotność średnicy Księżyca, a następnie wyrazić je w radianach, przyjmując na średnicę tarczy wartość
Gdy zatem, Drogi Czytelniku, zobaczysz w pobliżu Księżyca jasny obiekt, to – dla ułatwienia pamięciowych rachunków – możesz przyjąć, że kątowa średnica Księżyca jest równa
zaniedbać
oraz pamiętać, że w ciągu godziny Ziemia przenosi każdego europejczyka na odległość około 1000 km. Przy tych założeniach, jeśli
będzie wyrażone w godzinach, a
jako wielokrotność średnic Księżyca, to
zaś
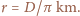
Udanych obserwacji i dobrej zabawy!
 i
i
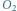 oraz Księżyca
oraz Księżyca
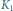 i
i
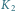 w chwilach
obserwacji, odpowiednio,
w chwilach
obserwacji, odpowiednio,
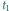 i
i
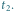
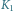 i
i
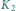 na tle gwiazd obserwowane z Ziemi w chwilach
na tle gwiazd obserwowane z Ziemi w chwilach
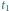 i
i
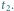 Przez
Przez
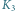 oznaczono położenie Księżyca, jakie widziałby
nieruchomy obserwator pozostający stale w
oznaczono położenie Księżyca, jakie widziałby
nieruchomy obserwator pozostający stale w
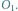 Punkty
Punkty
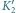 i
i
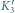 są rzutami
punktów odpowiednio
są rzutami
punktów odpowiednio
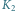 i
i
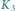 na płaszczyznę równoleżnika obserwatora.
na płaszczyznę równoleżnika obserwatora.
 i
i
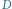 oznaczono przemieszczenie
obserwatora oraz rzut tego przemieszczenia na kierunek prostopadły do kierunku Ziemia–Księżyc
w chwili górowania Księżyca. Jak poprzednio,
oznaczono przemieszczenie
obserwatora oraz rzut tego przemieszczenia na kierunek prostopadły do kierunku Ziemia–Księżyc
w chwili górowania Księżyca. Jak poprzednio,
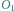 i
i
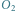 oznaczają położenia
obserwatora w chwilach odpowiednio
oznaczają położenia
obserwatora w chwilach odpowiednio
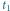 i
i