Co to są radialne prędkości gwiazd

Spektroskopia pozwala również na niemal bezpośredni pomiar radialnej prędkości gwiazdy. Jak sama nazwa wskazuje, prędkość radialna to rzut prędkości gwiazdy (względem obserwatora) na kierunek patrzenia. Zgodnie z przyjętą konwencją, gdy ruch zachodzi w kierunku od obserwatora, prędkość radialna jest uważana za dodatnią. Nietrudno zgadnąć, że nawet gdyby gwiazdy były nieruchome względem Słońca, to sam ruch obrotowy i obiegowy Ziemi wokół Słońca powodowałby, że ich prędkości radialne byłyby niezerowe. Ruch orbitalny Ziemi dawałby bowiem zmiany prędkości radialnych w zakresie 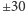 km/s, wirowy zaś jedynie 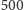 m/s, w zależności od położenia obserwatora na Ziemi.

Do pomiarów prędkości radialnych gwiazd astronomowie wykorzystują znane z fizyki zjawiska: rozszczepienie światła i zjawisko Dopplera. Istotne znaczenie ma także fakt, że Wszechświat składa się z takich samych atomów, które występują na Ziemi, co pozwala nam identyfikować linie w widmach gwiazd. Doppler zauważył, że częstość dźwięku powinna zależeć od prędkości obserwatora i prędkości źródła. W zastosowaniu do fal elektromagnetycznych wzór Dopplera przewiduje, że prędkość względna  źródła światła i obserwatora (wzdłuż kierunku widzenia, czyli prędkość radialna) ma się tak do prędkości światła c jak przesunięcie 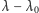 linii widmowej obserwowanej na fali 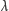 do laboratoryjnej długości fali 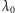 tej linii:

Tak więc, aby zmierzyć prędkość radialną, musimy wpierw otrzymać widmo gwiazdy, zidentyfikować występujące w nim linie, a następnie zmierzyć ich przesunięcia względem położeń laboratoryjnych. Oczywiście, otrzymany wynik należy skorygować uwzględniając ruch wirowy i orbitalny Ziemi. Technika ta jest prosta i stosowana jest z powodzeniem od lat. Kłopoty zaczynają się dopiero, gdy chcemy ją zastosować do pomiaru bardzo małych prędkości, czyli przy bardzo małych przesunięciach linii. Na czym polega problem?

Z jaką dokładnością mierzymy prędkości radialne

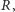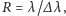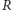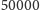Każde widmo gwiazdy charakteryzuje się pewną rozdzielczością, zależną od budowy spektrografu i zastosowanego detektora, na którym widmo jest zapisane. Wielkość ta,  określa, jak odległe są od siebie dwa kolejne odróżnialne elementy widma i jest zdefiniowana jako  czyli jako stosunek długości fali do owej najmniejszej odległości elementów widma. Dobre spektrografy astronomiczne osiągają  od  do 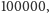 choć buduje się spektrografy o jeszcze większej rozdzielczości. Oczywiście, 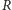 określa również najmniejszą prędkość radialną, jaką można danym spektrografem zmierzyć przy pomiarze położenia jednej linii widmowej. Przy 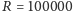 dokładność będzie wynosić 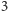 km/s. 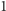Dokładność można poprawić mierząc więcej linii, ale w praktyce nie dostaniemy dokładności lepszej niż około  km/s.

Co stoi na przeszkodzie? Po pierwsze – mechaniczna niestabilność spektrografu. Można ją zminimalizować, stosując spektrograf typu Coude, czyli umieszczony w oddzielnym pomieszczeniu, a nie na teleskopie. Drugim źródłem niedokładności okazał się proces kalibracji widm gwiazdowych. Aby dokonać takiej kalibracji, należy obok widma gwiazdy zarejestrować jakieś dobrze znane widmo, np. lampy Th-Ar. Mierząc położenia  znanych linii na detektorze tworzy się tzw. funkcję dyspersji 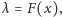 która następnie pozwala określić nieznane długości fal w widmie gwiazdy na podstawie ich położenia na detektorze. Ten właśnie proces okazał się nieść szczególnie wiele niepewności pomiarowych. Przede wszystkim widmo lampy porównania nie przechodziło w teleskopie i w spektrografie tej samej drogi, co światło gwiazdy. Ponadto widmo lampy kalibracyjnej rejestrowane było w nieco innym czasie, niż widmo gwiazdy. Powodowało to, że między tymi dwoma widmami występować mogły nieprzewidywalne przesunięcia, a co więcej, kształt (profil) linii w obu tych widmach był nieco inny, bowiem były one tworzone w faktycznie różnych układach optycznych. Dlatego przełomem w precyzyjnych pomiarach prędkości radialnych okazało się uzyskiwanie widma kalibracyjnego i widma gwiazdy za pomocą tego samego układu optycznego i jednocześnie. Początkowo eksperymentowano z widmem pary wodnej obecnej w atmosferze Ziemi, później zaczęto umieszczać przed teleskopem naczynie ( „komórkę”) zawierające gaz, którego widmo stanowić miało wzorzec do kalibracji. Ostatecznie w wyniku wielu doświadczeń zdecydowano się na komórki z parami jodu I 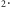  Pary jodu – poza tym, że są silnie trujące – mają też inna wadę: pochłaniają część widma gwiazdy, bowiem komórka faktycznie gra rolę filtru, który w zakresie 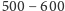 nm ma po kilkadziesiąt linii absorpcyjnych na 1 nm. Rejestrowane widmo gwiazdy zawiera więc dodatkowo tysiące wąskich linii absorpcyjnych, stanowiących wyśmienite widmo kalibracyjne, które ma jeszcze jedną zaletę. Ponieważ światło, na którym swe piętno w postaci linii absorpcyjnych wycisnęły pary jodu, przeszło przez cały układ optyczny, kształt linii widma kalibracyjnego niesie informację o tym, jak układ optyczny ten kształt modyfikuje. Innymi słowy, uzyskawszy widmo par jodu w laboratorium i porównawszy je z widmem uzyskanym danym teleskopem i spektrografem, możemy odtworzyć tzw. profil instrumentalny stosowanego do pomiarów prędkości radialnych układu optycznego.

Wspomniałem już, że stosując tradycyjną metodę pomiaru można polepszyć dokładność mierząc przesunięcia wielu linii. Ilu? Tu odpowiedź jest prosta: najlepiej wszystkich. W tym miejscu pojawia się oczywisty problem techniczny: jak zmierzyć położenia wszystkich linii w widmie, skoro są ich przecież tysiące?! Otóż tych położeń w ogóle się nie mierzy! Najpierw rejestrujemy widmo gwiazdy bez komórki z jodem oraz wykonujemy serię zdjęć widma tej gwiazdy z użyciem komórki (bo chcemy mierzyć zmiany prędkości radialnej). Mając widmo „czyste”, widmo samego jodu oraz profil instrumentalny (wszystko oczywiście w zapisie cyfrowym), każemy teraz komputerowi wymodelować widmo gwiazdy z nałożonym widmem jodu dla rozmaitych przesunięć dopplerowskich. Najważniejsze jest to, że w komputerze przesunięcia te będą bardzo precyzyjnie określone. Któreś widmo modelowe będzie pasować do któregoś widma z serii obserwacyjnej, a komputer wskaże (i to bardzo dokładnie!), jakiemu odpowiada to przesunięciu dopplerowskiemu. Stwierdzenie, że któraś funkcja (widmo) „pasuje” do innej, to znany problem już tylko numeryczny. Przedstawiona tu metoda zaowocowała nieprawdopodobnym wzrostem dokładności wyznaczeń prędkości radialnych, można mianowicie mierzyć prędkość radialną z dokładnością rzędu kilku metrów na sekundę! Co prawda trzeba przyznać, że metoda działa dla widm zawierających wiele ostrych linii, czyli tylko dla gwiazd chłodnych (późnych typów widmowych).

Po co to wszystko?

Pomiary zmian prędkości radialnych gwiazd podwójnych pozwalają astronomom wyznaczyć masy gwiazd stanowiących dany układ. Najczęściej jest tak, że widoczny jest ruch tylko jednej, jaśniejszej gwiazdy. Analiza zmian prędkości radialnych pozwala wyznaczyć w takim wypadku masę mniejszej, niewidocznej gwiazdy (o ile wiadomo, jaką masę ma widoczna). Nietrudno już przewidzieć, że tym składnikiem niewidocznym może równie dobrze być planeta. Np. 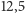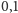by odkryć z daleka „naszego” Jowisza, należało by zmierzyć amplitudę zmian prędkości radialnej Słońca wynoszącą  m/s, zaś do „odkrycia” Ziemi trzeba by móc zmierzyć odpowiednio  m/s. Jest to jeszcze niewykonalne, co gorsza, metoda ta wymaga czasu porównywalnego z okresem orbitalnym planety, który dla Jowisza wynosi blisko 12 lat. Niemniej początek odkrywania planet został już zrobiony (Aleksander Wolszczan w 1992 roku). Dziś znamy 185 planet krążących wokół innych słońc, a 173 z nich odkryto właśnie techniką precyzyjnych pomiarów prędkości radialnych. Celem prowadzonych obecnie dużych projektów obserwacyjnych jest – ze zrozumiałych względów – poszukiwanie planet podobnych do Ziemi. Jednym z nich jest projekt realizowany we współpracy naukowców z Torunia i z Pensylwanii, którego celem jest poszukiwanie planet przy czerwonych olbrzymach, czyli przy gwiazdach takich, jaką Słońce stanie się za kilka miliardów lat. Zresztą znajdowanie planet przez toruńczyków ma długą historię. Wszak to Kopernik „wstrzymawszy Słońce” nadał Ziemi (i pięciu innym ciałom) charakter planet. Być może program poszukiwania planet przy czerwonych olbrzymach pozwoli podtrzymać tę tradycję.