Mała Delta
Wyznaczanie odległości, promienia orbity i rozmiarów Wenus

Wenus w naturalnych kolorach
Wielką przyjemność i satysfakcję sprawia obserwowanie przyrody. Nieporównanie większą – obserwowanie jej z poczuciem zrozumienia. Jednak największą odczuwa się chyba w trakcie samodzielnego jej poznawania. Jak wielką satysfakcję może sprawić wyznaczenie odległości do Wenus? Nie dowiesz się, jeśli nie spróbujesz tego dokonać. A warto, bo doświadczysz nie tylko satysfakcji badawczej...
Oglądając Wenus jaśniejącą na tle ciemniejącego nieba w oprawie żółtych, pomarańczowych i czerwonych zórz, poczujesz się wyróżniony, uczestnicząc w niezwykłym plastycznie spektaklu. A jeśli tak się zdarzy, że w pobliżu Wenus pojawi się jeszcze wąski sierp Księżyca, to bacz, byś nie został astronomem.
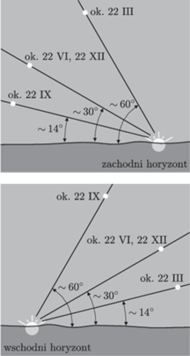
Rys. 1 Wczesną wiosną tuż po zachodzie Słońca (lub jesienią przed wschodem) kąt pomiędzy horyzontem a płaszczyzną, w której planety obiegają Słońce, jest największy. Z tego powodu w tych okresach takiej samej odległości kątowej Wenus od Słońca odpowiada największa wysokość Wenus ponad horyzontem – Wenus jest wtedy najlepiej widoczna.
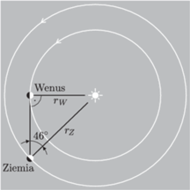
Rys. 2 Konfiguracja Ziemi, Wenus i Słońca w chwili maksymalnego kątowego oddalenia Wenus od Słońca.
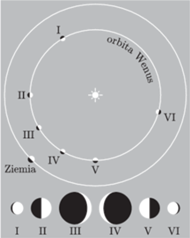
Rys. 3 Kątowe rozmiary tarczy Wenus oraz kształt oświetlonej części jej globu zależą od jej położenia względem Słońca i Ziemi.
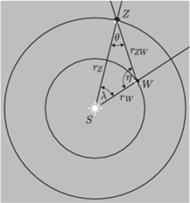
Rys. 4 Wyznaczenie aktualnej odległości Wenus–Ziemia
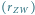 i promienia orbity
Wenus
i promienia orbity
Wenus
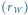 sprowadza się do rozwiązania trójkąta, którego wierzchołkami są Słońce,
Wenus i Ziemia.
sprowadza się do rozwiązania trójkąta, którego wierzchołkami są Słońce,
Wenus i Ziemia.
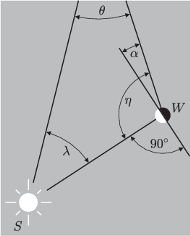
Rys. 5 Powiększony fragment rysunku 4.
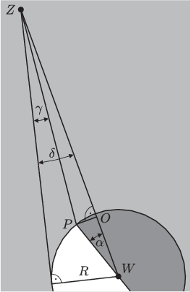
Rys. 6 Widok na Wenus
 i pozycję obserwatora
i pozycję obserwatora
 z kierunku
prostopadłego do płaszczyzny wyznaczonej przez położenia Ziemi, Wenus i Słońca.
z kierunku
prostopadłego do płaszczyzny wyznaczonej przez położenia Ziemi, Wenus i Słońca.
Wykonanie opisanego tu pomiaru nie będzie wymagało znajomości
astronomicznej kuchni; potrzebna będzie jednak amatorska luneta lub teleskop.
Jeśli dotychczas zupełnie nie zwracałeś uwagi na niebo, to przygotowania do
zasadniczego pomiaru wypada zacząć od nabycia umiejętności odnajdywania
Wenus na niebie. Zadanie to bardzo ułatwia ogromna jasność Wenus
(w porównaniu z gwiazdami) i jej zawsze niewielka kątowa odległość od
Słońca. Nigdy nie przekracza ona
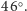 Gdy jest mniejsza niż
15-20 stopni, to mimo wielkiej jasności nie zobaczymy jej ze względu na dużą
jasność tła nieba. Możliwość obserwowania Wenus powtarza się
cyklicznie – takie samo jej położenie względem Słońca powtarza się po
około
Gdy jest mniejsza niż
15-20 stopni, to mimo wielkiej jasności nie zobaczymy jej ze względu na dużą
jasność tła nieba. Możliwość obserwowania Wenus powtarza się
cyklicznie – takie samo jej położenie względem Słońca powtarza się po
około
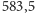 dobach. W tym czasie wystąpią dwa okresy dobrej
widoczności Wenus trwające po około 6 miesięcy. W jednym z nich
Wenus będzie widoczna na niebie po lewej stronie Słońca (na wschód
od niego) i wtedy można ją obserwować po zachodzie Słońca nad
południowo-zachodnim horyzontem. W takiej konfiguracji Wenus jest
nazywana Gwiazdą Wieczorną. Po krótkim, bo około miesięcznym okresie
nieobecności na niebie, Wenus pojawi się po prawej stronie Słońca (na zachód
od niego) i wtedy będzie widoczna przed wschodem Słońca, ponad
południowo-wschodnim horyzontem. Także w tym położeniu względem
Słońca można ją oglądać przez blisko 6 miesięcy. W tym okresie nazywamy
ją Jutrzenką. Po upływie tego okresu Wenus ponownie przestaje być widoczna,
lecz tym razem aż na 6 miesięcy. Po tym opisany cykl powtarza się.
Położenie Wenus względem Słońca, determinujące jej widoczność, podaje
każdy program komputerowy prezentujący niebo. Przybliżone daty
maksymalnego kątowego oddalenia Wenus od Słońca można jednak
wyznaczyć z następującego prostego wzoru:
dobach. W tym czasie wystąpią dwa okresy dobrej
widoczności Wenus trwające po około 6 miesięcy. W jednym z nich
Wenus będzie widoczna na niebie po lewej stronie Słońca (na wschód
od niego) i wtedy można ją obserwować po zachodzie Słońca nad
południowo-zachodnim horyzontem. W takiej konfiguracji Wenus jest
nazywana Gwiazdą Wieczorną. Po krótkim, bo około miesięcznym okresie
nieobecności na niebie, Wenus pojawi się po prawej stronie Słońca (na zachód
od niego) i wtedy będzie widoczna przed wschodem Słońca, ponad
południowo-wschodnim horyzontem. Także w tym położeniu względem
Słońca można ją oglądać przez blisko 6 miesięcy. W tym okresie nazywamy
ją Jutrzenką. Po upływie tego okresu Wenus ponownie przestaje być widoczna,
lecz tym razem aż na 6 miesięcy. Po tym opisany cykl powtarza się.
Położenie Wenus względem Słońca, determinujące jej widoczność, podaje
każdy program komputerowy prezentujący niebo. Przybliżone daty
maksymalnego kątowego oddalenia Wenus od Słońca można jednak
wyznaczyć z następującego prostego wzoru:
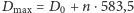 doby,
w którym
doby,
w którym
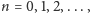 zaś
zaś
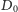 jest datą 27 marca 2012 r. dla
obserwacji prowadzonych o zmierzchu, lub datą 15 sierpnia 2012 r. w przypadku
obserwacji prowadzonych o świcie. W pierwszym przypadku, gdy Wenus jest
widoczna o zmierzchu, data
jest datą 27 marca 2012 r. dla
obserwacji prowadzonych o zmierzchu, lub datą 15 sierpnia 2012 r. w przypadku
obserwacji prowadzonych o świcie. W pierwszym przypadku, gdy Wenus jest
widoczna o zmierzchu, data
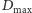 przypada na około cztery miesiące
po chwili, gdy Wenus zaczęła być widoczna o tej porze doby i na dwa
miesiące przed końcem tego okresu jej widoczności. Jeśli Wenus jest
widoczna o świcie, to data
przypada na około cztery miesiące
po chwili, gdy Wenus zaczęła być widoczna o tej porze doby i na dwa
miesiące przed końcem tego okresu jej widoczności. Jeśli Wenus jest
widoczna o świcie, to data
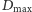 przypada na około dwa miesiące po
tym, jak zaczęła być widoczna przed wschodem Słońca, i na cztery
miesiące przed momentem, gdy o tej porze doby przestanie być już
widoczna.
przypada na około dwa miesiące po
tym, jak zaczęła być widoczna przed wschodem Słońca, i na cztery
miesiące przed momentem, gdy o tej porze doby przestanie być już
widoczna.
Przygotowania do obserwacji Wenus wymagają podania jeszcze jednej użytecznej informacji. Pośród cyklicznie występujących okresów widoczności najkorzystniejsze są te, w których znaczne kątowe oddalenie Wenus od Słońca przypada wczesną wiosną (gdy Wenus jest Gwiazdą Wieczorną) lub wczesną jesienią (gdy Wenus jest Jutrzenką). W tych okresach kąt pomiędzy horyzontem a płaszczyzną, w której Ziemia i inne planety obiegają Słońce, jest bowiem największy. Z tego powodu dla takiej samej odległości kątowej Wenus od Słońca jej kątowa wysokość ponad horyzontem będzie wyjątkowo duża, co w znacznym stopniu poprawia jej widoczność (Rys. 1).
Powróćmy na chwilę do podanej już wartości maksymalnej kątowej
odległości Wenus od Słońca, tj.
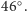 Jej samodzielne wyznaczenie
i potwierdzenie, iż jest niemal jednakowa podczas każdego oddalenia,
wymaga co prawda długiego oczekiwania, lecz jest łatwe do wykonania
i ma poważne konsekwencje. Wielkość tego kąta świadczy bowiem
o tym, że orbita Wenus zawiera się wewnątrz orbity Ziemi. Natomiast
powtarzalność tej wartości upoważnia nas do stwierdzenia, iż orbita Wenus
jest niemal dokładnie kołowa. Ponieważ maksymalne oddalenie Wenus od
Słońca ma miejsce wtedy, gdy Słońce, Wenus i Ziemia tworzą trójkąt
prostokątny z Wenus ulokowaną w wierzchołku kąta prostego (patrz Rys. 2), to
Jej samodzielne wyznaczenie
i potwierdzenie, iż jest niemal jednakowa podczas każdego oddalenia,
wymaga co prawda długiego oczekiwania, lecz jest łatwe do wykonania
i ma poważne konsekwencje. Wielkość tego kąta świadczy bowiem
o tym, że orbita Wenus zawiera się wewnątrz orbity Ziemi. Natomiast
powtarzalność tej wartości upoważnia nas do stwierdzenia, iż orbita Wenus
jest niemal dokładnie kołowa. Ponieważ maksymalne oddalenie Wenus od
Słońca ma miejsce wtedy, gdy Słońce, Wenus i Ziemia tworzą trójkąt
prostokątny z Wenus ulokowaną w wierzchołku kąta prostego (patrz Rys. 2), to
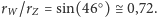 Ogromnym mankamentem tej metody
wyznaczenia promienia orbity Wenus, utrudniającym bardzo samodzielne
jej powtórzenie, jest konieczność bardzo długiego oczekiwania na
właściwy moment i wielokrotne powtarzanie pomiaru. Okazuje się
jednak, że przyjęcie dwóch założeń dotyczących toru ruchu Wenus oraz
dostęp do amatorskiej lunety lub teleskopu pozwalają w prosty sposób
i w dowolnym momencie wyznaczyć nie tylko promień orbity Wenus, ale
i jej aktualną odległość. Przyjmijmy więc za prawdę, iż orbita Wenus
jest niemal dokładnie kołowa, a jej nachylenie do płaszczyzny orbity
Ziemi – zaniedbywalnie małe. W opisanej niżej metodzie wykorzystane
będzie zjawisko możliwe do zaobserwowania nawet przez niewielką
lunetę. Ponieważ orbita Wenus jest obejmowana w całości orbitą Ziemi,
to jasna część globu Wenus widoczna przez lunetę będzie zmieniała
kształt i wielkość – powinniśmy widzieć ją w różnych fazach
(patrz rysunek 3). Zjawisko to po raz pierwszy zaobserwował Galileusz,
przyczyniając się w ten sposób do obalenia geocentrycznego modelu organizacji
świata.
Ogromnym mankamentem tej metody
wyznaczenia promienia orbity Wenus, utrudniającym bardzo samodzielne
jej powtórzenie, jest konieczność bardzo długiego oczekiwania na
właściwy moment i wielokrotne powtarzanie pomiaru. Okazuje się
jednak, że przyjęcie dwóch założeń dotyczących toru ruchu Wenus oraz
dostęp do amatorskiej lunety lub teleskopu pozwalają w prosty sposób
i w dowolnym momencie wyznaczyć nie tylko promień orbity Wenus, ale
i jej aktualną odległość. Przyjmijmy więc za prawdę, iż orbita Wenus
jest niemal dokładnie kołowa, a jej nachylenie do płaszczyzny orbity
Ziemi – zaniedbywalnie małe. W opisanej niżej metodzie wykorzystane
będzie zjawisko możliwe do zaobserwowania nawet przez niewielką
lunetę. Ponieważ orbita Wenus jest obejmowana w całości orbitą Ziemi,
to jasna część globu Wenus widoczna przez lunetę będzie zmieniała
kształt i wielkość – powinniśmy widzieć ją w różnych fazach
(patrz rysunek 3). Zjawisko to po raz pierwszy zaobserwował Galileusz,
przyczyniając się w ten sposób do obalenia geocentrycznego modelu organizacji
świata.
Rysunek 4 przedstawia pozycje Wenus
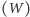 , Słońca
, Słońca
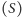 i Ziemi
i Ziemi
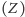 . Płaszczyzna tego rysunku, jak również rysunków 5 i 6, pokrywa
się z płaszczyzną orbity Wenus i Ziemi. Wyznaczenie odległości z Ziemi do
Wenus
. Płaszczyzna tego rysunku, jak również rysunków 5 i 6, pokrywa
się z płaszczyzną orbity Wenus i Ziemi. Wyznaczenie odległości z Ziemi do
Wenus
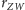 oraz promienia orbity Wenus
oraz promienia orbity Wenus
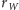 sprowadza się
do rozwiązania trójkąta
sprowadza się
do rozwiązania trójkąta
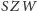 widocznego na rysunku 4. Kąt
widocznego na rysunku 4. Kąt
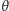 w tym trójkącie można zmierzyć podczas bezpośredniej
obserwacji. Natomiast kąt
w tym trójkącie można zmierzyć podczas bezpośredniej
obserwacji. Natomiast kąt
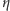 można, jak się za chwilę okaże, wyznaczyć
na podstawie kształtu obserwowanej fazy Wenus. Z rysunku 5 wynika bowiem,
że
można, jak się za chwilę okaże, wyznaczyć
na podstawie kształtu obserwowanej fazy Wenus. Z rysunku 5 wynika bowiem,
że
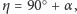 zaś kąt
zaś kąt
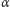 można wyznaczyć z trójkątów
można wyznaczyć z trójkątów
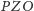 oraz
oraz
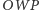 widocznych na rysunku 6.
widocznych na rysunku 6.
Wynikają z nich następujące zależności:
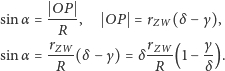
Ponieważ
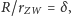 więc ostatecznie
więc ostatecznie
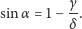
Otrzymana zależność oraz związek
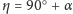 pozwalają
wyznaczyć kąt
pozwalają
wyznaczyć kąt
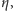 jeśli obserwacyjnie określimy stosunek kąta
jeśli obserwacyjnie określimy stosunek kąta
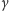 do
do
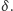 Jeśli kąty
Jeśli kąty
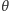 i
i
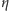 uznamy już za znane, to
ostateczne rozwiązanie problemu otrzymamy, stosując twierdzenie sinusów do
trójkąta
uznamy już za znane, to
ostateczne rozwiązanie problemu otrzymamy, stosując twierdzenie sinusów do
trójkąta
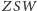 widocznego na rysunku 4:
widocznego na rysunku 4:
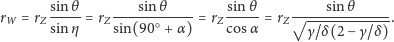 | (1) |
Stosując po raz drugi twierdzenie sinusów do tego trójkąta, obliczymy
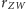 :
:
Ponieważ w zależnościach (1) i (2) kąty
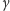 i
i
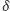 występują
wyłącznie w postaci ilorazu, więc do wyznaczenia
występują
wyłącznie w postaci ilorazu, więc do wyznaczenia
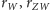 nie jest
konieczne określanie ich wartości w jednostkach kątowych. Używane
jednostki muszą być jednak proporcjonalne do jednostek kątowych. Kątowa
wartość
nie jest
konieczne określanie ich wartości w jednostkach kątowych. Używane
jednostki muszą być jednak proporcjonalne do jednostek kątowych. Kątowa
wartość
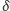 będzie natomiast potrzebna do wyznaczenia promienia
planety
będzie natomiast potrzebna do wyznaczenia promienia
planety
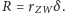 Wartość
Wartość
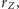 występującą w związkach (1)
i (2), można potraktować jako znaną, przyjmując
występującą w związkach (1)
i (2), można potraktować jako znaną, przyjmując
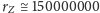 km
lub, wzorem naszych poprzedników,
km
lub, wzorem naszych poprzedników,
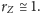
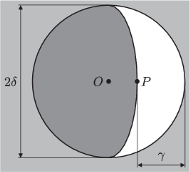
Rys. 7 Tarcza Wenus widoczna z Ziemi.
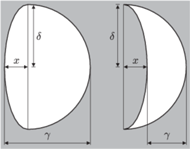
Rys. 8 Stosunek
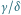 można ocenić wprost lub obliczyć po uprzedniej wzrokowej
ocenie stosunku
można ocenić wprost lub obliczyć po uprzedniej wzrokowej
ocenie stosunku
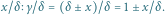
Obserwacyjna część zadania będzie polegała na samodzielnym wyznaczeniu
wartości
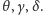 Ze względu na dużą jasność Wenus na ogół
widać ją jeszcze przed zachodem Słońca lub po jego wschodzie. W takim
przypadku możliwy jest bezpośredni pomiar kąta
Ze względu na dużą jasność Wenus na ogół
widać ją jeszcze przed zachodem Słońca lub po jego wschodzie. W takim
przypadku możliwy jest bezpośredni pomiar kąta
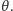 Z wystarczającą
dokładnością można go zmierzyć za pomocą bardzo prostego kątomierza,
który można wykonać samodzielnie.
Z wystarczającą
dokładnością można go zmierzyć za pomocą bardzo prostego kątomierza,
który można wykonać samodzielnie.
Z dwóch listew, o długości ok. 1 m, zbudować coś, co przypominało będzie duży cyrkiel. Na każdej z listew zaznaczyć punkt jednakowo odległy od osi obrotu. W te miejsca można wbić gwoździki ułatwiające celowanie. Kąt rozchylenia listew obliczać po zmierzeniu odcinka pomiędzy zaznaczonymi na listwach punktami (gwoździkami), stanowiącej podstawę trójkąta równoramiennego o znanej długości ramion.
Pomiar tego kąta będzie jeszcze łatwiejszy, jeśli luneta wykorzystywana do
obserwacji będzie osadzona na tzw. montażu paralaktycznym ustawionym tak,
by jedna z osi obrotu mechanizmu była równoległa (choćby w przybliżeniu)
do osi obrotu nieba. Ponieważ kątowe odległości Słońca i Wenus od bieguna
nieba są zazwyczaj bardzo zbliżone, to kąt pomiędzy tymi obiektami można
utożsamiać z jego rzutem na płaszczyznę prostopadłą do osi obrotu nieba.
Skoro tak, to jako rozwartość kąta
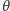 można przyjmować różnicę
wskazań na skali kręgu pomiarowego związanego z osią obrotu równoległą do
osi obrotu nieba. Celując lunetą w Słońce, należy zasłonić obiektyw,
a jako wskaźnik poprawności kierunku lunety wykorzystywać jej
cień.
można przyjmować różnicę
wskazań na skali kręgu pomiarowego związanego z osią obrotu równoległą do
osi obrotu nieba. Celując lunetą w Słońce, należy zasłonić obiektyw,
a jako wskaźnik poprawności kierunku lunety wykorzystywać jej
cień.
Do pomiaru kątów
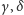 będzie potrzebna luneta lub teleskop
zwierciadlany. Skutkiem małych wysokości ponad horyzontem, na jakich bywa
widoczna Wenus, jej obraz jest zawsze bardzo niestabilny. Z tego powodu
precyzyjny pomiar kątów
będzie potrzebna luneta lub teleskop
zwierciadlany. Skutkiem małych wysokości ponad horyzontem, na jakich bywa
widoczna Wenus, jej obraz jest zawsze bardzo niestabilny. Z tego powodu
precyzyjny pomiar kątów
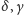 jest trudny. Najdokładniej można to
zrobić za pomocą lunety wyposażonej w mikrometr.
jest trudny. Najdokładniej można to
zrobić za pomocą lunety wyposażonej w mikrometr.
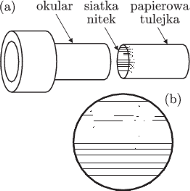
Rys. 9 Prosty mikrometr: (a) schemat budowy, (b) widok nitek w okularze.
Choćby taki, jak na rysunku 9: Z papieru wykonać rurkę o średnicy pasującej do wewnętrznej średnicy tulejki okularu, o długości nieco większej niż długość tulejki. Na jedną z otwartych podstaw rurki nakleić mniej więcej równolegle kilkanaście cienkich włókien (np. najcieńsze fragmenty włókien z tkanin syntetycznych). Papierową tulejkę wsunąć do rurki okularu, na taką głębokość, by przez okular włókna były ostro widoczne. Po skierowaniu okularu na jasne tło należy wykonać dokładny rysunek widocznych włókien – należy narysować je dokładnie tak, jak je widać, zachowując skalę odstępów, ich ewentualne nierównoległości i zanieczyszczenia (ważne jest bowiem, by nitki widoczne przez okular i na rysunku można było identyfikować). Na rysunku tym można będzie zaznaczać położenia końców odcinków odpowiadających kątom, które należy zmierzyć.
Ponieważ kąty
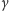 i
i
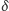 występują (w zależnościach (1) i (2))
wyłącznie w postaci ilorazu
występują (w zależnościach (1) i (2))
wyłącznie w postaci ilorazu
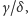 nie będzie konieczna znajomość
kątowej skali takiego mikrometru. Dla tych, którzy nie mają mikrometru,
pocieszeniem może być fakt, że ze względu na nieostrość obrazu Wenus
i jego nieustanne drgania, wywoływane turbulencjami atmosferycznymi,
dokładność oceny stosunku
nie będzie konieczna znajomość
kątowej skali takiego mikrometru. Dla tych, którzy nie mają mikrometru,
pocieszeniem może być fakt, że ze względu na nieostrość obrazu Wenus
i jego nieustanne drgania, wywoływane turbulencjami atmosferycznymi,
dokładność oceny stosunku
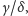 jaką można uzyskać z osobnych
pomiarów mikrometrycznych każdego z kątów, nie jest lepsza od
dokładności uzyskiwanej przy ocenie wartości tego stosunku metodą „na oko”
(patrz Rys. 8).
jaką można uzyskać z osobnych
pomiarów mikrometrycznych każdego z kątów, nie jest lepsza od
dokładności uzyskiwanej przy ocenie wartości tego stosunku metodą „na oko”
(patrz Rys. 8).
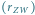 i promienia orbity
Wenus
i promienia orbity
Wenus
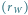 sprowadza się do rozwiązania trójkąta, którego wierzchołkami są Słońce,
Wenus i Ziemia.
sprowadza się do rozwiązania trójkąta, którego wierzchołkami są Słońce,
Wenus i Ziemia.
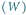 i pozycję obserwatora
i pozycję obserwatora
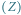 z kierunku
prostopadłego do płaszczyzny wyznaczonej przez położenia Ziemi, Wenus i Słońca.
z kierunku
prostopadłego do płaszczyzny wyznaczonej przez położenia Ziemi, Wenus i Słońca.
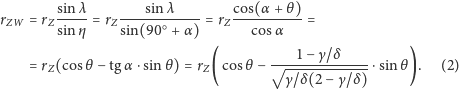
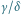 można ocenić wprost lub obliczyć po uprzedniej wzrokowej
ocenie stosunku
można ocenić wprost lub obliczyć po uprzedniej wzrokowej
ocenie stosunku