Zadanie 1. Przyjmując, że po orbicie keplerowskiej, w ruchu obiegowym wokół Słońca porusza się środek masy układu Ziemia-Księżyc (barycentrum), oblicz ekstremalne wartości, jakie może przyjmować odległość pomiędzy środkiem Ziemi i środkiem Słońca. W rozwiązaniu przyjmij, że orbity Księżyca i Ziemi są współpłaszczyznowe. Potrzebne dane liczbowe wyszukaj samodzielnie.

Zadanie 2. Jasność obserwowana gwiazdy zmiennej zaćmieniowej przyjmuje wartości z przedziału: 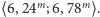 Krzywa jasności tej gwiazdy wykazuje płaskie dna, a wszystkie minima jasności mają taką samą głębokość. Zakładając, że gwiazdy są kuliste, a zaćmienia gwiazd zachodzą centralnie, oblicz, jaki procent czasu trwania dowolnego zaćmienia zajmuje płaskie dno.

Zadanie 3. Główną część systemu nawigacyjnego GPS (Global Positioning System) stanowią satelity obiegające Ziemię po okręgach nachylonych do płaszczyzny równika pod kątem 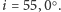 Okres obiegu każdego satelity wynosi pół doby gwiazdowej: 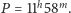 Jak długo, podczas jednego obiegu, satelita tego systemu może przebywać nad horyzontem astronomicznym dla obserwatora znajdującego się na ziemskim biegunie i na jaką maksymalną wysokość kątową może się tam wznieść ponad horyzont? W rozwiązaniu pomiń wpływ oddziaływań perturbacyjnych i spłaszczenie Ziemi oraz przyjmij jako dodatkowe dane liczbowe: promień Ziemi 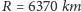i wartość drugiej prędkości kosmicznej

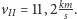
Zadanie 4. Odkrywanie planet jest tym łatwiejsze, im planeta ma krótszy okres obiegu oraz im mniej masywna jest jej macierzysta gwiazda. Wiedząc, że dla gwiazd ciągu głównego zachodzi przybliżona proporcjonalność: 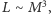 gdzie 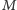 jest masą, a 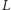 – mocą promieniowania gwiazdy, określ, jakiego zakresu okresów obiegu i odległości od macierzystej gwiazdy należy spodziewać się w przypadku planet obiegających gwiazdy o masach mniejszych od masy Słońca, a więc gwiazdy w zakresie od 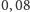 do jednej masy Słońca, a ilość energii docierającej od gwiazdy w jednostce czasu do jednostkowej powierzchni planety (prostopadłej do kierunku padania promieni) jest równa stałej słonecznej na Ziemi. Potrzebne dane liczbowe dotyczące uniwersalnych stałych i parametrów Układu Słonecznego wyszukaj samodzielnie.

Zadanie 5. Pływy oraz perturbacje powodują zmianę elementów orbit: Księżyca wokół Ziemi (Z-K) oraz Ziemi wokół Słońca (S-Z). Ponadto, na skutek ewolucyjnych zmian Słońce zwiększa swój promień o 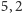% na miliard lat. W wyniku tych zmian warunki obserwacji całkowitych zaćmień Słońca z powierzchni Ziemi również ulegają modyfikacjom. Przyjmując, że mimośrody orbit oscylują w zakresach podanych w tabelce, a wielkie półosie orbit i promień Słońca zwiekszają się liniowo w czasie, oblicz, kiedy nastąpi ostatnie całkowite zaćmienie Słońca widoczne z powierzchni Ziemi.

Zadanie 6. W odległości odpowiadającej przesunięciu ku czerwieni 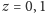 zaobserwowano galaktykę o średnicy kątowej 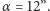 Udało się również zmierzyć przesunięcie ku czerwieni zewnętrznych fragmentów tej galaktyki. Różniło się ono od przesunięcia średniego  o 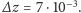  Przyjmując, że różnica ta jest spowodowana ruchem wokół centrum, a oś obrotu galaktyki jest prostopadła do linii widzenia, oblicz masę obserwowanej galaktyki. Zakładamy dodatkowo, że rozkład materii jest w tej galaktyce sferycznie symetryczny, a ruch gwiazd jest kołowy z prędkościami nierelatywistycznymi.