Wszak np. z daleka gwiazda jasna (mówimy: o dużej jasności absolutnej) będzie wyglądać tak, jak słaba z bliska. Słońce i Księżyc mają niemal identyczne rozmiary kątowe, ale Słońce jest 400 razy dalej, a więc tyleż razy większe, jest więc zapewne ciałem o zupełnie innej naturze niż Księżyc itd. Jak doszło do poznania odległości ciał, z których tylko nieliczne najbliższe człowiek zdołał osiągnąć?

Odległości ciał najbliższych mierzy się „najuczciwiej” w tym sensie, że nie trzeba do tego żadnych założeń, np. co do natury danego ciała. Pomińmy metody laserowe i radarowe ze względu na ich dość ograniczone możliwości. Standardowo natomiast korzysta się (korzystało) z tego, że badany obiekt, oglądany z dwóch miejsc, jest widoczny w nieco różnych miejscach tła. W przypadku oczu nazywa się to efektem stereoskopowym. W zasięgu kilkudziesięciu metrów automatycznie rozróżniamy, co jest bliżej, a co dalej. Jeżeli oczy sztucznie rozsuniemy na większą odległość, np. budując dalmierz, to stereoskopowe widzenie sięgnie kilku kilometrów. Mierzy się tu kąt między kierunkami na obiekt z jednego i drugiego „oka”. Znając bazę, czyli rozstaw oczu (lub obiektywów dalmierza, lub dwóch obserwatoriów), można na podstawie prostej geometrii ocenić odległość obserwowanego obiektu. Kąt, pod jakim z obiektu byłoby widać promień Ziemi, nazywa się paralaksą geocentryczną tego obiektu. Jej znajomość jest równoważna znajomości odległości ciała.

W ten sposób zmierzono odległości stosunkowo bliskich ciał: Księżyca, planet, planetoid. Metoda ta do gwiazd nie sięga, bo Ziemia jest za mała. Udało się jednak wykorzystać fakt, że w odstępie pół roku Ziemia przemieszcza się do miejsca odległego o średnicę okołosłonecznej orbity od miejsca startowego. A jest to – jak by nie było – 300 mln km. Taki „rozstaw oczu” umożliwił zmierzenie tzw. paralaks heliocentrycznych wielu gwiazd. Okazało się (w 1838 roku), że paralaksa heliocentryczna (dokładniej: to kąt, pod jakim z gwiazdy byłoby widać promień ziemskiej orbity) najbliższej gwiazdy jest kątem mniejszym od sekundy łuku. Dlatego pomiaru tego dokonano tak późno. Gwiazdy okazały się znacznie bardziej odległe, niż się ówczesnym astronomom zdawało. Odległość odpowiadająca paralaksie heliocentrycznej równej 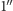to tzw. parsek (pc; łatwo zgadnąć, skąd się ta nazwa wzięła). Wynosi on ponad 200 000 j.a. (tj. promieni ziemskiej orbity), albo w przybliżeniu 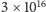m, albo 3,26 roku świetlnego. Z powierzchni Ziemi mierzono paralaksy do 0,01 sekundy łuku, czyli odległości gwiazd do 100 pc. Satelita Hipparcos (od ang. High Precision Parallax Collecting Satellite) był w stanie mierzyć paralaksy do 0,001 sekundy łuku (bo spoza atmosfery), a więc odległości do 1 kpc.

Dalej geometria nie sięga, bo orbita Ziemi jest za mała. Ale przy okazji tych pomiarów poznano cechy fizyczne mnóstwa gwiazd, w szczególności ich jasności absolutne. Bo jasność obserwowana 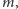którą mierzy się przy każdej okazji, zależy od jasności absolutnej 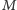i odległości gwiazdy według wzoru

(odległość jest tu wyrażona w parsekach). Jeżeli dla wielu gwiazd zmierzyć odległości za pomocą paralaksy, to mając ich jasności 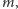można wyznaczyć ich jasności absolutne 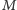i sporządzić np. diagram Hertzsprunga-Russella, co zostało zrobione na poczatku XX wieku. Przyjmując, że odległe gwiazdy są takie, jak w pobliżu Słońca, można wzór wykorzystać inaczej. Teraz znając 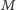na podstawie widma gwiazdy (i jak zawsze – z pomiaru jasności), oblicza się odległość gwiazdy. Nazywa się to wyznaczeniem paralaksy spektroskopowej (bo 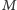określa się z widma). Domyślamy się, że ten w zasadzie łatwy sposób wyznaczania odległości komplikuje materia międzygwiazdowa. Wzór powyższy jest słuszny, jeżeli przestrzeń między obiektem a obserwatorem jest pusta, czyli gdy nie ma po drodze od obiektu strat światła. Wiadomo, że te straty są i wiadomo, jak je uwzględnić. Jednak nie będziemy się tą sprawą tu zajmować.

Przytoczony tu wzór można zastosować do dowolnych kosmicznych źródeł światła, jeżeli tylko skądinąd znamy ich moc, czyli jasność absolutną. Wzór ten zaowocował wyznaczeniem odległości pobliskich galaktyk na podstawie pomiaru jasności różnych wybranych gwiazd w tych galaktykach (cefeid, nowych, supernowych). Wreszcie 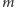i 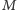 mogą w tym wzorze równie dobrze oznaczać jasność (obserwowaną i absolutną) całej galaktyki, gdyż z obserwacji ich gwiazd udało się ocenić jasności absolutne niezbyt odległych galaktyk.

Natura podsunęła inny niezależny sposób oceniania odległości galaktyk. Edwin Hubble na początku XX wieku odkrył mianowicie, że im odleglejsza (sądząc po jasności ) jest galaktyka, tym szybciej od nas się oddala. Prędkości (radialne) wyznacza się na podstawie obserwowanego przesunięcia widma galaktyki. Bowiem zjawisko Dopplera powoduje, że wszelkie linie w widmie oddalającej się galaktyki wypadają nieco bardziej ku czerwieni, niż gdyby obserwowana galaktyka nie poruszała się. Przyczyną tej „ucieczki galaktyk” jest ekspansja całego Wszechświata, a w każdym razie tak ją zinterpretowano i o tym przekonana jest większość astronomów. Sam Hubble stwierdził (w 1929 roku) proporcjonalność prędkości ucieczki 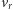do odległości galaktyki:

gdzie H jest współczynnikiem proporcjonalności, nazwanym później stałą Hubble’a.

Z czasem prawo Hubble’a z odkrycia stało się narzędziem do wyznaczania odległości galaktyk. Mierzy się owo przesunięcie ku czerwieni

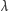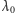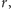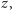
gdzie oznacza obserwowaną długość fali, a  długość fali, gdyby galaktyka była nieruchoma. Ono ostatecznie określa odległość ale… Otóż przeliczenie na prędkość i dalej na odległość jest tak proste jedynie dla niezbyt wielkich 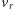i 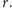 Dla dużych wartości – po pierwsze – należy stosować wzory zgodne z teorią względności (bo jeśli nie, to duże dawałoby prędkość galaktyki większą od prędkości światła, a obecnie obserwuje się galaktyki, których 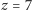), po drugie – sposób przeliczania na odległość zależy od modelu Wszechświata (np. charakteru ekspansji), wreszcie – po trzecie – dla obiektów odległych pojawiają się problemy z samym zdefiniowaniem odległości. Bo przecież dobrze by było, żeby kątowe rozmiary obiektu były odwrotnie proporcjonalne do jego odległości, a zarazem strumień jego promieniowania był odwrotnie proporcjonalny do kwadratu odległości (byłaby to tzw. odległość fotometryczna). Tymczasem we Wszechświecie, ekspandującym i „powyginanym” przez pole grawitacyjne zawartej w nim materii, nie ma takiej uniwersalnej odległości. Najczęściej mówi się o odległości fotometrycznej, bo w zasadzie można ją określić na podstawie jasności 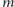galaktyki, o ile zna się niezbędne parametry Wszechświata. Żeby uniknąć tych dylematów, za „odległość” uważa się po prostu zmierzoną wartość ; w każdym razie tak robią obserwatorzy, zostawiając interpretację teoretykom.

Ilustracja zależności od jasności obserwowanej 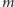galaktyk nazywa się diagramem Hubble’a. Dopasowywanie teoretycznych przewidywań do tego diagramu pozwala na testowanie konkurencyjnych modeli Wszechświata. Niestety, obserwacje skrajnie odległych galaktyk są trudne, a ich wyniki niepewne. A przecież Wszechświat rozciąga się poza
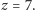Gdzieś tam w niezbadanych dotąd obszarach (żeby nie powiedzieć patetycznie – otchłaniach), odległych od nas o gigaparseki, powinny znajdować się protogalaktyki, kwazary, zgęszczenia materii, z których promieniowanie reliktowe już bez przeszkód do nas dotarło, miejsca, gdzie z protonów i elektronów powstał pierwotny wodór. 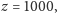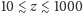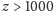Promieniowanie reliktowe, odpowiadające w przybliżeniu obserwujemy, ale nie sposób dziś przewidzieć, czy obszary pośrednie ( ) lub jeszcze dalsze ( ) zostaną kiedykolwiek poznane obserwacyjnie, czy sięgniemy do nich tylko teorią.

Odległościom kosmicznym poświęcona była Delta 10/2001.