Iloraz dwu liczb 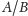to część całkowita 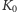oraz jakiś ułamek właściwy. Ten ułamek to jedność podzielona przez odwrotność ułamka, a ona to znowu jakaś inna część całkowita 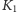plus inny ułamek właściwy. Do tego ułamka znowu stosuje się to, co powiedziano w poprzednim zdaniu itd. Zapisuje się to właśnie jako ułamek łańcuchowy

Jeżeli na starcie był iloraz stanowiący po prostu liczbę wymierną, to odpowiadający jej ułamek łańcuchowy będzie skończony, bo opisana tu procedura osiągnie koniec. Jeżeli iloraz był liczbą niewymierną, to ułamek będzie wprawdzie nieskończony, ale jego obcięcia (mówi się: redukty) będą wymiernymi przybliżeniami wyjściowego stosunku liczb. A to już może być interesujące.

Niech 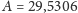oraz 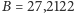będą wyrażonymi w dniach przybliżonymi długościami miesiąca synodycznego i smoczego. Miesiąc synodyczny to okres, po jakim powtarzają się fazy Księżyca, a smoczy to okres, po jakim Księżyc powraca do tego samego węzła orbity, tj. punktu, w którym jego orbita przecina ekliptykę. Żaden z nich nie jest równy okresowi obiegu Księżyca wokół Ziemi, ponieważ ani Słońce, ani węzły orbity nie są na niebie nieruchome. Znaczenie tych pojęć wynika stąd, że z ich pomocą można łatwo sformułować prawo rządzące zaćmieniami (Słońca lub Księżyca). Aby w ogóle nastąpiło zaćmienie, Księżyc musi znajdować się albo w nowiu, albo w pełni oraz blisko któregoś węzła. Jeżeli więc kiedyś nastąpiło zaćmienie, to w przyszłości zaćmienie nastąpi, gdy upłynie całkowita liczba miesięcy zarówno synodycznych, jak i smoczych – wszystko oczywiście w jakimś rozsądnym przybliżeniu. Długości miesięcy określone ze skończoną dokładnością dają iloraz wymierny, zatem odpowiadający mu ułamek łańcuchowy jest skończony, tylko nie wiadomo, jak długi. Jego początek to 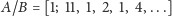. Obcięcie akurat na tej czwórce daje 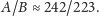 Wynik ten oznacza, że 242 miesiące smocze trwają tyle samo co 223 miesiące synodyczne, z błędem – co łatwo sprawdzić – zaledwie 0,03 dnia.

Okres ten, zwany sarosem, równy w przybliżeniu 6585,3 dni, znany był już w starożytności. Odkryto go prawdopodobnie metodą prób i błędów. Rzecz jasna, w czasie każdego sarosu wystąpi wiele innych zaćmień, ale te, które dzieli saros, stanowią regularną serię. Jednak przewidywanie zaćmień na tej podstawie na bardzo odległą przyszłość musi zawieść, bo przecież ta regularność to tylko przybliżenie.