Zadania z matematyki - X 2020»Zadanie 1653
o zadaniu...
- Zadanie pochodzi z artykułu Zadania z matematyki - X 2020
- Publikacja w Delcie: październik 2020
- Publikacja elektroniczna: 30 września 2020
Jaś wymyślił pewien wielomian 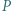 o nieujemnych współczynnikach całkowitych. Małgosia może pytać Jasia o wartość
o nieujemnych współczynnikach całkowitych. Małgosia może pytać Jasia o wartość 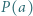 dla wybranego przez nią całkowitego argumentu
dla wybranego przez nią całkowitego argumentu 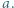 Ile pytań potrzebuje Małgosia, aby wyznaczyć wielomian
Ile pytań potrzebuje Małgosia, aby wyznaczyć wielomian 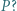

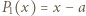
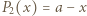
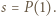
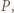
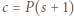 ; reprezentacja tej liczby w
; reprezentacja tej liczby w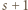
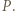
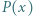 będzie wielomianem
będzie wielomianem 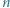 -tego stopnia
-tego stopnia 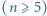 o współczynnikach całkowitych, mającym
o współczynnikach całkowitych, mającym 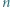 różnych pierwiastków całkowitych. Załóżmy, że 0 jest jednym z jego pierwiastków. Udowodnić, że wielomian
różnych pierwiastków całkowitych. Załóżmy, że 0 jest jednym z jego pierwiastków. Udowodnić, że wielomian 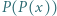 również ma dokładnie
również ma dokładnie  różnych pierwiastków całkowitych.
różnych pierwiastków całkowitych.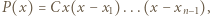 gdzie
gdzie 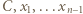 są liczbami całkowitymi. Oczywiście
są liczbami całkowitymi. Oczywiście 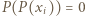 dla
dla 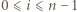 (przyjmujemy
(przyjmujemy 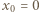 ). Załóżmy, że
). Załóżmy, że 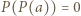 dla pewnego
dla pewnego 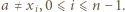 Wówczas
Wówczas 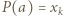 dla pewnego
dla pewnego 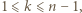 czyli
czyli 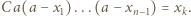 W tej sytuacji
W tej sytuacji 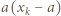 dzieli
dzieli 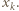 Załóżmy, że
Załóżmy, że 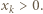 Z podzielności
Z podzielności 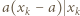 wnioskujemy kolejno
wnioskujemy kolejno 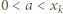 oraz
oraz 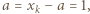 czyli
czyli 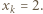 Jednak
Jednak 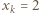 ma tylko 4 różne dzielniki całkowite, co przeczy równości
ma tylko 4 różne dzielniki całkowite, co przeczy równości 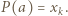 Przypadek
Przypadek 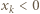 rozpatrujemy podobnie i w ten sposób kończymy dowód, że tylko pierwiastki wielomianu
rozpatrujemy podobnie i w ten sposób kończymy dowód, że tylko pierwiastki wielomianu 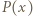 są całkowitymi pierwiastkami wielomianu
są całkowitymi pierwiastkami wielomianu 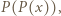 co dopełnia rozwiązanie.
co dopełnia rozwiązanie.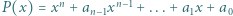 ma
ma  pierwiastków rzeczywistych (licząc z krotnościami). Wiedząc, że
pierwiastków rzeczywistych (licząc z krotnościami). Wiedząc, że 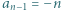 i
i 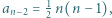 wyznaczyć
wyznaczyć 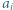 dla
dla 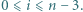
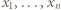 będą pierwiastkami
będą pierwiastkami 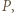 tzn.
tzn. 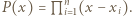 Korzystając ze wzorów Viète'a, mamy
Korzystając ze wzorów Viète'a, mamy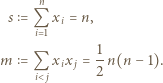
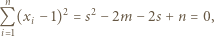
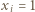 dla
dla 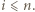 Pozostaje łatwe sprawdzenie, że wielomian
Pozostaje łatwe sprawdzenie, że wielomian 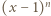 spełnia przedstawione w zadaniu warunki. Dlatego
spełnia przedstawione w zadaniu warunki. Dlatego 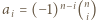 dla
dla 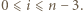
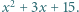 Następnie wszyscy uczniowie w klasie podchodzili kolejno do tablicy; każdy z nich zmniejszał albo zwiększał o jeden współczynnik przy
Następnie wszyscy uczniowie w klasie podchodzili kolejno do tablicy; każdy z nich zmniejszał albo zwiększał o jeden współczynnik przy  albo wyraz wolny trójmianu. Na koniec okazało się, że na tablicy widnieje trójmian
albo wyraz wolny trójmianu. Na koniec okazało się, że na tablicy widnieje trójmian 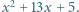 Udowodnić, że w pewnym momencie na tablicy był napisany trójmian o pierwiastkach całkowitych.
Udowodnić, że w pewnym momencie na tablicy był napisany trójmian o pierwiastkach całkowitych.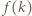 będzie wartością danego trójmianu w punkcie
będzie wartością danego trójmianu w punkcie 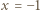 po zmianie współczynników przez
po zmianie współczynników przez 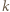 -tego ucznia i niech
-tego ucznia i niech 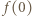 będzie wartością w -1 trójmianu napisanego przez nauczyciela. Zauważmy, że
będzie wartością w -1 trójmianu napisanego przez nauczyciela. Zauważmy, że 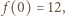 a
a 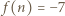 (gdzie
(gdzie 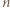 to numer ostatniego ucznia). Ponadto zachodzi nierówność
to numer ostatniego ucznia). Ponadto zachodzi nierówność 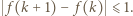 Rzeczywiście - jest to jasne, gdy zmieniamy wyraz wolny, zaś zmieniając o
Rzeczywiście - jest to jasne, gdy zmieniamy wyraz wolny, zaś zmieniając o 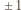 wartość współczynnika przy
wartość współczynnika przy 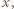 dodajemy lub odejmujemy 1 do wartości wielomianu w -1. W takim razie istnieje takie
dodajemy lub odejmujemy 1 do wartości wielomianu w -1. W takim razie istnieje takie 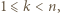 że
że 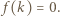 Zatem w pewnym momencie na tablicy był napisany trójmian
Zatem w pewnym momencie na tablicy był napisany trójmian 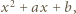 którego jednym z pierwiastków było -1; ze wzorów Viète'a wnosimy, że drugim jego pierwiastkiem była liczba całkowita
którego jednym z pierwiastków było -1; ze wzorów Viète'a wnosimy, że drugim jego pierwiastkiem była liczba całkowita 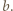
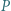 ma wszystkie współczynniki całkowite i dla każdej liczby naturalnej
ma wszystkie współczynniki całkowite i dla każdej liczby naturalnej 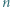 zachodzą nierówności
zachodzą nierówności 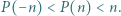 Wykazać, że
Wykazać, że 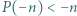 dla wszystkich naturalnych
dla wszystkich naturalnych 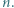
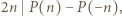 a z założeń
a z założeń 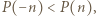 więc
więc 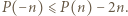
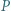 o współczynnikach całkowitych przyjmuje wartości nieparzyste dla pewnych dwóch kolejnych liczb naturalnych. Udowodnić, że ten wielomian nie ma pierwiastków będących liczbami całkowitymi.
o współczynnikach całkowitych przyjmuje wartości nieparzyste dla pewnych dwóch kolejnych liczb naturalnych. Udowodnić, że ten wielomian nie ma pierwiastków będących liczbami całkowitymi.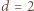 wywnioskujemy, że
wywnioskujemy, że 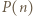 jest liczbą nieparzystą dla każdego całkowitego
jest liczbą nieparzystą dla każdego całkowitego 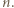
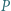 o współczynnikach całkowitych przyjmuje wartość
o współczynnikach całkowitych przyjmuje wartość 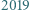 dla pięciu różnych argumentów będących liczbami całkowitymi. Dowieść, że ten wielomian nie ma pierwiastków całkowitych.
dla pięciu różnych argumentów będących liczbami całkowitymi. Dowieść, że ten wielomian nie ma pierwiastków całkowitych.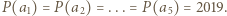 Liczby
Liczby 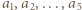 są różnymi pierwiastkami wielomianu
są różnymi pierwiastkami wielomianu 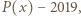 więc na mocy twierdzenia Bézouta
więc na mocy twierdzenia Bézouta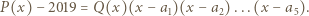
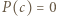 dla pewnego całkowitego
dla pewnego całkowitego 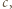 to liczba
to liczba 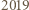 byłaby iloczynem sześciu liczb całkowitych, wśród których jest pięć różnych liczb.
byłaby iloczynem sześciu liczb całkowitych, wśród których jest pięć różnych liczb.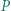 ma trzeci stopień i wszystkie współczynniki całkowite oraz spełnia równości:
ma trzeci stopień i wszystkie współczynniki całkowite oraz spełnia równości: 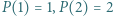 i
i 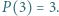 Wyznaczyć najmniejszą możliwą wartość
Wyznaczyć najmniejszą możliwą wartość 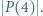
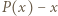 ma pierwiastki
ma pierwiastki 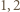 i
i 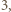 więc
więc 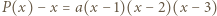 dla pewnego całkowitego
dla pewnego całkowitego 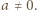
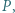 który ma czwarty stopień i spełnia równości:
który ma czwarty stopień i spełnia równości: 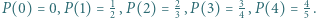
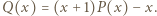 Jego pierwiastkami są
Jego pierwiastkami są 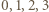 i
i 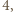 więc
więc 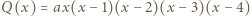 dla pewnego
dla pewnego 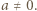 Liczba
Liczba 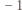 jest pierwiastkiem wielomianu
jest pierwiastkiem wielomianu 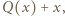 więc
więc 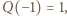 z czego wyznaczamy
z czego wyznaczamy 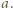
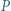 i
i 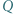 spełniają warunek
spełniają warunek 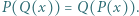 Wykazać, że wielomian
Wykazać, że wielomian 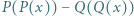 jest podzielny przez wielomian
jest podzielny przez wielomian 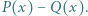
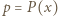 i
i 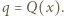 Mamy
Mamy 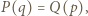 więc
więc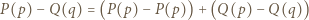
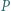 o współczynnikach całkowitych ma tę własność, że
o współczynnikach całkowitych ma tę własność, że 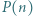 jest liczbą pierwszą dla wszystkich naturalnych
jest liczbą pierwszą dla wszystkich naturalnych 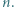 Dowieść, że
Dowieść, że 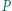 jest wielomianem stałym.
jest wielomianem stałym.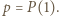 Na mocy twierdzenia
Na mocy twierdzenia 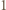 dla naturalnych
dla naturalnych 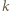 mamy
mamy 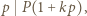 więc
więc 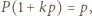 gdyż wartości
gdyż wartości 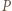 dla argumentów całkowitych są liczbami pierwszymi. Wielomian
dla argumentów całkowitych są liczbami pierwszymi. Wielomian 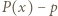 ma zatem nieskończenie wiele miejsc zerowych, więc jest zerowy.
ma zatem nieskończenie wiele miejsc zerowych, więc jest zerowy.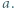 Niech
Niech 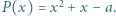 Udowodnić, że jeśli dla pewnego naturalnego
Udowodnić, że jeśli dla pewnego naturalnego 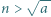 liczby
liczby 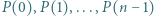 są względne pierwsze z
są względne pierwsze z 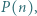 to liczba
to liczba 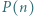 jest pierwsza.
jest pierwsza.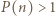 dla
dla 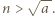 Przypuśćmy, że liczba
Przypuśćmy, że liczba 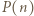 nie jest pierwsza. Wtedy ma ona dzielnik pierwszy
nie jest pierwsza. Wtedy ma ona dzielnik pierwszy 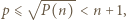 czyli
czyli 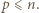 Wówczas
Wówczas 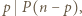 czyli
czyli 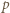 jest wspólnym dzielnikiem
jest wspólnym dzielnikiem 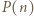 i
i 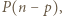 a to jest sprzeczne z założeniami.
a to jest sprzeczne z założeniami.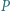 o współczynnikach całkowitych, spełniające warunek:
o współczynnikach całkowitych, spełniające warunek: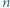 co najwyżej jedna z liczb
co najwyżej jedna z liczb 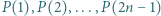 dzieli się przez
dzieli się przez 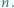
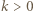 mamy
mamy 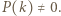 Niech
Niech 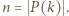 Ponieważ
Ponieważ 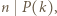 również
również 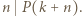 Zatem
Zatem 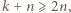 czyli
czyli 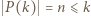 dla dużych
dla dużych 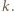 Stąd można wywnioskować, że
Stąd można wywnioskować, że 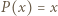 albo
albo 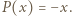
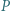 o współczynnikach całkowitych, które dla każdego naturalnego
o współczynnikach całkowitych, które dla każdego naturalnego 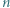 spełniają podzielność
spełniają podzielność 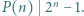
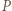 jest stały, to
jest stały, to 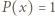 lub
lub 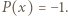 W przeciwnym razie dla pewnego
W przeciwnym razie dla pewnego 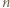 mamy
mamy 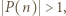 więc
więc 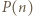 ma pewien dzielnik pierwszy
ma pewien dzielnik pierwszy 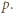 Mamy wtedy też
Mamy wtedy też 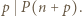 Zatem z założeń zadania
Zatem z założeń zadania 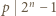 i
i 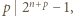 więc
więc 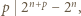 czyli
czyli 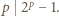 Jest to sprzeczne z małym twierdzeniem Fermata:
Jest to sprzeczne z małym twierdzeniem Fermata: 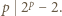
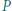 będzie wielomianem o współczynnikach wymiernych, który przyjmuje wartości niewymierne dla niewymiernych argumentów. Wykazać, że stopień
będzie wielomianem o współczynnikach wymiernych, który przyjmuje wartości niewymierne dla niewymiernych argumentów. Wykazać, że stopień 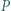 wynosi 1.
wynosi 1.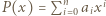 spełnia warunki zadania. Zauważmy, że możemy wybrać
spełnia warunki zadania. Zauważmy, że możemy wybrać 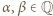 takie, że wielomian
takie, że wielomian 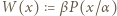 ma współczynniki całkowite oraz współczynnik przy najwyższej potędze wynosi 1. Niech
ma współczynniki całkowite oraz współczynnik przy najwyższej potędze wynosi 1. Niech 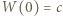 i niech
i niech 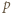 będzie liczbą pierwszą. Jeśli
będzie liczbą pierwszą. Jeśli 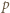 jest dostatecznie duże, to równanie
jest dostatecznie duże, to równanie 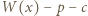 ma dokładnie jedno dodatnie rozwiązanie, które zgodnie z założeniem o wielomianie
ma dokładnie jedno dodatnie rozwiązanie, które zgodnie z założeniem o wielomianie 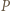 jest wymierne. Korzystając z twierdzenia o pierwiastkach wymiernych wielomianu o współczynnikach całkowitych dostajemy, że rozwiązaniem tym może być tylko
jest wymierne. Korzystając z twierdzenia o pierwiastkach wymiernych wielomianu o współczynnikach całkowitych dostajemy, że rozwiązaniem tym może być tylko 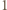 lub
lub 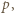 zatem dla dostatecznie dużych
zatem dla dostatecznie dużych 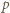 musi to być
musi to być 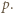 Wynika stąd, że
Wynika stąd, że 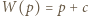 dla dostatecznie dużych liczb pierwszych
dla dostatecznie dużych liczb pierwszych 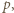 zatem
zatem 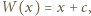 co oznacza, że
co oznacza, że 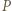 jest stopnia 1.
jest stopnia 1.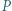 o współczynnikach całkowitych oraz względnie pierwsze dodatnie liczby całkowite
o współczynnikach całkowitych oraz względnie pierwsze dodatnie liczby całkowite 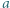 i
i 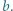 Udowodnić, że jeśli
Udowodnić, że jeśli 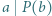 oraz
oraz 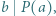 to
to 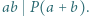
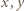 ma miejsce podzielność
ma miejsce podzielność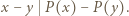
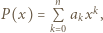 mamy
mamy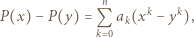
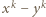 jest podzielna przez
jest podzielna przez 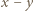 (w razie potrzeby przyjmujemy
(w razie potrzeby przyjmujemy 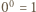 ).
).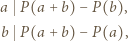
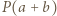 jest liczbą podzielną zarówno przez
jest liczbą podzielną zarówno przez 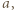 jak i przez
jak i przez 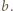 Pozostaje skorzystać z założenia, że liczby
Pozostaje skorzystać z założenia, że liczby 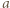 i
i 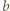 są względnie pierwsze.
są względnie pierwsze.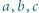 spełniają równości
spełniają równości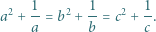
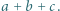
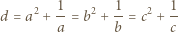
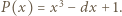 Skoro
Skoro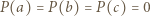
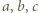 są różne, to są one różnymi pierwiastkami wielomianu
są różne, to są one różnymi pierwiastkami wielomianu 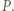 Stąd na mocy wzorów Viéte'a uzyskujemy
Stąd na mocy wzorów Viéte'a uzyskujemy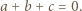
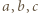 spełniające założenia zadania rzeczywiście istnieją, np.
spełniające założenia zadania rzeczywiście istnieją, np.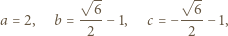
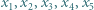 będą różnymi pierwiastkami wielomianu
będą różnymi pierwiastkami wielomianu 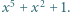 Wyznaczyć wartość wyrażenia
Wyznaczyć wartość wyrażenia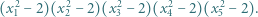
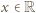
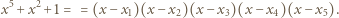
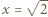 oraz
oraz 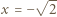 :
: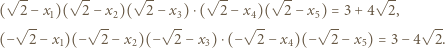
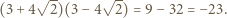
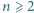 wyznaczyć taki wielomian
wyznaczyć taki wielomian 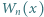 o współczynnikach wymiernych, że
o współczynnikach wymiernych, że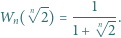
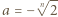 oraz
oraz 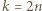 do tożsamości
do tożsamości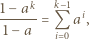
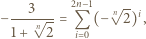
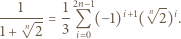
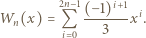
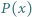 stopnia 2, o współczynnikach rzeczywistych, oraz liczba naturalna
stopnia 2, o współczynnikach rzeczywistych, oraz liczba naturalna 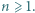 Udowodnić, że może istnieć co najwyżej jeden wielomian
Udowodnić, że może istnieć co najwyżej jeden wielomian 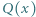 stopnia
stopnia 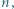 spełniający równanie
spełniający równanie 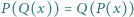 dla
dla 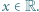
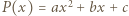
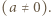 Przypuśćmy, że dla ustalonej liczby
Przypuśćmy, że dla ustalonej liczby 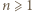 istnieją dwa różne wielomiany
istnieją dwa różne wielomiany 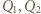 stopnia
stopnia 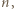 spełniające podane równanie. Oznaczmy ich współczynniki wiodące przez
spełniające podane równanie. Oznaczmy ich współczynniki wiodące przez 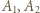 (więc
(więc 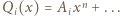 );
); 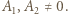 Przyrównując współczynniki wiodące po obu stronach równania
Przyrównując współczynniki wiodące po obu stronach równania 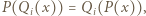 widzimy, że
widzimy, że 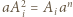 (dla
(dla 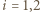 ). Zatem
). Zatem 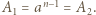 Stąd wynika, że różnica
Stąd wynika, że różnica 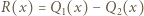 jest niezerowym wielomianem stopnia
jest niezerowym wielomianem stopnia 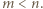
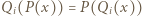 (dla
(dla 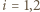 ) i przekształcamy uzyskaną równość:
) i przekształcamy uzyskaną równość: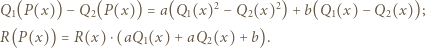
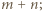 wielomian po lewej stronie ma stopień
wielomian po lewej stronie ma stopień 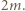 To już sprzeczność, skoro
To już sprzeczność, skoro 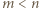 ; dwa różne wielomiany
; dwa różne wielomiany 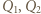 stopnia
stopnia 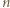 o podanej własności istnieć nie mogą.
o podanej własności istnieć nie mogą.