Wojnę powiedzieć myśli serce moje, Do której miecza nie trzeba ni zbroje»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu Wojnę powiedzieć myśli serce moje, Do której miecza nie trzeba ni zbroje
- Publikacja w Delcie: maj 2020
- Publikacja elektroniczna: 30 kwietnia 2020
Gracze stawiają pionki na szachownicy 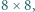 jeden czarne, a drugi białe. Żadne dwa pionki tego samego koloru nie mogą stać na polach mających wspólny bok lub wierzchołek. Przegrywa ten, kto nie może wykonać ruchu. Wskazać strategię wygrywającą.
jeden czarne, a drugi białe. Żadne dwa pionki tego samego koloru nie mogą stać na polach mających wspólny bok lub wierzchołek. Przegrywa ten, kto nie może wykonać ruchu. Wskazać strategię wygrywającą.
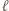 będzie osią symetrii szachownicy, równoległą do pewnych dwóch jej boków. Gracz drugi ma strategię wygrywającą - każdy swój pionek stawia symetrycznie do postawionego w poprzednim ruchu pionka przeciwnika względem prostej
będzie osią symetrii szachownicy, równoległą do pewnych dwóch jej boków. Gracz drugi ma strategię wygrywającą - każdy swój pionek stawia symetrycznie do postawionego w poprzednim ruchu pionka przeciwnika względem prostej 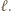
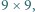 przy czym hetmana można postawić wyłącznie na wolnym polu, którego nie atakuje żaden z hetmanów ustawionych wcześniej. Przegrywa gracz, który nie może wykonać ruchu. Wskazać strategię wygrywającą.
przy czym hetmana można postawić wyłącznie na wolnym polu, którego nie atakuje żaden z hetmanów ustawionych wcześniej. Przegrywa gracz, który nie może wykonać ruchu. Wskazać strategię wygrywającą.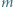 na
na 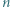 kostek. Dwaj gracze na zmianę łamią czekoladę wzdłuż linii prostej, nie uszkadzając kostek. Po złamaniu czekolady gracz wybiera jeden z dwóch otrzymanych kawałków i zjada go, a gra toczy się dalej na pozostałej części czekolady. Wygrywa ten, kto odda przeciwnikowi ostatnią kostkę. Wskazać strategię wygrywającą.
kostek. Dwaj gracze na zmianę łamią czekoladę wzdłuż linii prostej, nie uszkadzając kostek. Po złamaniu czekolady gracz wybiera jeden z dwóch otrzymanych kawałków i zjada go, a gra toczy się dalej na pozostałej części czekolady. Wygrywa ten, kto odda przeciwnikowi ostatnią kostkę. Wskazać strategię wygrywającą.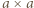 ) można otrzymać tylko z niekwadratowej. Zatem receptą na zwycięstwo jest tworzenie kwadratu, o ile to możliwe. Jeśli
) można otrzymać tylko z niekwadratowej. Zatem receptą na zwycięstwo jest tworzenie kwadratu, o ile to możliwe. Jeśli 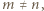 to zwycięży pierwszy gracz, a w przeciwnym razie - drugi.
to zwycięży pierwszy gracz, a w przeciwnym razie - drugi.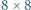 skoczki, przy czym gracz pierwszy stawia zawsze jednego, a gracz drugi trzy. Skoczki muszą stać na różnych polach i żadne dwa nie mogą się atakować. Przegrywa ten, kto nie może wykonać ruchu. Wskazać strategię wygrywającą.
skoczki, przy czym gracz pierwszy stawia zawsze jednego, a gracz drugi trzy. Skoczki muszą stać na różnych polach i żadne dwa nie mogą się atakować. Przegrywa ten, kto nie może wykonać ruchu. Wskazać strategię wygrywającą.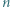 srebrnych i
srebrnych i 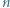 złotych. Ruch polega na zabraniu pewnej liczby monet z jednego lub dwóch stosów, ale złotych monet musi pozostać co najmniej tyle, co srebrnych. Ponadto, jeśli zabieramy monety z obu stosów, to po wykonaniu ruchu muszą one zawierać po tyle samo monet. Wygrywa gracz, który pozostawi na stole jedną złotą monetę i żadnej srebrnej. Wskazać strategię wygrywającą.
złotych. Ruch polega na zabraniu pewnej liczby monet z jednego lub dwóch stosów, ale złotych monet musi pozostać co najmniej tyle, co srebrnych. Ponadto, jeśli zabieramy monety z obu stosów, to po wykonaniu ruchu muszą one zawierać po tyle samo monet. Wygrywa gracz, który pozostawi na stole jedną złotą monetę i żadnej srebrnej. Wskazać strategię wygrywającą.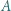 lub
lub 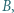 jedną na jeden ruch. Drugi może w swoim ruchu zamienić miejscami dowolne dwie litery napisanego słowa albo może nic nie zmieniać. Gra kończy się, gdy każdy z graczy wykona
jedną na jeden ruch. Drugi może w swoim ruchu zamienić miejscami dowolne dwie litery napisanego słowa albo może nic nie zmieniać. Gra kończy się, gdy każdy z graczy wykona 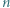 ruchów. Drugi gracz wygrywa, gdy powstałe słowo
ruchów. Drugi gracz wygrywa, gdy powstałe słowo 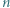 -literowe jest palindromem; w przeciwnym razie wygrywa pierwszy. Wskazać strategię wygrywającą.
-literowe jest palindromem; w przeciwnym razie wygrywa pierwszy. Wskazać strategię wygrywającą.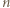 jest liczbą parzystą, to gracz pierwszy wygrywa, pisząc raz literę
jest liczbą parzystą, to gracz pierwszy wygrywa, pisząc raz literę 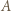 i
i 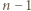 razy literę
razy literę 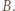 Gdy
Gdy 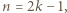 to wygrywa gracz drugi w następujący sposób. Przez pierwszych
to wygrywa gracz drugi w następujący sposób. Przez pierwszych 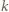 ruchów nie robi nic, a po napisaniu litery
ruchów nie robi nic, a po napisaniu litery 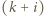 -tej sprawdza, czy jest ona taka sama jak
-tej sprawdza, czy jest ona taka sama jak 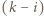 -ta. Jeśli tak, to nic nie robi, a jeśli nie, to literę
-ta. Jeśli tak, to nic nie robi, a jeśli nie, to literę 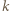 -tą zamienia z tą z liter
-tą zamienia z tą z liter 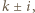 która jest od niej inna.
która jest od niej inna.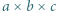 złożony jest z
złożony jest z 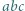 sześcianików o wymiarach
sześcianików o wymiarach 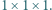 Ruch polega na przebiciu tego prostopadłościanu igłą na wylot, równolegle do wybranej krawędzi. W czasie ruchu zostaje przebitych
Ruch polega na przebiciu tego prostopadłościanu igłą na wylot, równolegle do wybranej krawędzi. W czasie ruchu zostaje przebitych 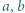 lub
lub  sześcianików. Żaden sześcianik nie może być przebity dwa razy, a przegrywa gracz, który jako pierwszy nie może wbić igły zgodnie z podanymi prawidłami. Wskazać strategię wygrywającą.
sześcianików. Żaden sześcianik nie może być przebity dwa razy, a przegrywa gracz, który jako pierwszy nie może wbić igły zgodnie z podanymi prawidłami. Wskazać strategię wygrywającą.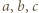 są parzyste, to wygrywa drugi gracz, wykonując ruchy środkowosymetryczne względem środka prostopadłościanu do ruchów gracza pierwszego. Jeśli są co najmniej dwie nieparzyste, powiedzmy
są parzyste, to wygrywa drugi gracz, wykonując ruchy środkowosymetryczne względem środka prostopadłościanu do ruchów gracza pierwszego. Jeśli są co najmniej dwie nieparzyste, powiedzmy 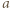 i
i 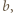 to strategię wygrywającą ma gracz pierwszy. Najpierw wbija igłę w środek ściany
to strategię wygrywającą ma gracz pierwszy. Najpierw wbija igłę w środek ściany 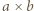 (ta igła przechodzi przez środek prostopadłościanu), a następnie odpowiada środkowosymetrycznie względem środka prostopadłościanu.
(ta igła przechodzi przez środek prostopadłościanu), a następnie odpowiada środkowosymetrycznie względem środka prostopadłościanu.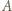 i
i 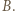 Pierwszą partię niech zaczyna
Pierwszą partię niech zaczyna 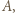 grając białymi. Po jego pierwszym ruchu przerwijmy na chwilę grę z nim i rozpocznijmy drugą partię, z
grając białymi. Po jego pierwszym ruchu przerwijmy na chwilę grę z nim i rozpocznijmy drugą partię, z 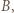 dokładnie tym samym ruchem, który
dokładnie tym samym ruchem, który 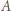 wykonał w pierwszej grze. Gracz
wykonał w pierwszej grze. Gracz 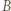 jakoś na ten ruch odpowie czarnymi. Wtedy wróćmy do przerwanej rozgrywki z
jakoś na ten ruch odpowie czarnymi. Wtedy wróćmy do przerwanej rozgrywki z 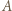 i powtórzmy w niej ten właśnie ruch czarnymi. I tak dalej, ruchy białymi gracza
i powtórzmy w niej ten właśnie ruch czarnymi. I tak dalej, ruchy białymi gracza 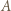 z pierwszej gry kopiujmy w grze drugiej, a ruchy
z pierwszej gry kopiujmy w grze drugiej, a ruchy 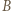 czarnymi z drugiej gry kopiujmy w grze pierwszej. W ten sposób dokładnie jedną z tych dwóch gier wygramy, czyli pokonamy arcymistrza szachowego (ewentualnie z obydwoma arcymistrzami zremisujemy - to też sukces!).
czarnymi z drugiej gry kopiujmy w grze pierwszej. W ten sposób dokładnie jedną z tych dwóch gier wygramy, czyli pokonamy arcymistrza szachowego (ewentualnie z obydwoma arcymistrzami zremisujemy - to też sukces!).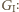 umieszcza pierwszą złotówkę na środku stolika, po czym na każdy ruch przeciwnika odpowiada, kładąc monetę symetrycznie względem środka. Jeśli
umieszcza pierwszą złotówkę na środku stolika, po czym na każdy ruch przeciwnika odpowiada, kładąc monetę symetrycznie względem środka. Jeśli 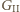 znalazł miejsce na monetę, to
znalazł miejsce na monetę, to 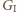 też znajdzie - miejsce symetryczne jest wolne.
też znajdzie - miejsce symetryczne jest wolne.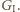 Może zacząć od narysowania jednej z głównych przekątnych i na każdy ruch przeciwnika odpowiadać ruchem symetrycznym względem niej.
Może zacząć od narysowania jednej z głównych przekątnych i na każdy ruch przeciwnika odpowiadać ruchem symetrycznym względem niej.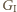 wygrywa nawet bez żadnej strategii, gdyż gra zawsze trwa 9 ruchów. Zauważ, że
wygrywa nawet bez żadnej strategii, gdyż gra zawsze trwa 9 ruchów. Zauważ, że 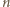 -kąt foremny ma
-kąt foremny ma 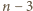 nieprzecinające się przekątne.
nieprzecinające się przekątne.
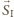 i
i 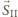 sumy wektorów wybranych przez graczy, a przez
sumy wektorów wybranych przez graczy, a przez 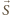 sumę danych wektorów:
sumę danych wektorów: 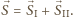 Jeśli
Jeśli 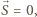 to gra kończy się remisem, bo
to gra kończy się remisem, bo 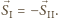 Jeśli
Jeśli 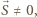 to wektory
to wektory 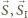 i
i 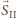 tworzą trójkąt - być może zdegenerowany. Stąd
tworzą trójkąt - być może zdegenerowany. Stąd 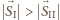 wtedy i tylko wtedy, gdy koniec wektora
wtedy i tylko wtedy, gdy koniec wektora 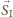 znajduje się po tej samej stronie symetralnej wektora
znajduje się po tej samej stronie symetralnej wektora 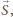 co koniec
co koniec 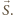 Strategią dla
Strategią dla 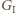 jest zatem maksymalizowanie składowej
jest zatem maksymalizowanie składowej 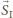 w kierunku
w kierunku 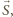 czyli spośród dostępnych wektorów branie zawsze takiego o największej składowej w kierunku
czyli spośród dostępnych wektorów branie zawsze takiego o największej składowej w kierunku 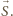 Wygrywa lub remisuje, bo
Wygrywa lub remisuje, bo 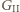 bierze zawsze wektor o co najwyżej równie dużej składowej w tym kierunku i łącznie ma tyle samo wektorów. Gdy gra jest remisowa, żadna inna strategia nie zagwarantowałaby
bierze zawsze wektor o co najwyżej równie dużej składowej w tym kierunku i łącznie ma tyle samo wektorów. Gdy gra jest remisowa, żadna inna strategia nie zagwarantowałaby 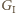 wygranej.
wygranej.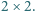

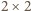 zawiera w całości pewną cegłę
zawiera w całości pewną cegłę 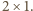 Jeśli
Jeśli 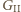 zawsze wstawia swój pionek, złośliwie, do tej samej cegły, w której właśnie zagrał
zawsze wstawia swój pionek, złośliwie, do tej samej cegły, w której właśnie zagrał 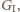 to
to 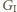 nie może wygrać. Jest to więc strategia nieprzegrywająca dla
nie może wygrać. Jest to więc strategia nieprzegrywająca dla 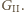 Pozostawiam Czytelnikom podobne sprawdzenie, że
Pozostawiam Czytelnikom podobne sprawdzenie, że 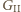 nie ma strategii wygrywającej.
nie ma strategii wygrywającej.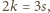 oraz wzór Eulera
oraz wzór Eulera 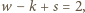 gdzie
gdzie 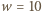 to liczba punktów planszy,
to liczba punktów planszy, 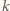 - liczba narysowanych odcinków, zaś
- liczba narysowanych odcinków, zaś  - liczba ścian (wliczając też ścianę zewnętrzną).
- liczba ścian (wliczając też ścianę zewnętrzną).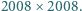 Dwaj gracze na przemian wykonują ruchy, z których każdy polega na wybraniu białego albo czarnego pionka i postawieniu go na wybranym wolnym polu. Wygrywa ten, którego ruch doprowadził do powstania ciągu 5 kolejnych pionków tego samego koloru w linii pionowej, poziomej lub ukośnej. Zbadaj, czy dla gracza rozpoczynającego grę istnieje strategia zapewniająca mu zwycięstwo.
Dwaj gracze na przemian wykonują ruchy, z których każdy polega na wybraniu białego albo czarnego pionka i postawieniu go na wybranym wolnym polu. Wygrywa ten, którego ruch doprowadził do powstania ciągu 5 kolejnych pionków tego samego koloru w linii pionowej, poziomej lub ukośnej. Zbadaj, czy dla gracza rozpoczynającego grę istnieje strategia zapewniająca mu zwycięstwo.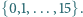 Mamy prawo zadać 7 pytań, oczekując odpowiedzi Tak lub Nie. Przeciwnik na wszystkie pytania odpowiada; wolno mu przy tym skłamać, ale co najwyżej jeden raz. Podać taktykę gwarantującą prawidłowe rozpoznanie wybranej liczby.
Mamy prawo zadać 7 pytań, oczekując odpowiedzi Tak lub Nie. Przeciwnik na wszystkie pytania odpowiada; wolno mu przy tym skłamać, ale co najwyżej jeden raz. Podać taktykę gwarantującą prawidłowe rozpoznanie wybranej liczby.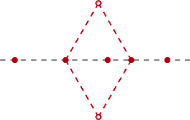
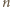 swoich ruchach Maja maluje na kolorowo
swoich ruchach Maja maluje na kolorowo 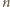 punktów z jednej prostej. Każdą parę takich kolorowych punktów można na dwa sposoby uzupełnić do trójkąta równobocznego, par punktów spośród
punktów z jednej prostej. Każdą parę takich kolorowych punktów można na dwa sposoby uzupełnić do trójkąta równobocznego, par punktów spośród  jest
jest 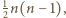 więc łącznie po
więc łącznie po 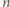 ruchach na płaszczyźnie jest
ruchach na płaszczyźnie jest 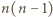 takich punktów, że pomalowanie dowolnego z nich na kolorowo da Mai zwycięstwo.
takich punktów, że pomalowanie dowolnego z nich na kolorowo da Mai zwycięstwo.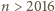 mamy
mamy 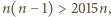 zatem Gucio nie może w swoich początkowych
zatem Gucio nie może w swoich początkowych 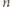 ruchach wszystkich opisanych powyżej punktów pomalować na czarno i Maja może wygrać w ruchu numer
ruchach wszystkich opisanych powyżej punktów pomalować na czarno i Maja może wygrać w ruchu numer 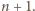
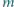 i
i  monetami. Ruch polega na usunięciu jednego ze stosów i podzieleniu drugiego na dwa niepuste. Gracze wykonują ruchy na przemian. Jeśli któryś nie może wykonać ruchu, to przegrywa. Rozstrzygnąć, kto ma strategię wygrywającą, gdy
monetami. Ruch polega na usunięciu jednego ze stosów i podzieleniu drugiego na dwa niepuste. Gracze wykonują ruchy na przemian. Jeśli któryś nie może wykonać ruchu, to przegrywa. Rozstrzygnąć, kto ma strategię wygrywającą, gdy 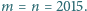
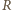 oznacza gracza rozpoczynającego, zaś
oznacza gracza rozpoczynającego, zaś 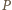 jego przeciwnika. Wykażemy, że
jego przeciwnika. Wykażemy, że 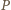 ma strategię wygrywającą, polegającą na pozostawianiu po każdym swoim ruchu dwóch stosów o nieparzystej liczbie monet.
ma strategię wygrywającą, polegającą na pozostawianiu po każdym swoim ruchu dwóch stosów o nieparzystej liczbie monet.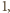 to
to 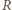 po wykonaniu swojego ruchu zostawi dla
po wykonaniu swojego ruchu zostawi dla 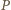 stos z parzystą liczbą monet (i drugi o nieparzystej liczbie monet). Wówczas
stos z parzystą liczbą monet (i drugi o nieparzystej liczbie monet). Wówczas 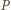 może usunąć stos o nieparzystej liczbie monet, a ten o parzystej liczbie monet podzielić na dwa stosy zgodnie ze swoją strategią.
może usunąć stos o nieparzystej liczbie monet, a ten o parzystej liczbie monet podzielić na dwa stosy zgodnie ze swoją strategią.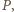 gdy zostawi on dla
gdy zostawi on dla 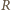 dwa jednomonetowe stosy.
dwa jednomonetowe stosy.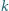 monetami. Gracz wykonujący ruch musi usunąć
monetami. Gracz wykonujący ruch musi usunąć 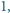
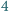 lub
lub 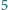 monet ze stosu. Gracze wykonują ruchy na przemian. Jeśli któryś nie może wykonać ruchu, to przegrywa. Rozstrzygnąć, kto ma strategię wygrywającą, gdy
monet ze stosu. Gracze wykonują ruchy na przemian. Jeśli któryś nie może wykonać ruchu, to przegrywa. Rozstrzygnąć, kto ma strategię wygrywającą, gdy 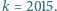
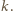 Niech
Niech 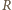 oznacza gracza rozpoczynającego, zaś
oznacza gracza rozpoczynającego, zaś 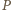 jego przeciwnika.
jego przeciwnika.
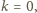 gracz rozpoczynający
gracz rozpoczynający 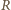 nie może wykonać ruchu, więc wygrywa jego przeciwnik - gracz
nie może wykonać ruchu, więc wygrywa jego przeciwnik - gracz 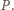
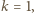 to
to 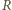 zabiera
zabiera 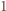 monetę i
monetę i 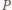 dostaje pusty stos i przegrywa.
dostaje pusty stos i przegrywa.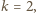 to
to 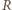 musi zabrać
musi zabrać 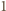 monetę i przeciwnik jest w przed chwilą przeanalizowanej wygrywającej sytuacji.
monetę i przeciwnik jest w przed chwilą przeanalizowanej wygrywającej sytuacji.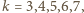 to
to 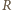 zabiera odpowiednio
zabiera odpowiednio 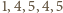 monet, zostawiając przeciwnika z
monet, zostawiając przeciwnika z 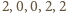 monetami, czyli
monetami, czyli 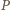 jest w przed chwilą przeanalizowanych pozycjach przegrywających.
jest w przed chwilą przeanalizowanych pozycjach przegrywających.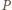 wygrywa wtedy i tylko wtedy, gdy
wygrywa wtedy i tylko wtedy, gdy 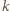 przystaje modulo 8 do 0 lub 2. Skoro
przystaje modulo 8 do 0 lub 2. Skoro 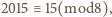 to
to 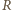 ma strategię wygrywającą.
ma strategię wygrywającą.