Kropki – kreski
W dzisiejszym świecie ludzie stają się coraz bardziej leniwi. Chcą osiągnąć zysk w krótkim czasie, bez zbytecznej pracy. Najłatwiejszym sposobem na „zarabianie” są gry. Ale czym właściwie jest gra?
W dzisiejszym świecie ludzie stają się coraz bardziej leniwi. Chcą osiągnąć zysk w krótkim czasie, bez zbytecznej pracy. Najłatwiejszym sposobem na „zarabianie” są gry. Ale czym właściwie jest gra?

Gry, zagadki, paradoksy Mała Delta
Legenda powiada, że gdy bóg Brahma po raz pierwszy poruszył czas, umieścił na jednej z trzech diamentowych igieł, umocowanych na wspólnej podstawce, 64 złote krążki. Na podstawce spoczywał krążek najszerszy, a nad nim lśniły pozostałe o coraz mniejszych średnicach. Bóg polecił mnichom z górskiej samotni, by bez spoczynku przekładali krążki, tak aby wszystkie znalazły się na drugiej diamentowej igle, z zachowaniem tego samego ułożenia. Gdy zadanie zostanie zakończone, nastąpi koniec pierwszego świata, a na następny, wskrzeszony przez Brahmę, wypadnie czekać wiele tysięcy lat...
Gry, zagadki, paradoksy Mała Delta
Wyobraźmy sobie następującą grę. Na stole w jednym rzędzie leży
 monet
o różnych nominałach. Dwoje graczy – Ania i Bartek – wykonuje na przemian ruchy,
zaczyna Ania. Ruch polega na zabraniu jednej monety z lewego lub prawego końca
rzędu. Wynikiem gry jest, oczywiście, suma nominałów monet zgromadzonych przez
każdego z graczy. Jak powinna grać Ania, by uzyskać jak największą sumę, jeśli wie
ona, że Bartek będzie grał optymalnie (tzn. będzie starał się zmaksymalizować swoją
sumę)?
monet
o różnych nominałach. Dwoje graczy – Ania i Bartek – wykonuje na przemian ruchy,
zaczyna Ania. Ruch polega na zabraniu jednej monety z lewego lub prawego końca
rzędu. Wynikiem gry jest, oczywiście, suma nominałów monet zgromadzonych przez
każdego z graczy. Jak powinna grać Ania, by uzyskać jak największą sumę, jeśli wie
ona, że Bartek będzie grał optymalnie (tzn. będzie starał się zmaksymalizować swoją
sumę)?
Przez świat przetoczyła się niedawno mania Sudoku i, co za tym idzie, wzrosło zainteresowanie tematem łamigłówek. W tym artykule przedstawię pewne matematyczne podejście do rozwiązywania łamigłówek, które wynika nie z samej struktury zadania, a jedynie z informacji, że ma ono jednoznaczne rozwiązanie.
Gry, zagadki, paradoksy Deltoid
Niektóre gry mogą wydawać się trudne, dopóki gracz się nie dowie, o co tak naprawdę w nich chodzi – wtedy nagle te same gry okazują się łatwe, czasem wręcz oczywiste...
Zastanówmy się nad pytaniem zawartym w tytule, to jest: czy partia szachów, przy bezbłędnej grze obu stron, zakończy się wygraną któregoś z graczy, czy może też nieunikniony jest remis? Do dziś nie jest znana odpowiedź na to pytanie i to pomimo faktu, że w rozwiązaniu tego problemu mogłyby nam pomóc odpowiednio napisany program i posłużenie się superkomputerem (a najlepiej mocą obliczeniową wielu takich urządzeń połączonych w jedną sieć – tak jak w przypadku globalnej sieci Internet).
Organizatorzy gier liczbowych typu lotto przeznaczają sporą część dochodu na zysk i koszt pozyskania dochodu i ten fakt sprawia, że wiele osób powstrzymuje się od gry, a dopiero mechanizm kumulacji powoduje zainteresowanie grą. Dla organizatorów gier kumulacja jest tylko formą odłożenia wypłaty, przeto nic na niej nie tracą, natomiast nowi grający, oczekujący zysku z podziału kwoty odłożonej, grają przeciw stałym graczom.
O ciekawych problemach związanych z kapeluszami pisaliśmy już w Delcie nie raz, ale że dobrego nigdy za wiele, napiszemy też i w tym numerze, tyle że inaczej.
Bolek i Lolek zdecydowali się zagrać w ryzykowną grę. Mają do dyspozycji czekoladę, podzieloną na małe kwadratowe kawałki. Nie jest to jednak zwyczajna czekolada – jej lewy dolny kwadrat jest zatruty. Ruch polega na wybraniu jednego niezjedzonego jeszcze kawałka oraz zjedzeniu go wraz ze wszystkimi znajdującymi się wyżej lub bardziej na prawo od niego (czyli podczas wykonywania ruchu trzeba zjeść przynajmniej jeden kawałek czekolady).
Gry, zagadki, paradoksy Stowarzyszenie na rzecz Edukacji Matematycznej
Z inicjatywy Stowarzyszenia na rzecz Edukacji Matematycznej oraz Instytutu Matematycznego PAN w zeszłym roku szkolnym zostało zorganizowane Olimpijskie Kółko Matematyczne przeznaczone przede wszystkim dla uczniów warszawskich liceów.
Rachunek prawdopodobieństwa Omega
W poprzednim numerze opisaliśmy prostą grę, w której trzeba było dokonać dwukrotnie właściwego wyboru jednej z dwóch możliwości, by zmaksymalizować średnią wygraną. Krótko mówiąc, był to dynamiczny problem decyzyjny. Zademonstrowaliśmy też trzy z wielu możliwych strategii, w tym optymalną (oczywiście lisa).

wikipedia
John Forbes Nash, Jr.
Zastosowania matematyki Nagrody Nobla
W 1762 roku Jean Jacques Rousseau napisał: „Polujący na jelenia myśliwi są w pełni świadomi, że aby go upolować, muszą być lojalni wobec siebie i pozostać na swoich posterunkach. Jeżeli jednak zając przebiegnie w pobliżu jednego z nich, nie ma wątpliwości, że myśliwy ten ruszy za pewną zdobyczą, doprowadzając do fiaska polowanie na jelenia.” Przetłumaczmy to na język współczesnej teorii gier...
Zastosowania matematyki Nagrody Nobla
W 2005 roku Nagrodę Nobla z ekonomii otrzymali za „przyczynienie się do zwiększenia naszego rozumienia mechanizmów konfliktu i kooperacji przez analizę teoriogrową” profesorowie Robert J. Aumann (Uniwersytet Hebrajski w Jerozolimie) oraz Thomas C. Schelling (Uniwersytet Maryland i Uniwersytet Harwarda).
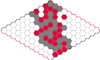
Gry, zagadki, paradoksy Wielkie granie
Hex jest jedną z najprostszych i jednocześnie jedną z najciekawszych z matematycznego
punktu widzenia gier planszowych. Rozgrywka heksa jest prowadzona na romboidalnej
planszy złożonej z sześciokątnych pól. Najbardziej typowe są plansze
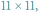 jak
na rysunku, ale można grać na dowolnie dużej planszy.
jak
na rysunku, ale można grać na dowolnie dużej planszy.
Gry, zagadki, paradoksy Mała Delta
W pewnym kraju żyło bardzo wielu mędrców. Któregoś dnia groźny król postanowił przekonać się, czy rzeczywiście zasługują oni na to zaszczytne miano i zapowiedział, że czeka ich trudna próba. Zebrał mędrców w swej komnacie i przedstawił im poniższe zasady.
Rachunek prawdopodobieństwa Omega
Czarownica
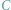 w punkcie
w punkcie
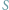 na rozstaju dróg mówi do lisa
na rozstaju dróg mówi do lisa
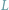 ,
wołu
,
wołu
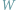 i konika polnego
i konika polnego
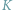 : „Pójdziesz w prawo, dostaniesz pół złotego,
...
: „Pójdziesz w prawo, dostaniesz pół złotego,
...
Piraci mają łup w postaci 100 dukatów i muszą go podzielić. Postanowili urządzić podział następująco...
W artykule „Gra w 20 pytań” omówiliśmy sposób gry z graczem, który nie kłamie. A jak postępować z graczem, który kłamie? Czy jesteśmy zupełnie bezradni?
Gry, zagadki, paradoksy Mała Delta
... to dobrze znana gra.