Klub 44M - zadania XII 2020»Zadanie 812
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania XII 2020
- Publikacja w Delcie: grudzień 2020
- Publikacja elektroniczna: 1 grudnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (421 KB)
-
Zadanie 812 zaproponował pan Tomasz Ordowski.
Udowodnić, że dla każdej liczby naturalnej 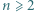 iloczyn
iloczyn 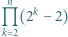 dzieli się przez
dzieli się przez 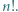
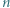
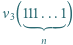
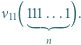
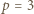 wystarczy rozważyć
wystarczy rozważyć 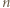 podzielne przez 3, a dla
podzielne przez 3, a dla 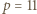 - rozważyć
- rozważyć  parzyste. Dla
parzyste. Dla 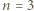 skorzystać z równości
skorzystać z równości 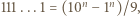 a dla
a dla 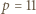 i
i 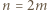 z równości
z równości 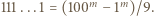
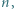
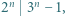
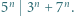
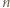 zachodzi nierówność
zachodzi nierówność 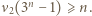 Wartość
Wartość 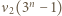 można wyznaczyć dokładnie, w zależności od parzystości
można wyznaczyć dokładnie, w zależności od parzystości 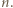 Skorzystać z nierówności
Skorzystać z nierówności 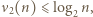 aby wykazać, że
aby wykazać, że 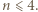
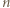 parzystych
parzystych 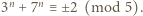 Dla
Dla 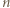 nieparzystych skorzystać z lematu w wersji z dodawaniem i postępować podobnie jak w podpunkcie (a).
nieparzystych skorzystać z lematu w wersji z dodawaniem i postępować podobnie jak w podpunkcie (a).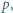
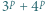
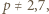 to
to 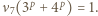
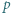 -adycznego w
-adycznego w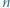
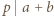 i
i 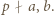 W przypadku
W przypadku 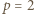 mamy
mamy 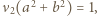 natomiast dla
natomiast dla 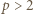 mamy
mamy 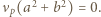
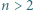
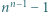
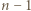 i stwierdzić, że
i stwierdzić, że 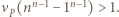

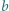
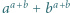
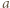 i
i 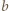 mają wspólny dzielnik pierwszy
mają wspólny dzielnik pierwszy 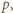 to
to 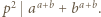 W przeciwnym razie istnieje liczba pierwsza
W przeciwnym razie istnieje liczba pierwsza 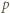 spełniająca warunki
spełniająca warunki 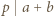 i
i 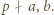 Wystarczy skorzystać z lematu w wersji z dodawaniem, rozumując podobnie jak w poprzednim zadaniu.
Wystarczy skorzystać z lematu w wersji z dodawaniem, rozumując podobnie jak w poprzednim zadaniu.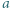
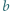
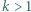
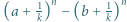
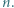
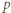 będzie dowolnym dzielnikiem pierwszym liczby
będzie dowolnym dzielnikiem pierwszym liczby 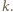 Jeśli liczba z zadania jest całkowita, to
Jeśli liczba z zadania jest całkowita, to 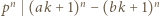 i można skorzystać z lematu, bo
i można skorzystać z lematu, bo 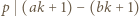 oraz
oraz 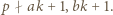
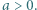
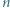
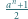
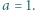
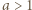 liczba
liczba 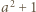 ma dzielnik pierwszy
ma dzielnik pierwszy 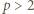 i dla odpowiednio dobranego nieparzystego
i dla odpowiednio dobranego nieparzystego 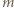 liczba
liczba 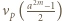 nie dzieli się przez 3.
nie dzieli się przez 3.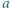
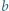
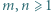
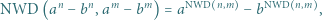
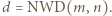 Stosując własności kongruencji, uzasadnić, że zbiór tych całkowitych
Stosując własności kongruencji, uzasadnić, że zbiór tych całkowitych 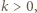 dla których
dla których 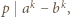 jest postaci
jest postaci 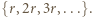
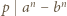 i
i 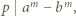 to
to 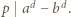
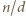 i
i 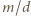
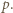 Wywnioskować z tego, że
Wywnioskować z tego, że 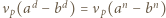 lub
lub 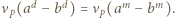
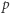 -adyczne
-adyczne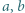
 :
:
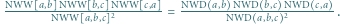
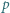
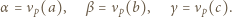
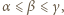
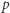 -adyczne
-adyczne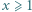
![|[x, 2x]](/math/temat/matematyka/teoria_liczb/zadania/2020/11/01/zm-20-11-kpo-2/2x-d7608384ddd380a3dd1f65eb0be5d8496d7a9363-im-2C,6B,73-FF,FF,FF.gif)
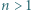 :
: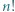
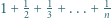
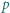
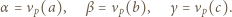
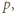
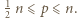
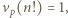
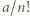
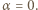
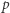 -adyczne
-adyczne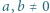
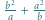
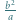
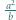
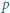
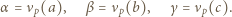
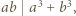
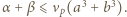
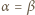
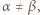
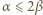
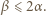
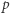 -adyczne
-adyczne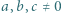
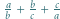
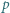
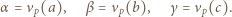
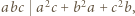
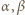
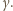
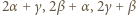
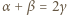
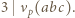
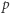 -adyczne
-adyczne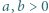
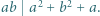

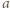
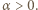

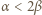
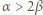
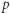 -adyczne
-adyczne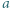
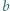
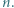
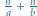
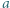
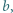
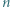
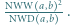
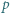
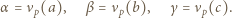
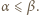
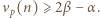
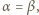
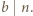
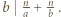
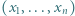
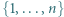
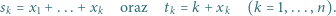
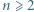
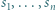

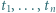
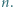
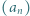 jest określony wzorami
jest określony wzorami 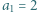 ;
; 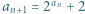 dla
dla 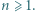 Niech
Niech 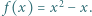 Udowodnić, że dla każdego
Udowodnić, że dla każdego 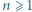 liczba
liczba 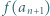 dzieli się przez
dzieli się przez 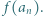
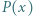 będzie wielomianem
będzie wielomianem 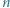 -tego stopnia
-tego stopnia 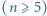 o współczynnikach całkowitych, mającym
o współczynnikach całkowitych, mającym 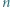 różnych pierwiastków całkowitych. Załóżmy, że 0 jest jednym z jego pierwiastków. Udowodnić, że wielomian
różnych pierwiastków całkowitych. Załóżmy, że 0 jest jednym z jego pierwiastków. Udowodnić, że wielomian 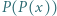 również ma dokładnie
również ma dokładnie  różnych pierwiastków całkowitych.
różnych pierwiastków całkowitych.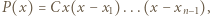 gdzie
gdzie 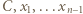 są liczbami całkowitymi. Oczywiście
są liczbami całkowitymi. Oczywiście 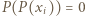 dla
dla 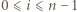 (przyjmujemy
(przyjmujemy 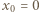 ). Załóżmy, że
). Załóżmy, że 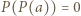 dla pewnego
dla pewnego 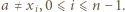 Wówczas
Wówczas 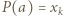 dla pewnego
dla pewnego 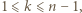 czyli
czyli 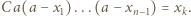 W tej sytuacji
W tej sytuacji 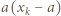 dzieli
dzieli 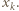 Załóżmy, że
Załóżmy, że 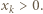 Z podzielności
Z podzielności 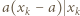 wnioskujemy kolejno
wnioskujemy kolejno 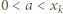 oraz
oraz 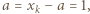 czyli
czyli 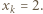 Jednak
Jednak 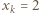 ma tylko 4 różne dzielniki całkowite, co przeczy równości
ma tylko 4 różne dzielniki całkowite, co przeczy równości 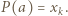 Przypadek
Przypadek 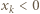 rozpatrujemy podobnie i w ten sposób kończymy dowód, że tylko pierwiastki wielomianu
rozpatrujemy podobnie i w ten sposób kończymy dowód, że tylko pierwiastki wielomianu 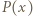 są całkowitymi pierwiastkami wielomianu
są całkowitymi pierwiastkami wielomianu 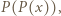 co dopełnia rozwiązanie.
co dopełnia rozwiązanie.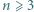 istnieją nieparzyste liczby
istnieją nieparzyste liczby 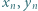 spełniające równanie
spełniające równanie 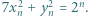
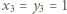 spełniają wymaganą w zadaniu równość. Załóżmy, że nieparzyste liczby
spełniają wymaganą w zadaniu równość. Załóżmy, że nieparzyste liczby 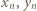 spełniają
spełniają 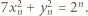 Wówczas
Wówczas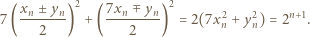
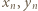 są nieparzyste, to jedna z par
są nieparzyste, to jedna z par 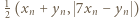 oraz
oraz 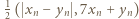 składa się z dwóch liczb nieparzystych, i tę parę wybieramy jako
składa się z dwóch liczb nieparzystych, i tę parę wybieramy jako 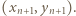 W ten indukcyjny sposób możemy skonstruować rozwiązanie wyjściowego równania dla dowolnej liczby naturalnej
W ten indukcyjny sposób możemy skonstruować rozwiązanie wyjściowego równania dla dowolnej liczby naturalnej