Jak wyciągnąć 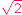 modulo
modulo 
Niech 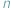 będzie liczbą nieparzystą...
będzie liczbą nieparzystą...
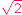 modulo
modulo 
Niech 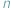 będzie liczbą nieparzystą...
będzie liczbą nieparzystą...

Pierre de Fermat (1601-1665)
Pierre de Fermat był Francuzem i żył w pierwszej połowie XVII wieku (1601-1665). Jako radca prawny praktykował w sądzie w Tuluzie na południu Francji. Naukami ścisłymi, a w szczególności matematyką, interesował się jako amator, ale wniósł potężny wkład do ich rozwoju. Szczególnie spektakularne są jego osiągnięcia w teorii liczb i o nich traktuje niniejszy artykuł. Wszyscy wiedzą, że jest Wielkie Twierdzenie Fermata (WTwF), Małe Twierdzenie Fermata (MTwF) i jeszcze inne twierdzenia Fermata dotyczące teorii liczb - ale które z nich jest największe?

Chaim Zelig Słonimski (1810-1904)
Przy dzieleniu liczb wielocyfrowych metodą pisemną często wykonuje się następującą operację...
Pierwszy etap pitagoreizmu głosił hasło wszystko jest liczbą: pożądaną Harmonię Świata da się wyrazić jako stosunek liczb (dziś nazywanych naturalnymi), przy czym jest ona tym pełniejsza, im liczby te są mniejsze.
Skończyłam! - krzyknęła triumfalnie Agatka do swojego brata, Bartka. Dziewczynka regularnie domaga się od starszego chłopca rozmaitych ciekawostek matematycznych, których ten dowiaduje się w liceum...
Słynne twierdzenie Dirichleta głosi, że jeżeli liczby naturalne 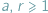 są względnie pierwsze, to ciąg arytmetyczny
są względnie pierwsze, to ciąg arytmetyczny 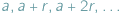 zawiera nieskończenie wiele liczb pierwszych. Przedstawimy kilka wniosków płynących z tego twierdzenia.
zawiera nieskończenie wiele liczb pierwszych. Przedstawimy kilka wniosków płynących z tego twierdzenia.
Wyobraźmy sobie, że trafiliśmy do dziwnego kraju, w którym jedynymi dostępnymi środkami płatniczymi są monety o nominałach 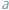 i
i 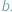 Formy płatności nie rozwinęły się na tyle, żeby płacić kartą lub czekiem, na domiar złego wybraliśmy się do cukierni, w której kasa jest zupełnie pusta i sprzedawca nie może wydać nam reszty. Nie chcąc tracić swoich złociaków, rozglądamy się za pysznościami w cenach
Formy płatności nie rozwinęły się na tyle, żeby płacić kartą lub czekiem, na domiar złego wybraliśmy się do cukierni, w której kasa jest zupełnie pusta i sprzedawca nie może wydać nam reszty. Nie chcąc tracić swoich złociaków, rozglądamy się za pysznościami w cenach 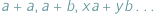 Niektórych kwot, oczywiście, nie daje się uzyskać z nominałów
Niektórych kwot, oczywiście, nie daje się uzyskać z nominałów 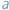 i
i  a niektóre można otrzymać na wiele sposobów.
a niektóre można otrzymać na wiele sposobów.
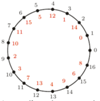
Na obrazku widać przenumerowanie szesnastu z 17 równo rozmieszczonych punktów na okręgu. Obok "normalnych" czarnych numerków podano dziwnie rozmieszczone czerwone. Zrobiono to w ten sposób, że nawinięto na ten okrąg półprostą, na której zaznaczono punkty odpowiadające kolejnym potęgom 3.
W 1994 roku Peter Shor, pracujący wówczas w Bell Labs w New Jersey, pokazał, jak przy użyciu hipotetycznego komputera kwantowego rozłożyć w czasie wielomianowym dowolną liczbę naturalną na czynniki pierwsze. W tamtym czasie algorytmy kwantowe dopiero raczkowały. To właśnie odkrycie Shora spowodowało wielki rozwój tej dziedziny. Społeczność informatyków zrozumiała, że gdyby udało się zbudować komputer kwantowy rozsądnej wielkości, to świat stałby się istotnie inny. Nie jest bowiem znany żaden algorytm dla problemu faktoryzacji, czyli rozkładu na dzielniki pierwsze, który działa w czasie wielomianowym na komputerze klasycznym. Co więcej, nawet nie znaleziono algorytmu losowego, który z dużym prawdopodobieństwem w zazwyczaj niedługim czasie faktoryzuje liczbę: nie jest po prostu znana zupełnie żadna rozsądna heurystyka...
W Delcie 7/2017 przedstawiliśmy kilka "olimpijskich" zastosowań twierdzenia Combinatorial Nullstellensatz. Okazuje się, że zamiast "zwykłych" wielomianów wielu zmiennych możemy rozważać wielomiany o współczynnikach będących resztami z dzielenia przez pewną liczbę pierwszą 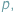 z dodawaniem i mnożeniem modulo
z dodawaniem i mnożeniem modulo 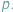 Poniżej przedstawimy trzy klasyczne twierdzenia, których proste dowody są oparte na Combinatorial Nullstellensatz w wersji "resztowej". Twierdzenia te są szczególnie bliskie zastosowaniom olimpijskim.
Poniżej przedstawimy trzy klasyczne twierdzenia, których proste dowody są oparte na Combinatorial Nullstellensatz w wersji "resztowej". Twierdzenia te są szczególnie bliskie zastosowaniom olimpijskim.
O trudnym problemie, który ma jednozdaniowe rozwiązanie...
Kiedy miałem kilka, kilkanaście lat, wraz ze starszym bratem często graliśmy w grę. Należało w swojej kolejce podać liczbę większą od wskazanej przez poprzednika. Przegrywał oczywiście ten, kto nie był w stanie podać liczby większej. Czasami ponosiła nas fantazja i mówiliśmy "nieskończoność" albo "nieskończoność plus nieskończoność". Dziś już wiem, że nieskończoność liczbą nie jest, a działania na nieskończonościach są bardziej wyrafinowane, niż podejrzewałem. Gdyby i Tobie, drogi Czytelniku, przyszło kiedyś wymienić (albo usłyszeć) jakąś dużą liczbę, możesz sięgnąć do poniższej listy. Nie są to bowiem byle jakie liczby...
W historii ludzkiego poznania mało jest tak fascynujących pojęć jak liczby pierwsze. Chociaż dzisiaj wiemy o nich znacznie więcej niż 120 lat temu, to jeszcze więcej dotyczących ich pytań pozostaje bez odpowiedzi. Celem tej notki jest pokazanie, że trudno jest ocenić na pierwszy rzut oka, czy pytanie dotyczące liczb pierwszych jest łatwe, czy też bardzo trudne - poza zasięgiem współczesnej nauki.
W tym artykule chcemy zaprezentować pewną technikę dowodową zwaną interpretacją kombinatoryczną. Metoda ta pokazana będzie w działaniu: podajemy dwa zadania wraz z rozwiązaniami, które są ilustracją tematu.
Małe Twierdzenie Fermata ma również taki dowód...
Dawno, dawno temu, za drugą górą, za trzecią rzeką żył sobie królewicz Leonardo pochodzący ze szlachetnego rodu Fibonaccich. No, może nie całkiem królewicz, ale piąty syn dyplomaty włoskiego. Może nie całkiem za trzecią rzeką, bo urodził się za ósmą doliną i trzynastoma bagnami, dokładniej w Pizie w 1175 roku. Zatem przynajmniej rzeczywiście żył dawno, dawno temu. Choć w pewnym sensie żyje do dzisiaj w swoich uczniach, bowiem wieść o liczbach Fibonacciego rozeszła się po świecie i szumi o nich niejeden las...
Artykuł o powyższym tytule wypada rozpocząć od przypomnienia, czym są kongruencje. Jeśli dwie liczby naturalne 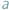 i
i 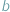 dają tę samą resztę z dzielenia przez liczbę naturalną
dają tę samą resztę z dzielenia przez liczbę naturalną 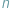 (innymi słowy, jeśli
(innymi słowy, jeśli  jest podzielne przez
jest podzielne przez 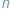 ), uczenie jest stwierdzić, że
), uczenie jest stwierdzić, że 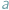 i
i 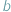 przystają do siebie modulo
przystają do siebie modulo 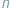 i fakt ten zanotować jako
i fakt ten zanotować jako 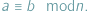 W tym kontekście znaczek "
W tym kontekście znaczek "  " (lub raczej to, co on sobą reprezentuje) nazywamy właśnie kongruencją.
" (lub raczej to, co on sobą reprezentuje) nazywamy właśnie kongruencją.
Jakie jest największe miasto na świecie? Czy wirus jest organizmem żywym? Jaki jest najpiękniejszy obraz Tycjana? Są to proste pytania, na które nie ma jednoznacznej odpowiedzi. Przyczyną jest brak jasno określonych kryteriów. Jedną z cech wyróżniających matematykę spośród innych dziedzin życia i nauki jest to, że każde pojęcie ma swoją precyzyjną definicję. Wydaje się więc, że na każde pytanie matematyczne jest jednoznaczna odpowiedź, którą można formalnie uzasadnić. W konsekwencji, nic nie jest brane "na wiarę". Okazuje się, że nie do końca tak jest!
Tak zwana zasada szufladkowa Dirichleta, jakże lubiana przez rozmaite komitety olimpiad matematycznych, łączy w sobie dwie atrakcyjne cechy. Z jednej strony jest tak prosta, że nawet dziecko w przedszkolu jest w stanie ją zrozumieć, z drugiej zaś zawiera zupełnie nieoczywisty element niekonstruktywny. Głosi ona mianowicie, że wkładając do 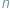 szuflad więcej niż
szuflad więcej niż 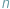 przedmiotów, mamy pewność, że w którejś szufladzie będą co najmniej dwa obiekty. W której - nie wiadomo, ale na pewno w którejś.
przedmiotów, mamy pewność, że w którejś szufladzie będą co najmniej dwa obiekty. W której - nie wiadomo, ale na pewno w którejś.