ZM-20.12-KPO-1»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu
Lemat o zwiększaniu wykładnika p-adycznego
- Publikacja w Delcie: grudzień 2020
- Publikacja elektroniczna: 1 grudnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (465 KB)
W zależności od 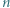 wyznaczyć
wyznaczyć 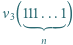 i
i 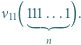
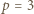 wystarczy rozważyć
wystarczy rozważyć 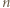 podzielne przez 3, a dla
podzielne przez 3, a dla 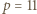 - rozważyć
- rozważyć  parzyste. Dla
parzyste. Dla 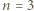 skorzystać z równości
skorzystać z równości 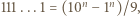 a dla
a dla 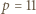 i
i 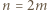 z równości
z równości 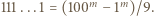
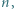
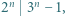
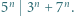
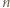 zachodzi nierówność
zachodzi nierówność 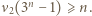 Wartość
Wartość 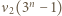 można wyznaczyć dokładnie, w zależności od parzystości
można wyznaczyć dokładnie, w zależności od parzystości 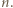 Skorzystać z nierówności
Skorzystać z nierówności 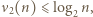 aby wykazać, że
aby wykazać, że 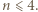
 parzystych
parzystych  Dla
Dla 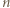 nieparzystych skorzystać z lematu w wersji z dodawaniem i postępować podobnie jak w podpunkcie (a).
nieparzystych skorzystać z lematu w wersji z dodawaniem i postępować podobnie jak w podpunkcie (a).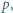
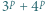
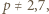 to
to 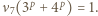
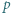 -adycznego w
-adycznego w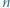
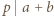 i
i 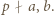 W przypadku
W przypadku 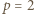 mamy
mamy 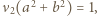 natomiast dla
natomiast dla 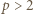 mamy
mamy 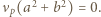
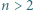
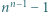
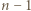 i stwierdzić, że
i stwierdzić, że 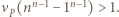

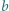
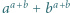
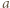 i
i 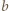 mają wspólny dzielnik pierwszy
mają wspólny dzielnik pierwszy 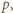 to
to 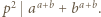 W przeciwnym razie istnieje liczba pierwsza
W przeciwnym razie istnieje liczba pierwsza 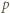 spełniająca warunki
spełniająca warunki 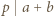 i
i 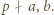 Wystarczy skorzystać z lematu w wersji z dodawaniem, rozumując podobnie jak w poprzednim zadaniu.
Wystarczy skorzystać z lematu w wersji z dodawaniem, rozumując podobnie jak w poprzednim zadaniu.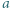
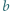
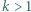
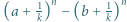
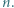
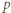 będzie dowolnym dzielnikiem pierwszym liczby
będzie dowolnym dzielnikiem pierwszym liczby 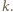 Jeśli liczba z zadania jest całkowita, to
Jeśli liczba z zadania jest całkowita, to 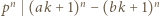 i można skorzystać z lematu, bo
i można skorzystać z lematu, bo 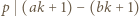 oraz
oraz 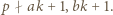
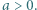
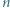
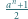
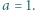
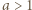 liczba
liczba 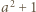 ma dzielnik pierwszy
ma dzielnik pierwszy 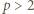 i dla odpowiednio dobranego nieparzystego
i dla odpowiednio dobranego nieparzystego 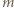 liczba
liczba 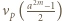 nie dzieli się przez 3.
nie dzieli się przez 3.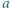
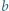
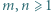
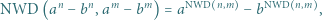
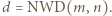 Stosując własności kongruencji, uzasadnić, że zbiór tych całkowitych
Stosując własności kongruencji, uzasadnić, że zbiór tych całkowitych 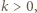 dla których
dla których 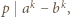 jest postaci
jest postaci 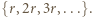
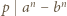 i
i 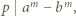 to
to 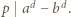
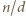 i
i 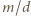
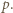 Wywnioskować z tego, że
Wywnioskować z tego, że 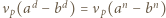 lub
lub 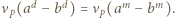
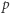 -adyczne
-adyczne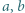
 :
:
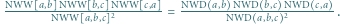
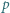
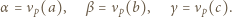
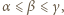
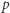 -adyczne
-adyczne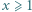
![|[x, 2x]](/math/temat/matematyka/teoria_liczb/zadania/2020/11/01/zm-20-11-kpo-2/2x-d7608384ddd380a3dd1f65eb0be5d8496d7a9363-im-2C,6B,73-FF,FF,FF.gif)
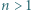 :
: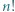
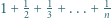
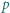
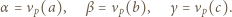
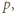
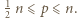
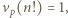
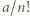
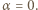
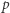 -adyczne
-adyczne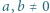
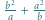
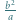
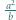
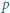
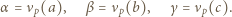
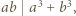
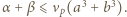
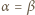
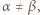
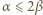
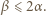
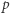 -adyczne
-adyczne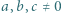
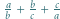
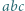
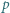
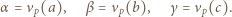
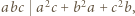
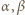
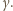
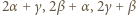
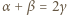
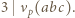
 -adyczne
-adyczne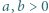
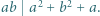

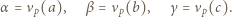
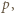
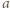
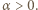

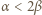
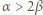
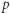 -adyczne
-adyczne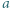
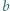
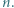
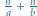
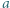
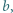
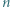
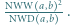
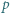
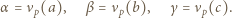
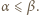
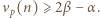
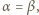
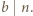
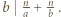
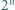 jedynek ma co najmniej
jedynek ma co najmniej 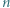 różnych dzielników pierwszych.
różnych dzielników pierwszych.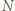 będzie liczbą składającą się w zapisie dziesiętnym z
będzie liczbą składającą się w zapisie dziesiętnym z 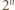 jedynek. Mamy
jedynek. Mamy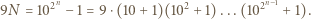
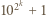 i
i 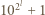 są względnie pierwsze dla
są względnie pierwsze dla 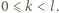 Załóżmy, że obie te liczby są podzielne przez liczbę pierwszą
Załóżmy, że obie te liczby są podzielne przez liczbę pierwszą 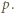 Oczywiście liczba
Oczywiście liczba 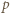 jest nieparzysta. Ponieważ
jest nieparzysta. Ponieważ 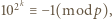 więc
więc 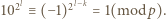 Skoro jednak
Skoro jednak 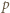 dzieli
dzieli 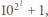 to
to 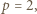 co przeczy wcześniej poczynionej uwadze o nieparzystości
co przeczy wcześniej poczynionej uwadze o nieparzystości 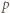 i kończy rozwiązanie zadania.
i kończy rozwiązanie zadania.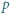

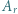
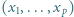
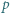 ), że
), że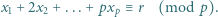
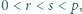

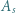
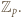
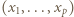


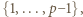
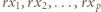
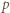
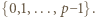
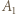 - czyli spełniała zależność
- czyli spełniała zależność 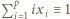 (mod
(mod 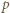 ) - to po pomnożeniu wszystkich jej wyrazów przez
) - to po pomnożeniu wszystkich jej wyrazów przez 
 - czyli permutację należącą do zbioru
- czyli permutację należącą do zbioru 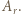
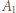
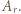
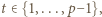
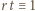 (mod
(mod 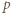 ) (taki element
) (taki element 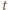
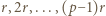
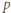
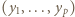
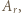
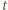
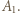
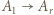 (mnożenie przez
(mnożenie przez  ) oraz
) oraz 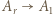 (mnożenie przez
(mnożenie przez 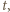
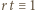 ) są wzajemnie odwrotne. To dowodzi, że zbiór
) są wzajemnie odwrotne. To dowodzi, że zbiór 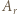
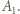
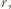
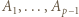
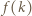 dla
dla 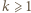 będzie liczbą liczb pierwszych w zbiorze
będzie liczbą liczb pierwszych w zbiorze 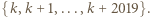 Wśród pierwszych 2020 liczb całkowitych dodatnich jest więcej niż 13 liczb pierwszych, zatem
Wśród pierwszych 2020 liczb całkowitych dodatnich jest więcej niż 13 liczb pierwszych, zatem 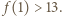 Zauważmy także, że wśród liczb
Zauważmy także, że wśród liczb 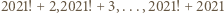 występują same liczby złożone, zatem
występują same liczby złożone, zatem 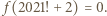 Oczywiście mamy
Oczywiście mamy 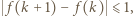 skąd wniosek, że istnieje taka liczba
skąd wniosek, że istnieje taka liczba 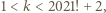 dla której mamy
dla której mamy 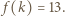 To kończy rozwiązanie zadania.
To kończy rozwiązanie zadania.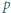 będzie liczbą pierwszą większą od 2. Udowodnić, że istnieje dokładnie jeden sposób przedstawienia
będzie liczbą pierwszą większą od 2. Udowodnić, że istnieje dokładnie jeden sposób przedstawienia 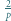 w postaci sumy
w postaci sumy 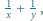 gdzie
gdzie 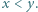
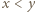 spełniają
spełniają 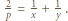 Równanie to można sprowadzić do postaci
Równanie to można sprowadzić do postaci 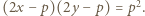 Ponieważ
Ponieważ 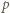 jest liczbą pierwszą, wynika stąd, że
jest liczbą pierwszą, wynika stąd, że 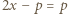 lub
lub 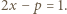 Pierwsza z tych możliwości oznaczałaby, że
Pierwsza z tych możliwości oznaczałaby, że 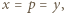 co przeczy zależności
co przeczy zależności 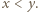 Musi być zatem
Musi być zatem 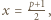 skąd
skąd 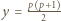 ; ponieważ
; ponieważ 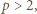 liczby te są całkowite i faktycznie spełniają wymaganą równość.
liczby te są całkowite i faktycznie spełniają wymaganą równość.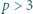 oraz takie liczby całkowite dodatnie
oraz takie liczby całkowite dodatnie 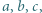 że
że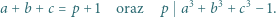
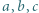 jest równa 1.
jest równa 1.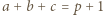 i
i 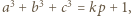 gdzie
gdzie 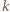 jest jakąś liczbą całkowitą. Wywnioskować stąd, że
jest jakąś liczbą całkowitą. Wywnioskować stąd, że 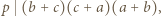 więc któryś z czynników dzieli się przez
więc któryś z czynników dzieli się przez 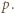 Te czynniki są dodatnie i nie przekraczają
Te czynniki są dodatnie i nie przekraczają 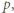 więc któryś z nich jest równy
więc któryś z nich jest równy