Delta mi!

Ile wierzchołków, krawędzi, ścian dwuwymiarowych, trójwymiarowych etc. ma -wymiarowy sześcian?

Dwunastościan wielki jest jednym z czterech niewypukłych wielościanów foremnych. Jego ścianami są przenikające się pięciokąty foremne (pentagony). Oczywiście, jest ich dwanaście. I w tym przypadku jest w miarę prosty sposób rysowania.

W Delcie była już mowa o ruchomych wielościanach, nazywanych też fleksorami; artykuły o nich ukazały się w 1987 i 1997 roku. Ruchomość wielościanu polega na tym, że gdybyśmy zbudowali model o sztywnych ścianach, a krawędziach poruszających się jak zawiasy, to moglibyśmy nim poruszać bez odkształcania ścian. Choć wydaje się to zaskakujące, ruchome wielościany rzeczywiście istnieją i zbudowanie takich brył, choćby z papieru, nie jest bardzo trudne.

wunastościan gwiaździsty mały wygląda bardzo ładnie, jakby ktoś dokleił odpowiednie piramidy do dwunastościanu foremnego. Jego ścianami są pięciokąty gwiaździste przenikające się i, jak sugeruje nazwa, powinno ich być 12. Czy da się to narysować? Naturalnie, przecież rysunek to skończony ciąg kresek...

W tym kąciku chcielibyśmy powrócić do pewnych własności sfery wpisanej w czworościan, o których pisaliśmy w kąciku 2 o najmocniejszym twierdzeniu stereometrii (Delta 3/2010). Okazuje się, że można je wykorzystać do udowodnienia faktów pozornie niezwiązanych ze sferą wpisaną.

Dwunastościan rombowy jest figurą o zadziwiających własnościach. Narysowanie go nie powinno sprawiać większych trudności. Jak nazwa wskazuje, ścianami tego dwunastościanu są romby, zatem rysunek zaczynamy od narysowania właśnie rombu.

Tym razem opowiemy o punkcie Fermata–Torricellego w czworościanie...

Ostatnio rysowaliśmy dwunastościan foremny i dwudziestościan foremny. Przedstawimy jeszcze jeden sposób rysowania dwunastościanu foremnego.

Dla trójkąta definiujemy okrąg opisany i okrąg wpisany. Podobnie z czworościanem można związać dwie naturalne sfery: sferę przechodzącą przez wierzchołki (opisaną) oraz sferę styczną do ścian (wpisaną). Można jednak rozważać jeszcze trzecią ciekawą sferę – styczną do krawędzi.

Narysujemy teraz figurę bardziej skomplikowaną: dwudziestościan...

W wielu rysunkach bardzo pomocny jest sześcian, z narysowaniem którego raczej nie mamy problemu...

Kontynuujemy opowieść o czworościanach równościennych – tym razem przyjrzymy się paru zadaniom z nimi związanym. Jakiś czas temu na konkursach matematycznych temat tych wdzięcznych czworościanów był dosyć modny...

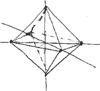
Kontynuujemy lekcje rysunku rozpoczęte w Delcie 6/2012. Kolejnym obiektem, który będziemy rysować, jest ośmiościan.

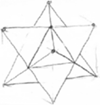
Wydaje się, że w czasach szybkich komputerów, programów graficznych i innych gadżetów nie ma sensu zajmowanie się rysunkiem odręcznym. Równie dobrze jednak można by zrezygnować z nauki pisania i tabliczki mnożenia – są przecież odpowiednie edytory i kalkulatory. Zdarza się jednak, że rozwiązując jakieś zadanie, dobrze byłoby podeprzeć naszą wyobraźnię właśnie rysunkiem, a nie ma pod ręką supernowoczesnych narzędzi.

W zawodach I stopnia obecnej, LXIII Olimpiady Matematycznej wzięło udział 1409 uczniów, więc nieco mniej niż w poprzedniej. Jest to liczba bliska wieloletniej średniej. Do drugiego stopnia zakwalifikowano 622 uczniów. Zawody drugiego stopnia odbyły się 17 i 18 lutego.

Czy istnieje czworościan który nie jest foremny, a którego ściany są trójkątami przystającymi? Istnieje...

Na płaszczyźnie, jeśli trójkąt ma równe boki, to jest równoboczny. W przestrzeni jednak czworościan, którego ściany są przystające, wcale nie musi być foremny...

Czasem przydaje się do czegoś twierdzenie o dwusiecznej...

Każdy, kto był w dżungli lub chociaż widział ją w jakimś filmie, wie, że poruszanie się po niej jest, delikatnie mówiąc, dosyć uciążliwe. Stanowi to ogromny kłopot szczególnie wtedy, gdy ktoś się w niej zgubi i chce się jakoś wydostać. Nie dość, że nie wiadomo, w jakim kierunku iść, to w ogóle ciężko jest nam pokonywać przeszkody (a rozwiązania siłowe, takie jak maczeta, niewiele dają). Istnieje następujące zalecenie: wystarczy znaleźć strumień (co zresztą wcale nie musi być łatwe), a potem liczyć na to, że zaprowadzi nas on do większej rzeki, a ta, być może, do morza.

W tym kąciku zajmiemy się pewnym zadaniem o czworościanie foremnym, o którym, między innymi, miałem okazję opowiadać na XLVI Szkole Matematyki Poglądowej pod hasłem Podejście niestandardowe.