Delta mi!

Święta za pasem, więc przygotujmy się nieco do wieszania bombek na choince.

W tym odcinku przyjrzymy się kątom dwuściennym. Jedną z najbardziej skutecznych metod radzenia sobie z nimi jest przeformułowanie problemu tak, żeby zamiast kątów dwuściennych pojawiły się kąty płaskie.

Na pierwszym etapie tegorocznej Olimpiady Matematycznej pojawiło się poniższe zadanie 1 o numerowaniu krawędzi dwunastościanu. Spośród licznych zadań o podobnej tematyce prezentujemy kilka o dość różnorodnych rozwiązaniach.

W dniu 8 stycznia 2011 roku odbyły się zawody II stopnia VI Olimpiady Matematycznej Gimnazjalistów, w których uczestniczyło 669 uczniów. Spośród nich 187 zostało zakwalifikowanych do zawodów stopnia III.

Dla każdej liczby naturalnej 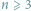można, oczywiście, narysować wielokąt, który ma 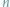 boków. A jak to będzie z wielościanami o zadanej z góry liczbie krawędzi?

Czasami, gdy zbytnio bujamy w obłokach, słyszymy od innych zejdź na ziemię! Kto by pomyślał, że ta zazwyczaj dość nieprzyjemna uwaga może być niekiedy cenną wskazówką do zadań ze stereometrii.

Pytanie postawione w tytule wydaje się dziwne. Przecież wiadomo co najmniej od czasów Platona, że wielościanów foremnych jest pięć typów: czworościan foremny, sześcian oraz ośmiościan, dwunastościan i dwudziestościan – wszystkie foremne. Łatwo też pokazuje się, że nie może być ich więcej. W czym zatem problem?

Polski namiot na francuskim Festiwalu Nauki był tak pełen gości, że miejsce dla jego matematycznej części życzliwie zostało ofiarowane przez Jeana Brette’a i jego kolegów w namiocie Pałacu Odkryć.

Tym razem, zgodnie z obietnicą, kącik poświęcimy czworościanom ortocentrycznym. Jak wiadomo, nie w każdym czworościanie istnieje punkt przecięcia wszystkich wysokości. Czworościany mające taki punkt nazywane są ortocentrycznymi. Spróbujmy opisać je dokładniej.