Stereometria Nowości z przeszłości
Jeszcze raz o wzorze Eulera, czyli zastosowanie stawów i grobli w stereometrii
W 1752 roku znakomity matematyk szwajcarski Euler, podówczas profesor Akademii Nauk w Berlinie, odkrył zadziwiający związek między liczbami 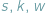 ścian, krawędzi i wierzchołków dowolnego wielościanu wypukłego
ścian, krawędzi i wierzchołków dowolnego wielościanu wypukłego 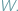 Związek ten jest obecnie nazywany wzorem Eulera dla wielościanów i zwykle zapisuje się go w postaci
Związek ten jest obecnie nazywany wzorem Eulera dla wielościanów i zwykle zapisuje się go w postaci

Podamy elementarny i chyba nader zabawny dowód tego wzoru.
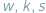 liczby odpowiednio wierzchołków, krawędzi i ścian wielościanu. W każdym wierzchołku schodzą się co najmniej trzy końce krawędzi i każda krawędź ma dwa końce, zatem
liczby odpowiednio wierzchołków, krawędzi i ścian wielościanu. W każdym wierzchołku schodzą się co najmniej trzy końce krawędzi i każda krawędź ma dwa końce, zatem 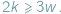 Podobnie każda ściana ma co najmniej trzy boki, a każda krawędź należy do dwóch ścian, więc
Podobnie każda ściana ma co najmniej trzy boki, a każda krawędź należy do dwóch ścian, więc 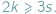 Ponadto jeśli wielościan jest wypukły, zachodzi wzór Eulera:
Ponadto jeśli wielościan jest wypukły, zachodzi wzór Eulera: 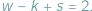

 i doklejeniu do drugiej części (czekającej w tym czasie w bezruchu). Szczęśliwa całość - sferostożek (ang. sphericon).
i doklejeniu do drugiej części (czekającej w tym czasie w bezruchu). Szczęśliwa całość - sferostożek (ang. sphericon).