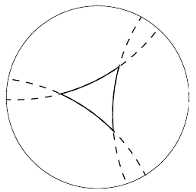
Jaki jest kształt Wszechświata?
W stosunku do wielkości Ziemi wszystkie ziemskie nierówności (łańcuchy górskie, doliny) to znikome, zaniedbywalne zniekształcenia. Ponieważ w naszej skali nasze bliskie otoczenie przypomina płaską powierzchnię, więc nie powinno nas dziwić, że pierwsze geometryczne rozważania dotyczyły płaszczyzny.
Kulminacją geometrycznych osiągnięć antycznego świata są Elementy Euklidesa napisane w III wieku p.n.e. Euklides wykazał, jak można na płaszczyźnie użyć pięciu aksjomatów do systematycznego wywnioskowania z nich dużego zbioru twierdzeń geometrycznych. Oto aksjomaty Euklidesa:
- I.
- Od dowolnego punktu do dowolnego punktu można poprowadzić prostą.
- II.
- Ograniczoną prostą można w sposób ciągły przedłużyć do prostej.
- III.
- Z dowolnego środka dowolnym promieniem można zakreślić okrąg.
- IV.
- Wszystkie kąty proste są równe.
- V.
- Jeśli prosta padająca na dwie proste tworzy po jednej stronie kąty wewnętrzne w sumie mniejsze od dwóch kątów prostych, to te dwie proste przedłużone nieskończenie przetną się po tej stronie (Rys. 1).
Piąty aksjomat Euklidesa ma także następujące sformułowanie (John Playfair, 1785 r.).
- V'.
- Przez każdy punkt poza prostą przechodzi dokładnie jedna prosta z nią rozłączna.
Jako przykład wykorzystania aksjomatów uzasadnimy dobrze znaną na płaszczyźnie obserwację: suma miar kątów trójkąta równa się 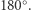
W pierwszym kroku wykażemy, że jeśli prosta 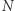 przecina dwie proste równoległe
przecina dwie proste równoległe 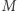 i
i 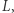 to naprzemianległe kąty są równe (Rys. 2). Z aksjomatu V
to naprzemianległe kąty są równe (Rys. 2). Z aksjomatu V 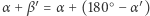 musi być równe
musi być równe 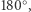 bo w przeciwnym wypadku proste
bo w przeciwnym wypadku proste 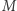 i
i 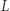 przecinają się. Stąd
przecinają się. Stąd 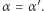 Analogicznie
Analogicznie 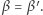
Niech będzie dany trójkąt 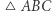 o kątach
o kątach 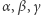 (Rys. 3). Wobec II aksjomatu prostą łączącą
(Rys. 3). Wobec II aksjomatu prostą łączącą 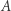 i
i 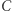 możemy przedłużyć do prostej
możemy przedłużyć do prostej 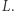 Z aksjomatu V' (postulatu o równoległych) istnieje prosta
Z aksjomatu V' (postulatu o równoległych) istnieje prosta 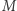 przechodząca przez punkt
przechodząca przez punkt 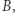 która nie przecina prostej
która nie przecina prostej 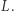 Wówczas z dowiedzionej już części
Wówczas z dowiedzionej już części 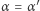 i
i 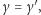 więc
więc 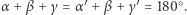
Najwięcej kontrowersji budził V aksjomat Euklidesa. Przez stulecia próbowano wywnioskować go z czterech pozostałych aksjomatów. I choć próby te kończyły się niepowodzeniem (na końcu artykułu przedstawiamy kilka z nich), to nikt nie był pewien, czy jakiś młody geniusz za sto czy dwieście lat nie będzie miał wspaniałego nowego pomysłu, który w końcu doprowadzi do poszukiwanego dowodu. Gdyby udało się stworzyć taki model geometrii, w którym pierwsze cztery aksjomaty byłyby prawdziwe, a V aksjomat nie byłby spełniony, to sprawa byłaby definitywnie wyjaśniona - V aksjomat byłby niezależny od czterech pozostałych. Ten problem okazał się trudny. Czy gdzieś istnieją trójkąty o sumie miar kątów nie dających 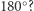 Jeszcze w XVIII wieku Immanuel Kant w Krytyce czystego rozumu (1781 r.) głosił, że geometria euklidesowa jest wiedzą a priori - jest nam dana wraz z życiem. Kant się mylił!
Jeszcze w XVIII wieku Immanuel Kant w Krytyce czystego rozumu (1781 r.) głosił, że geometria euklidesowa jest wiedzą a priori - jest nam dana wraz z życiem. Kant się mylił!
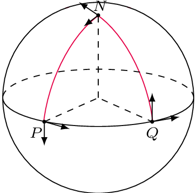
Dalekie podróże skłaniały ludzi do zastanawiania się nad tym, czy Ziemia jest płaska? Jak to rozstrzygnąć, pozostając stale na Ziemi? Obserwacje zaćmień Księżyca i cienia, jaki pozostawia na nim Ziemia, nie są przekonujące. Postąpimy inaczej, z bieguna północnego 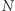 idziemy do równika
idziemy do równika 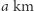 do punktu
do punktu 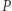 (Rys. 4). Na równiku skręcamy pod kątem prostym na wschód i idziemy wzdłuż równika
(Rys. 4). Na równiku skręcamy pod kątem prostym na wschód i idziemy wzdłuż równika 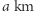 do punktu
do punktu 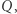 po czym pod kątem prostym skręcamy na północ i po
po czym pod kątem prostym skręcamy na północ i po 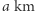 znajdujemy się na biegunie
znajdujemy się na biegunie 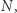 gdzie wektor kierunku naszego marszu jest teraz prostopadły do wektora kierunku naszego startu. Okazało się, że w ten sposób wytyczyliśmy na Ziemi trójkąt
gdzie wektor kierunku naszego marszu jest teraz prostopadły do wektora kierunku naszego startu. Okazało się, że w ten sposób wytyczyliśmy na Ziemi trójkąt 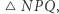 którego suma miar kątów jest równa
którego suma miar kątów jest równa 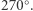 O takiej powierzchni (na której sumy miar kątów w trójkącie przekraczają
O takiej powierzchni (na której sumy miar kątów w trójkącie przekraczają 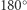 ) mówimy, że ma krzywiznę dodatnią. Zatem Ziemia nie jest płaska!
) mówimy, że ma krzywiznę dodatnią. Zatem Ziemia nie jest płaska!
Jak na takiej powierzchni (sferze) zachowują się aksjomaty Euklidesa? Aby odpowiedzieć na to pytanie, musimy określić na tej powierzchni pojęcie prostej. Na płaszczyźnie prosta łącząca punkty 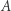 i
i 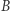 charakteryzuje się tym, że jest najkrótszą ścieżką łączącą te punkty. Gdy punkty
charakteryzuje się tym, że jest najkrótszą ścieżką łączącą te punkty. Gdy punkty 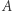 i
i 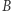 umieścimy na sferze, to najkrótszym odcinkiem je łączącym będzie krótszy fragment koła wielkiego, który powstanie z przecięcia sfery przez płaszczyznę, jaką wyznaczają punkty
umieścimy na sferze, to najkrótszym odcinkiem je łączącym będzie krótszy fragment koła wielkiego, który powstanie z przecięcia sfery przez płaszczyznę, jaką wyznaczają punkty 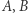 i środek sfery. Na przykład najkrótsza droga łącząca Paryż i Vancouver przebiega przez okolice bieguna północnego.
i środek sfery. Na przykład najkrótsza droga łącząca Paryż i Vancouver przebiega przez okolice bieguna północnego.
Skoro prostymi na sferze są koła wielkie, to łatwo widać, że na sferze V aksjomat Euklidesa jest fałszywy. Niech 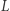 będzie równikiem Ziemi i
będzie równikiem Ziemi i 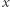 punktem na półkuli północnej. Jakiekolwiek koło wielkie przechodzące przez punkt
punktem na półkuli północnej. Jakiekolwiek koło wielkie przechodzące przez punkt 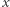 będzie w połowie leżeć na półkuli północnej, a w połowie na półkuli południowej, przecinając równik w dwóch (!) antypodycznych punktach (Rys. 5). Innymi słowy, na Ziemi nie ma prostej przechodzącej przez punkt
będzie w połowie leżeć na półkuli północnej, a w połowie na półkuli południowej, przecinając równik w dwóch (!) antypodycznych punktach (Rys. 5). Innymi słowy, na Ziemi nie ma prostej przechodzącej przez punkt 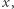 która nie przecina prostej
która nie przecina prostej 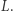 Niestety ten model geometrii (zwany geometrią sferyczną) nie pozwala na rozstrzygnięcie, czy V aksjomat jest niezależny od czterech pozostałych aksjomatów. Powód jest trywialny. Nie wszystkie pierwsze cztery aksjomaty Euklidesa są prawdziwe w geometrii sferycznej. Na przykład sfera nie zawiera okręgów o dowolnie dużym promieniu (aksjomat III), punkty antypodyczne (biegun północny i południowy) łączy nieskończenie wiele prostych, a na płaszczyźnie przez dwa różne punkty przechodzi dokładnie jedna prosta (podważa to I aksjomat).
Niestety ten model geometrii (zwany geometrią sferyczną) nie pozwala na rozstrzygnięcie, czy V aksjomat jest niezależny od czterech pozostałych aksjomatów. Powód jest trywialny. Nie wszystkie pierwsze cztery aksjomaty Euklidesa są prawdziwe w geometrii sferycznej. Na przykład sfera nie zawiera okręgów o dowolnie dużym promieniu (aksjomat III), punkty antypodyczne (biegun północny i południowy) łączy nieskończenie wiele prostych, a na płaszczyźnie przez dwa różne punkty przechodzi dokładnie jedna prosta (podważa to I aksjomat).
Potrzebujemy innej geometrii. Z listów Gaussa wynika, że około 1817 roku uświadomił on sobie, że można zbudować logicznie spójną geometrię, różną od euklidesowej (z odrzuconym V aksjomatem), ale swoich przemyśleń nie ogłosił. Zrobili to niezależnie od siebie Nikołaj Łobaczewski (1829 r.) i János Bolyai (1832 r.).
Rys. 7. Podział dysku hiperbolicznego za pomocą pięciokątów. Wyróżniony gwiazdką pięciokąt ma boki takiej samej długości jak pięciokąt centralny i takie samo pole
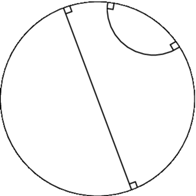
Na rysunku 6 przedstawiamy model dwuwymiarowej geometrii hiperbolicznej odkryty przez Eugenio Beltramiego w 1868 roku (14 lat później podał go również Henri Poincaré). Zrozumienie tego modelu wymaga nie tylko zdefiniowania linii prostej, ale również obowiązującej w nim odległości. W tym modelu przestrzeń jest przedstawiona jako wnętrze koła (bez brzegu). Prostymi są średnice lub łuki okręgów euklidesowych przecinające brzeg koła pod kątem prostym (Rys. 6). Proste są wyznaczone jednoznacznie przez dwa punkty lub przez punkt i koniec, lub przez dwa końce. Odległości stają się większe (w porównaniu do tego, jak wyglądają), gdy zbliżamy się do brzegu tak, że brzeg jest nieskończenie daleko od centrum. W rezultacie najkrótsza droga między dwoma punktami ma tendencję do odchylania się w kierunku centrum i, jak już mówiliśmy, jest łukiem okręgu euklidesowego, który przecina brzeg pod kątem prostym (Rys. 7).
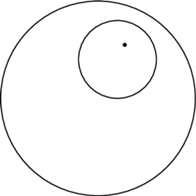
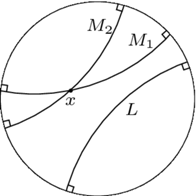
Dodatkowo w tym modelu koła są zawsze reprezentowane przez koła euklidesowe, ale mają przesunięte środki (Rys. 8), ich promienie mogą być dowolnie duże, wówczas koło prawie dotyka brzegu modelu. Kąty, w tym "prostopadłość", są w tym modelu wiernie przeniesione z płaszczyzny euklidesowej. Oznacza to, że w takiej przestrzeni spełnione są wszystkie pierwsze cztery aksjomaty Euklidesa. A co z V aksjomatem? Otóż w modelu geometrii hiperbolicznej V aksjomat Euklidesa jest fałszywy, co widać na rysunku 9. Proste 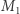 i
i 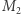 przecinają się w punkcie
przecinają się w punkcie 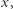 ale żadna z nich nie przecina prostej
ale żadna z nich nie przecina prostej 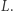 Zatem w modelu geometrii hiperbolicznej istnieją dwie proste przechodzące przez punkt
Zatem w modelu geometrii hiperbolicznej istnieją dwie proste przechodzące przez punkt  (tak naprawdę nieskończenie wiele), które nie przecinają prostej
(tak naprawdę nieskończenie wiele), które nie przecinają prostej 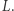 Pokazaliśmy w ten sposób, że Euklides miał rację, przyjmując V aksjomat, gdyż jest on niezależny od czterech pozostałych aksjomatów! Teraz już wiemy, że wszelkie próby wyprowadzenia V aksjomatu Euklidesa z czterech pozostałych aksjomatów z góry były skazane na niepowodzenie.
Pokazaliśmy w ten sposób, że Euklides miał rację, przyjmując V aksjomat, gdyż jest on niezależny od czterech pozostałych aksjomatów! Teraz już wiemy, że wszelkie próby wyprowadzenia V aksjomatu Euklidesa z czterech pozostałych aksjomatów z góry były skazane na niepowodzenie.
Ponadto w geometrii hiperbolicznej suma miar kątów trójkąta jest mniejsza niż 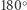 (Rys. 10). O takiej powierzchni mówimy, że ma krzywiznę ujemną.
(Rys. 10). O takiej powierzchni mówimy, że ma krzywiznę ujemną.
W ten oto sposób odkryliśmy, że istnieją różne geometrie i żadna z nich nie jest bardziej uprzywilejowana od innych. 10 czerwca 1854 roku Bernhard Riemann, mając 28 lat, w swoim wykładzie habilitacyjnym O hipotezach, które leżą u podstaw geometrii poszedł jeszcze dalej. Umieszczając obserwatora wewnątrz przestrzeni (wielowymiarowej rozmaitości), stwierdził, że geometria przestrzeni może się zmieniać od punktu do punktu, tu być hiperboliczną, tam euklidesową, a gdzie indziej sferyczną.
Próby dowodu V aksjomatu Euklidesa:
- (1)
- Niech
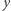 będzie innym punktem po tej samej stronie prostej
będzie innym punktem po tej samej stronie prostej 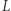 co punkt
co punkt  i w tej samej od niej odległości. Połącz
i w tej samej od niej odległości. Połącz 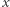 z
z 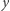 prostą (I aksjomat), a następnie przedłuż tę ograniczoną prostą do prostej
prostą (I aksjomat), a następnie przedłuż tę ograniczoną prostą do prostej 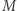 (II aksjomat). Wtedy prosta
(II aksjomat). Wtedy prosta 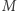 nie przecina prostej
nie przecina prostej 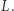
- (2)
- Niech prosta
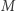 będzie złożona ze wszystkich punktów po tej samej stronie prostej
będzie złożona ze wszystkich punktów po tej samej stronie prostej 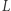 co punkt
co punkt  i będących od niej w tej samej odległości. Otrzymana prosta nie przecina prostej
i będących od niej w tej samej odległości. Otrzymana prosta nie przecina prostej 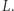
- (3)
- Punkt na płaszczyźnie kartezjańskiej można zapisać za pomocą współrzędnych. Prosta (nie pionowa)
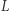 ma równanie
ma równanie 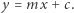 Zmieniając
Zmieniając 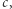 możemy przesunąć prostą
możemy przesunąć prostą 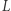 w górę lub w dół. Żadna z tak otrzymanych prostych nie może się przecinać i każdy punkt należy do dokładnie jednej prostej.
w górę lub w dół. Żadna z tak otrzymanych prostych nie może się przecinać i każdy punkt należy do dokładnie jednej prostej.
Dzisiaj za sprawą ogólnej teorii względności Alberta Einsteina (1916 r.) i potwierdzającej ją obserwacji Arthura Eddingtona z roku 1919 przyjmujemy, że otaczająca nas przestrzeń (dokładniej czasoprzestrzeń) jest zakrzywiona, choć możliwe, że tego typu zakrzywienia są tylko niewielkimi perturbacjami znacznie większego i bardziej symetrycznego kształtu.
Tytułowe pytanie o kształt Wszechświata jest jednym z wielkich otwartych problemów astronomii (kosmologii) - czy wielkoskalowy kształt Wszechświata, gdyby wyprostować łuki, ugięcia wynikające z obecności gwiazd, galaktyk, czarnych dziur itp., nadal byłby zakrzywiony jak wielka kula, czy też byłby płaski (jak wodne łóżko), a może jest on bardziej skomplikowaną wielowymiarową rozmaitością o ujemnej krzywiźnie. Może Ty masz pomysł, jak to rozstrzygnąć, Czytelniku?