Wyobraźmy sobie, że rysujemy krawędzie wielościanu na przezroczystej sferze, następnie przykładamy oko do tej sfery. To, co widzimy, nazywa się rzutem stereograficznym.

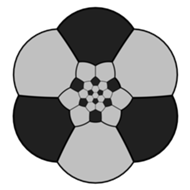
Spójrzmy na klasyczną piłkę nożną. Jest ona wielościanem, którego ścianami jest 12 czarnych pięciokątów i 20 białych sześciokątów. W każdym wierzchołku stykają się dwa białe sześciokąty i jeden czarny pięciokąt. Na rysunku obok piłka nożna przedstawiona jest w rzucie stereograficznym. Co by było, gdybyśmy zastąpili pięciokąt inną figurą?

W tej piłce pięciokąt można zastąpić kwadratem lub trójkątem. Chcąc stworzyć taki wielościan z papieru, można wyciąć wszystkie potrzebne białe i czarne ściany, a następnie odpowiednio je połączyć. Ta metoda wymaga jednak dużo wycinania i klejenia, czego możemy sobie oszczędzić, tworząc siatkę docelowego wielościanu (czyli niektóre ze ścian od razu będą połączone). Taki wielościan można przedstawić jak na rysunku obok, pamiętając o tym, że jedna ze ścian (ta, przez którą patrzymy do wewnątrz sfery) nie jest na nim przedstawiona. Gdy będziemy tworzyć siatkę zgodnie z zasadami, że dwie białe i jedna czarna figura mają spotkać się w każdym wierzchołku, to otrzymamy właśnie tę bryłę, o którą nam chodziło.

Gdy będziemy chcieli w piłce nożnej zamienić pięciokąty na sześciokąty, to łatwo się zorientujemy, że nie istnieje wielościan, którego ścianami są same sześciokąty. Oczywiście można wykonać konstrukcję z papieru, otrzymamy wtedy coś takiego jak obok.

Pójdźmy dalej i zamieńmy czarne figury na siedmiokąty.

Przed rozpoczęciem sklejania warto rozrysować na kartce strukturę czegoś takiego. Wynik przedstawiony jest na rysunku obok. Podobnie jak w przypadku czarnych sześciokątów, nasza konstrukcja nie będzie się składała w wielościan. Nie będzie się także składała w płaszczyznę. Da się ją jednak wykonać, jeśli ograniczymy się na przykład do 50 figur w odległości co najwyżej 3 od środkowego siedmiokąta. Konstrukcja siatki jest trochę trudniejsza niż w przypadku wielościanów. Jeden czarny sześciokąt i 2 białe idealnie mieściły się wokół wierzchołka, natomiast 1 czarny pięciokąt i 2 białe sześciokąty nie tylko się mieściły, ale także zostawiały trochę miejsca (które należało wyciąć i skleić). Tutaj czarny siedmiokąt i 2 białe sześciokąty już się nie mieszczą. Nie jest to jednak dużym problemem, blok techniczny jest na tyle giętki, by lekko wyginając papier dało się taką konstrukcję wykonać, i jednocześnie na tyle sztywny, by zachowywała ona swój kształt. Taką atrakcyjną konstrukcję niestety dosyć trudno przedstawić na dwuwymiarowych zdjęciach czy filmach - lepiej pobawić się samemu. Pora wyjaśnić, co to właściwie jest.

Kiedy w "piłce" czarne były sześciokąty, to otrzymaliśmy płaszczyznę. Dwudziestościan przycięty (z czarnymi pięciokątami) przypomina kulę - co widać na przykładzie piłki nożnej. Wersje z kwadratami i trójkątami również przypominają kulę, ale już nie tak dobrze. Nasza siedmiokątna konstrukcja również przybliża pewną powierzchnię.

Przykładowa gotowa siatka konstrukcji z siedmiokątami znajduje się tutaj. Polecamy wydrukować na czterech kartkach A4. Do szybkiego i mocnego "sklejania" można użyć zszywacza.

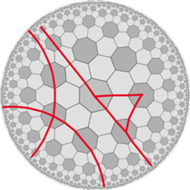
Nasze rysunki przedstawiają płaszczyznę hiperboliczną w modelu Poincaré, który jest odpowiednikiem rzutu stereograficznego sfery. W tym modelu cała płaszczyzna hiperboliczna mieści się w dysku, proste przedstawione są jako łuki okręgów lub odcinki przecinające brzeg dysku pod kątem prostym.

Jakie własności ma ta powierzchnia? By to zbadać, spróbujmy rysować na niej linie proste - jako że mamy tylko przybliżenie, nie możemy prostych rysować gdziekolwiek. Jeśli zaczniemy w środku siedmiokąta i narysujemy linię prostą w kierunku wierzchołka lub środka krawędzi, to jest dosyć jasne, jak będziemy musieli ją kontynuować. Dla łatwiejszego zrozumienia, na rysunku obok rysujemy odcinki, używając naszej dwuwymiarowej reprezentacji. Z trzech odcinków łączących środki trzech najbliżej leżących siedmiokątów możemy stworzyć trójkąt i obliczyć sumę jego kątów: 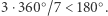Możemy też narysować prostą, nazwijmy ją 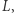i jakiś punkt poza nią. Okaże się, że przez ten punkt można poprowadzić różne proste nieprzecinające 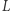- można to zrobić na kilka znacząco różnych sposobów. Z tego wynika, że ta powierzchnia różni się od płaszczyzny, gdzie suma kątów w trójkącie wynosi 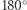i przez punkt poza prostą 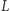można przeprowadzić tylko jedną prostą do niej równoległą. Ta powierzchnia różni się także znacząco od sfery, gdzie suma kątów w trójkącie jest zawsze większa niż 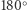i proste równoległe nie istnieją - równoleżniki nie są prostymi.

Geometria przybliżana przez konstrukcję z siedmiokątami jest nazywana geometrią hiperboliczną, a jej odkrycie jest jednym z najciekawszych, najbardziej zaskakujących fragmentów historii matematyki. Spełnia ona wszystkie postulaty geometrii Euklidesa oprócz piątego. Euklides, podobnie jak wielu innych matematyków przez 2000 lat, wierzył, że piąty postulat da się wyprowadzić z pozostałych. Nasza konstrukcja jest dowodem, że nie da się tego zrobić.

Wyobraźmy sobie, że spacerujemy po takiej konstrukcji i w każdym kroku możemy przejść na nowe pole, o ile ma ono wspólną krawędź z tym, na którym obecnie się znajdujemy. Można obliczyć, że liczba figur w odległości co najwyżej 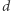kroków od wybranego siedmiokąta zależy wykładniczo od 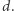Jako że wartości funkcji postaci 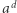są zawsze od pewnego momentu większe niż 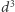(czy dowolny inny wielomian zmiennej 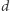), nie jest możliwe włożenie całej płaszczyzny hiperbolicznej w przestrzeń euklidesową - po prostu 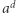figur nie mieści się w kuli o promieniu 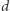w przestrzeni trójwymiarowej, przynajmniej jeśli robimy model z papieru (Hilbert wykazał, że nie można tego zrobić również z abstrakcyjną płaszczyzną hiperboliczną).

Zachęcam do wirtualnego spaceru po płaszczyźnie hiperbolicznej, którego można doświadczyć w grze HyperRogue - gra toczy się na opisanej powyżej siatce z sześciokątów i siedmiokątów. Gra ma także opcję tworzenia gotowej do wycięcia siatki opisanego w artykule modelu (na podstawie sceny z gry) oraz możliwość tworzenia trójwymiarowego komputerowego modelu tej powierzchni.