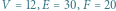O trójkątach na sferze
Znany jest wzór na sumę kątów w trójkącie:
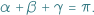 |
Dotyczy on oczywiście trójkątów na płaszczyźnie. Jaki związek ma płaskość (lub zakrzywienie) z powyższym wzorem? O tym za chwilę.

Rys. 1. Trójkąt o trzech kątach prostych
Pójdźmy krok dalej i rozważmy trójkąty geodezyjne na sferze. Są to obszary wycięte ze sfery za pomocą trzech płaszczyzn przechodzących przez środek sfery. Dzięki temu wierzchołki takiego trójkąta są połączone najkrótszymi możliwymi łukami (czyli geodezyjnymi); wśród krzywych na sferze są to odpowiedniki odcinków na płaszczyźnie. Kąt między dwoma bokami takiego trójkąta możemy definiować jako kąt między płaszczyznami wycinającymi je lub, równoważnie, jako kąt między odpowiednimi prostymi stycznymi.
Przykładowy trójkąt z rysunku 1 powstał w wyniku trzech wzajemnie prostopadłych cięć, a więc każdy z jego trzech kątów ma miarę  W rezultacie ich suma przekracza o
W rezultacie ich suma przekracza o 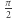 wartość, do której przyzwyczailiśmy się na płaszczyźnie!
wartość, do której przyzwyczailiśmy się na płaszczyźnie!
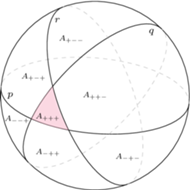
Rys. 2. Podział sfery na 8 obszarów
Gdyby coś nas podkusiło, żeby policzyć pole takiego trójkąta, to zauważylibyśmy, że osiem takich trójkątów składa się na całą sferę. Przyjąwszy promień sfery równy 1, otrzymujemy pole trójkąta: 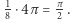 Czy zbieżność pola trójkąta z nadmiarem sumy kątów jest przypadkiem? Przekonamy się, że nie, dowodząc, że wzór na sumę kątów w trójkącie geodezyjnym na sferze o promieniu
Czy zbieżność pola trójkąta z nadmiarem sumy kątów jest przypadkiem? Przekonamy się, że nie, dowodząc, że wzór na sumę kątów w trójkącie geodezyjnym na sferze o promieniu  ma postać
ma postać
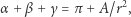 |
(*) |
gdzie 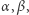
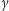 są kątami trójkąta, a
są kątami trójkąta, a 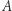 jego polem; jest to szczególny przypadek tak zwanego wzoru Gaussa-Bonneta.
jego polem; jest to szczególny przypadek tak zwanego wzoru Gaussa-Bonneta.
W tym celu oznaczmy płaszczyzny wycinające trójkąt jako  zgodnie z rysunkiem 2. Każda z tych płaszczyzn rozcina przestrzeń (i sferę) na dwie części - za dodatnią uznamy tę, w której leży nasz trójkąt, a tę drugą za ujemną. Możemy teraz wygodnie oznaczyć wszystkie wycięte obszary - np.
zgodnie z rysunkiem 2. Każda z tych płaszczyzn rozcina przestrzeń (i sferę) na dwie części - za dodatnią uznamy tę, w której leży nasz trójkąt, a tę drugą za ujemną. Możemy teraz wygodnie oznaczyć wszystkie wycięte obszary - np. 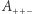 będzie obszarem leżącym po dodatniej stronie
będzie obszarem leżącym po dodatniej stronie 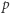 i
i 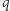 oraz po ujemnej stronie
oraz po ujemnej stronie 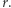 Zauważmy trzy zależności:
Zauważmy trzy zależności:
- Ze względu na symetrię środkową mamy
 oraz wszystkie inne tożsamości powstałe przez zamianę znaków na przeciwne.
oraz wszystkie inne tożsamości powstałe przez zamianę znaków na przeciwne. - Suma
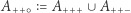 daje razem obszar leżący po dodatniej stronie płaszczyzn
daje razem obszar leżący po dodatniej stronie płaszczyzn 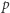 i
i 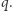 Pole takiego wycinka jest proporcjonalne do kąta między tymi płaszczyznami, a więc wynosi
Pole takiego wycinka jest proporcjonalne do kąta między tymi płaszczyznami, a więc wynosi  ; podobnie jest dla pozostałych obszarów tego typu.
; podobnie jest dla pozostałych obszarów tego typu. - Suma
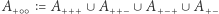 daje półsferę po dodatniej stronie
daje półsferę po dodatniej stronie 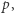 a zatem
a zatem 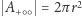 ; tak samo dla pozostałych półsfer.
; tak samo dla pozostałych półsfer.
Pozostaje nam zebrać te obserwacje, przeprowadzając rachunek oparty na wzorze włączeń i wyłączeń:

Z drugiej strony, obszar 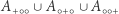 pokrywa całą sferę z wyjątkiem
pokrywa całą sferę z wyjątkiem 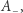 ma więc pole
ma więc pole
 |
Połączenie tych równości daje nam żądany wzór na pole trójkąta:
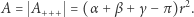 |

Rys. 3. Siatka odpowiadająca dwudziestościanowi foremnemu. Tutaj 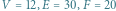
Pokażemy teraz, jak wykorzystać uzyskany związek do otrzymania wzoru Eulera.
Twierdzenie (Euler). Rozważmy na sferze dowolną siatkę złożoną z trójkątów geodezyjnych i oznaczmy przez  odpowiednio liczbę wierzchołków, krawędzi i trójkątów w tej siatce. Zachodzi wówczas równość
odpowiednio liczbę wierzchołków, krawędzi i trójkątów w tej siatce. Zachodzi wówczas równość
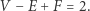 |
Dowód. Powtórzymy tutaj (choć w całkiem innym wydaniu) rozumowanie z artykułu Czy Ziemia jest płaska? A może jednak? (Delta 10/2016), zbadamy mianowicie sumę wszystkich kątów przy wierzchołkach. Ponieważ przy każdym wierzchołku kąty dodają się do 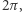 suma ta wynosi
suma ta wynosi 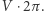 Z drugiej strony, sumę tę możemy otrzymać, dodając stronami zależności (*) dla wszystkich trójkątów w siatce - ponieważ pola trójkątów sumują się do całkowitego pola sfery, daje to
Z drugiej strony, sumę tę możemy otrzymać, dodając stronami zależności (*) dla wszystkich trójkątów w siatce - ponieważ pola trójkątów sumują się do całkowitego pola sfery, daje to  (bez straty ogólności przyjęliśmy
(bez straty ogólności przyjęliśmy 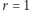 ). Po przyrównaniu tych dwóch wyników mamy
). Po przyrównaniu tych dwóch wyników mamy 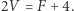 Pozostaje przypomnieć sobie, że każda ściana ma trzy krawędzie, a każda krawędź rozdziela dwie ściany, skąd wnioskujemy dodatkową zależność
Pozostaje przypomnieć sobie, że każda ściana ma trzy krawędzie, a każda krawędź rozdziela dwie ściany, skąd wnioskujemy dodatkową zależność  Te dwie równości pozwalają obliczyć
Te dwie równości pozwalają obliczyć
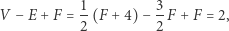 |
co kończy dowód.
Choć jest to istotnie trudniejsze do pokazania, analogiczną własność ma każda powierzchnia, nie tylko sfera. Wówczas wielkość 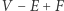 (zwana charakterystyką Eulera) zależy tylko i wyłącznie od powierzchni, a nie od wyboru siatki. Przykład powierzchni o charakterystyce Eulera równej 0 można znaleźć we wspomnianym już artykule.
(zwana charakterystyką Eulera) zależy tylko i wyłącznie od powierzchni, a nie od wyboru siatki. Przykład powierzchni o charakterystyce Eulera równej 0 można znaleźć we wspomnianym już artykule.
Wracając do zależności (*), Czytelnika może zdziwić, że znajomość kątów trójkąta pozwala na wyznaczenie pola - na płaszczyźnie przecież sprawa ma się zupełnie inaczej. Ten fenomen ma związek z niezerową krzywizną Gaussa sfery. Możemy nawet sformułować następującą definicję: jeśli na danej powierzchni dowolny trójkąt geodezyjny o kątach  i polu
i polu 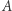 spełnia równość
spełnia równość
 |
to powiemy, że powierzchnia ta ma krzywiznę Gaussa stale równą 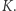 Dla takiej powierzchni pole trójkąta można wyznaczyć ze wzoru
Dla takiej powierzchni pole trójkąta można wyznaczyć ze wzoru  chyba że... wzór ten wymaga dzielenia przez zero! Ma to miejsce jedynie w przypadku płaszczyzny (lub jej "zwinięć", na przykład walca), dla której mamy
chyba że... wzór ten wymaga dzielenia przez zero! Ma to miejsce jedynie w przypadku płaszczyzny (lub jej "zwinięć", na przykład walca), dla której mamy 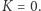 Nasz dowód pokazuje natomiast, że sfera o promieniu
Nasz dowód pokazuje natomiast, że sfera o promieniu  ma krzywiznę Gaussa równą
ma krzywiznę Gaussa równą 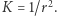 Odpowiada to dobrze intuicji mówiącej, że duże sfery są prawie płaskie - taka wydaje się na przykład powierzchnia Ziemi.
Odpowiada to dobrze intuicji mówiącej, że duże sfery są prawie płaskie - taka wydaje się na przykład powierzchnia Ziemi.
Idąc dalej za tą samą intuicją, moglibyśmy twierdzić, że powierzchnie o dużej krzywiźnie mają małe pole. Tak jest w istocie i podejmiemy ten temat w kontynuacji niniejszego artykułu, która ukaże się już za miesiąc. Jako pierwszy krok w tym kierunku proponuję poniższe zadanie.
Zadanie. Dana jest powierzchnia  wraz z siatką trójkątów, z których każdy w miejsce (*) spełnia nierówność
wraz z siatką trójkątów, z których każdy w miejsce (*) spełnia nierówność 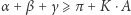 z tym samym parametrem
z tym samym parametrem  Wykażemy
Wykażemy
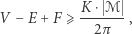 |
gdzie  jest polem
jest polem 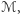 a
a 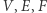 tak jak poprzednio oznaczają liczbę wierzchołków, krawędzi i trójkątów w siatce.
tak jak poprzednio oznaczają liczbę wierzchołków, krawędzi i trójkątów w siatce.
Uzasadnienie jest nietrudną modyfikacją dowodu twierdzenia Eulera, przy czym tutaj należy oczywiście operować na nierównościach. "Do przeczytania" za miesiąc!