Co to jest?
Geometria rzutowa
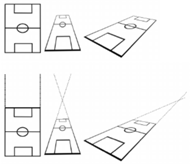
Geometria rzutowa to dział matematyki zajmujący się opisem tego, co nie zmienia się w figurach geometrycznych, gdy patrzymy na nie z różnych punktów widzenia. Innymi słowy: zróbmy zdjęcia figury z różnych stron i badajmy tylko to, co jest wspólne dla wszystkich zdjęć. Spoglądając z różnych stron na przykład na boisko piłkarskie, możemy stwierdzić, że raz wydaje nam się bliżej nieokreślonym czworokątem, raz trapezem, a z lotu ptaka - prostokątem.
koro odległości ani równoległość prostych nie zostają zachowane dla różnych zdjęć, to, jak łatwo się domyślić, w geometrii rzutowej nie ma miejsca dla twierdzenia Talesa ani Pitagorasa. Z drugiej strony, widzimy, że proste pozostają prostymi, a punkty punktami. A zatem właśnie o prostych, punktach i ich położeniu mówi geometria rzutowa.
Wydawać by się mogło, że płaszczyzna rzutowa nie powinna istotnie różnić się od euklidesowej. Aby się przekonać, czy tak jest w istocie, powróćmy na boisko piłkarskie. Spójrzmy na zdjęcie, na którym wygląda ono jak trapez. Z łatwością spostrzeżemy, że przedłużenia linii bocznych boiska przecinają się w jednym punkcie. Spójrzmy teraz na zdjęcie z lotu ptaka. Tutaj przedłużenia linii bocznych... wcale się nie przecinają. Nie można jednak sensownie mówić o położeniu prostych, jeśli nie da się stwierdzić, czy się przecinają, czy nie. Jedyne rozsądne rozwiązanie to dodanie do płaszczyzny tzw. punktów horyzontu. Jest to zupełnie naturalne właśnie dla naszej geometrii widzenia: przecież idąc torami kolejowymi, widzimy, że szyny łączą się w jednym punkcie na horyzoncie. Teraz już możemy spokojnie powiedzieć, że także na zdjęciu z lotu ptaka linie boczne boiska przecinają się. No tak, ale powinny przecież przecinać się w jednym punkcie, tak samo jak na zdjęciu z trapezem. Znów jedyne rozsądne rozwiązanie to utożsamienie dwóch przeciwległych punktów horyzontu, które od tej pory traktować będziemy jako jeden punkt. W ten sposób zakończyliśmy konstrukcję płaszczyzny rzutowej. (Należy jeszcze uzupełnić, że punkty horyzontu leżą na jednej prostej, którą trzeba dodać).
Przytoczony opis pochodzi z książki "Femme fatale. Trzy opowieści o królowej nauk" Witolda Sadowskiego. Szersze omówienie można znaleźć w książce "Co to jest matematyka?" Richarda Couranta i Herberta Robbinsa.
Czyli płaszczyznę rzutową można traktować jak zwykłą płaszczyznę, do której dołączono punkty w nieskończoności. Nieco formalniej: rozważmy płaszczyznę 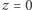 (czyli wszystkie punkty postaci
(czyli wszystkie punkty postaci 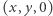 ) i oznaczmy ją przez
) i oznaczmy ją przez 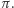 Punkt
Punkt 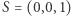 leży nad tą płaszczyzną.
leży nad tą płaszczyzną.
Każdy punkt płaszczyzny 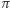 utożsamimy z prostą przechodzącą przez ten punkt i punkt
utożsamimy z prostą przechodzącą przez ten punkt i punkt 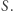 Jasne jest, że nie wykorzystaliśmy wszystkich prostych przechodzących przez
Jasne jest, że nie wykorzystaliśmy wszystkich prostych przechodzących przez 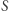 - a mianowicie prostych równoległych do płaszczyzny
- a mianowicie prostych równoległych do płaszczyzny 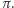 Zauważmy jeszcze, że punktom prostej
Zauważmy jeszcze, że punktom prostej 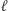 leżącej na
leżącej na 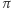 odpowiadają te proste przechodzące przez punkt
odpowiadają te proste przechodzące przez punkt 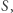 które leżą na płaszczyźnie wyznaczonej przez punkt
które leżą na płaszczyźnie wyznaczonej przez punkt 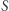 i prostą
i prostą 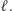 Niewykorzystana prosta to prosta przechodząca przez
Niewykorzystana prosta to prosta przechodząca przez 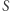 i równoległa do
i równoległa do 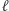 - nazwiemy ją punktem w nieskończoności prostej
- nazwiemy ją punktem w nieskończoności prostej 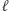 i oznaczymy przez
i oznaczymy przez 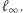 W takim razie prostym równoległym
W takim razie prostym równoległym 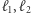 leżącym na
leżącym na 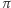 odpowiada ta sama prosta
odpowiada ta sama prosta 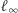 przechodząca przez
przechodząca przez 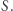 Proste równoległe (stały się płaszczyznami) przecinają się teraz w nieskończoności wzdłuż prostej
Proste równoległe (stały się płaszczyznami) przecinają się teraz w nieskończoności wzdłuż prostej 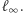 Płaszczyzna rzutowa może być potraktowana jako zbiór wszystkich prostych przechodzących przez
Płaszczyzna rzutowa może być potraktowana jako zbiór wszystkich prostych przechodzących przez 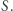 Rozsądnie jest określić odległość punktów, czyli prostych przechodzących przez
Rozsądnie jest określić odległość punktów, czyli prostych przechodzących przez 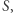 jako kąt między tymi prostymi.
jako kąt między tymi prostymi.
Można płaszczyznę rzutową opisać inaczej: rozpatrzmy przekształcenie 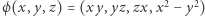 (z przestrzeni
(z przestrzeni 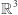 w
w 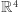 ), które ograniczymy jedynie do punktów sfery o promieniu
), które ograniczymy jedynie do punktów sfery o promieniu 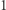 i środku
i środku 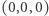 - więc punktów, dla których
- więc punktów, dla których 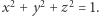 Każda prosta przechodząca przez punkt
Każda prosta przechodząca przez punkt 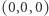 przebija opisaną sferę w dwóch punktach. Jeśli jednym z nich jest
przebija opisaną sferę w dwóch punktach. Jeśli jednym z nich jest 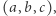 to drugim jest
to drugim jest 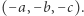 Można się przekonać, że
Można się przekonać, że 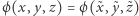 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 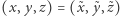 albo
albo 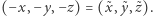 Można więc utożsamić prostą przechodzącą przez punkty
Można więc utożsamić prostą przechodzącą przez punkty 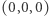 oraz
oraz 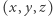 z punktem
z punktem 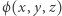 (leżącym w czterowymiarowej przestrzeni). Niech zbiór
(leżącym w czterowymiarowej przestrzeni). Niech zbiór 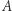 składa się z tych punktów sfery, których współrzędne spełniają warunki:
składa się z tych punktów sfery, których współrzędne spełniają warunki: 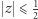 i
i 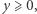 a
a 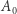 z tych punktów zbioru
z tych punktów zbioru 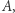 dla których
dla których 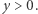 Na zbiorze
Na zbiorze 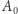 przekształcenie
przekształcenie 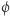 jest różnowartościowe. Natomiast
jest różnowartościowe. Natomiast 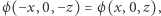 więc przekształcenie
więc przekształcenie 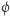 przekształca punkty
przekształca punkty 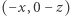 i
i 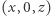 na ten sam punkt (skleja je). Przekształcenie
na ten sam punkt (skleja je). Przekształcenie 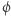 skleja "końcowe" punkty pasa
skleja "końcowe" punkty pasa 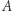 z "przekręceniem". Powstały twór to wstęga Möbiusa. Jej brzeg to jedna linia (dzięki "przekręceniu"). Przekształcenie
z "przekręceniem". Powstały twór to wstęga Möbiusa. Jej brzeg to jedna linia (dzięki "przekręceniu"). Przekształcenie 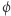 odwzorowuje zbiór
odwzorowuje zbiór 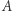 oraz zbiór złożony ze wszystkich punktów sfery, dla których
oraz zbiór złożony ze wszystkich punktów sfery, dla których 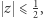 na ten sam zbiór. Zbiór tych punktów sfery, dla których
na ten sam zbiór. Zbiór tych punktów sfery, dla których 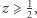 można w naturalny sposób utożsamić z kołem. Możemy więc powiedzieć, że płaszczyzna rzutowa powstaje przez sklejenie brzegami koła ze wstęgą Möbiusa.
można w naturalny sposób utożsamić z kołem. Możemy więc powiedzieć, że płaszczyzna rzutowa powstaje przez sklejenie brzegami koła ze wstęgą Möbiusa.
W artykułach Dobble, Delta 06/2018 oraz Naprawdę ciekawa gra, Delta 04/2014 można przeczytać o przyjemnym zastosowaniu płaszczyzny rzutowej, a jeszcze więcej w Czy widział ktoś płaszczyznę rzutową?, Delta 06/2011.