Geometria Bolyaia–Łobaczewskiego

Najdłużej badanym problemem matematycznym była kwadratura koła. Zaraz za nią uplasowała się kwestia piątego postulatu Euklidesa. Chodziło o to, czy zdanie "jeśli dwie proste przecięte trzecią tworzą kąty wewnętrzne jednostronne o sumie mniejszej od dwóch kątów prostych, to proste te po przedłużeniu przetną się i to właśnie z tej strony" spełnia wymagane dla postulatów warunki, czyli czy wyraża rzeczy jasne i oczywiste i czy jest dostatecznie zwięzłe, by być uznane za pierwotną prawdę. Debatę zapoczątkował w V wieku Proklos, odpowiadając dwukrotnie nie i proponując, by wykazać, że usunięcie tego postulatu gmachu geometrii nie naruszy.
Z biegiem stuleci angażowali się w te rozważania również przedstawiciele innych gałęzi nauki, aż do orzeczenia, że debata jest nonsensowna, bo z geometrią niejako się rodzimy (Kant, Krytyka czystego rozumu). I wtedy (początek XIX wieku) dwóch młodych ludzi, Węgier Janos Bolyai i Rosjanin Nikołaj Łobaczewski, uparło się, by świat przyjął, że usunięcie piątego postulatu nie tyle narusza gmach geometrii, co go dość gruntownie przebudowuje. Spotkała ich za to surowa kara, ale odnieśli zwycięstwo, bo od tej pory wszyscy matematycy uznali istnienie alternatywnych geometrii, choć było to dla nich (i w ogóle dla całego świata nauki) równie wstrząsające, jak dla nas byłby kontakt z inną cywilizacją.


Powstał też problem, jak taka alternatywna geometria wygląda, bo umiano pokazać jej poszczególne fenomena, ale w całości jej "zobaczyć" nie umiano. Zanim (za sprawą Kleina) takie całościowe spojrzenie zostało skonstruowane, okazało się, że alternatywnych geometrii jest wiele. Wystarczyło bowiem, by (poniekąd przymusowo) sprawę zreferował na swoim wykładzie habilitacyjnym działający w analizie matematycznej Bernard Riemann. Wskazał on, jak można opisać nieskończoną mnogość struktur matematycznych, które od naszej geometrii będą różne, będąc jednak geometriami. Skorzystamy dalej z jego pomysłu.
Po co matematyce modele?
Jeśli w jakiejś teorii A, o której jesteśmy przekonani, że jest niesprzeczna, zbudujemy model teorii B (czyli strukturę, mającą taką budowę jak teoria B), to z równym przekonaniem możemy stwierdzić, że teoria B też jest niesprzeczna. Dlatego tworząc nowe teorie, konstruuje się ich modele w klasycznej geometrii lub arytmetyce.
Ale jest i inny powód. Posiadanie różnych modeli interesującej nas teorii pozwala "trochę oszczędzić" na dowodzeniu. Jeśli bowiem dostrzegamy jakąś prawidłowość w modelu, to (jeśli nie ma tam specyficznych własności materii, z której model został zbudowany) możemy zaobserwowaną prawidłowość uznać za własność modelowanej teorii.
Tak w większości przypadków będziemy postępowali tutaj, właśnie przez oglądanie takich modeli, w których te czy inne własności będą wręcz rzucały się w oczy. Rodzinę modeli geometrii Bolyaia-Łobaczewskiego, którymi będziemy się posługiwali, skonstruujemy, wychodząc od modelu zbudowanego przez Henri Poincarégo w myśl wskazań Riemanna.
Koncepcja Riemanna jest następująca. Określamy obiekt, który będzie w naszym modelu pełnił funkcję zbioru punktów i dla tych (nowo mianowanych) punktów określamy iloczyn skalarny. Gdy punkty są parami liczb rzeczywistych, ów iloczyn skalarny punktów 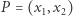 i
i 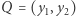 to liczba
to liczba

gdzie 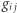 są dobrane w ten sposób, by liczba
są dobrane w ten sposób, by liczba 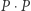 była zawsze nieujemna.
była zawsze nieujemna.
Dysponując iloczynem skalarnym, określamy długość wektora  jako
jako 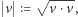 a kąty mierzymy, obliczając ich kosinus według wzoru
a kąty mierzymy, obliczając ich kosinus według wzoru 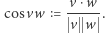
Na przykład geometria zwykłej płaszczyzny to zbiór 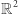 z iloczynem danym przez
z iloczynem danym przez 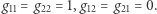
Model Poincarégo na półpłaszczyźnie (mPpp)
Gdy zbiorem punktów będzie 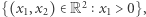 a iloczyn skalarny dany będzie przez
a iloczyn skalarny dany będzie przez 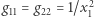 i
i 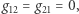 to będziemy mieli do czynienia z modelem płaszczyzny Bolyaia-Łobaczewskiego. Rzut oka na wzór na kosinus od razu pozwala zauważyć, że model ten jest euklidesowokątny, co oznacza, że narysowane krzywe w naszym modelu w sensie płaszczyzny Bolyaia-Łobaczewskiego tworzą kąt o tej samej rozwartości, jak ten, który widzimy euklidesowym okiem na rysunku (owe
to będziemy mieli do czynienia z modelem płaszczyzny Bolyaia-Łobaczewskiego. Rzut oka na wzór na kosinus od razu pozwala zauważyć, że model ten jest euklidesowokątny, co oznacza, że narysowane krzywe w naszym modelu w sensie płaszczyzny Bolyaia-Łobaczewskiego tworzą kąt o tej samej rozwartości, jak ten, który widzimy euklidesowym okiem na rysunku (owe 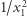 w liczniku i mianowniku się skrócą). Zatem inne pojęcia geometrii Bolyai-Łobaczewskiego (np. proste) muszą w naszym modelu wyglądać inaczej niż ich euklidesowe odpowiedniki - gdyby bowiem wyglądały tak samo, otrzymalibyśmy nie geometrię Bolyaia-Łobaczewskiego, lecz geometrię półpłaszczyzny euklidesowej.
w liczniku i mianowniku się skrócą). Zatem inne pojęcia geometrii Bolyai-Łobaczewskiego (np. proste) muszą w naszym modelu wyglądać inaczej niż ich euklidesowe odpowiedniki - gdyby bowiem wyglądały tak samo, otrzymalibyśmy nie geometrię Bolyaia-Łobaczewskiego, lecz geometrię półpłaszczyzny euklidesowej.
Nie wchodząc w szczegóły różniczkowej obróbki tego modelu, przyjmijmy, że udało się nam stwierdzić, iż prostą opisanę za pomocą tego iloczynu skalarnego (jedną, konkretną prostą) w tym modelu jest 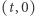 dla
dla  a jej punkty są sparametryzowane za pomocą długości
a jej punkty są sparametryzowane za pomocą długości  jako
jako 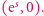 Zatem odległość punktów
Zatem odległość punktów 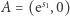 i
i 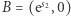 jest w geometrii Bolyai-Łobaczewskiego równa
jest w geometrii Bolyai-Łobaczewskiego równa

gdzie symbol, który znajduje się między wartościami bezwzględnymi wewnątrz logarytmu w ostatnim członie powyższej równości, to dwustosunek (patrz str. 14), a symbolem  został oznaczony kierunek prostej. Ten kierunek, podobnie jak punkt
został oznaczony kierunek prostej. Ten kierunek, podobnie jak punkt 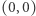 nie należy do modelu, nie jest punktem modelowanej płaszczyzny B-Ł, ale - można powiedzieć, że oba te punkty "kończą" prostą. Dlatego też Hilbert wprowadził zwyczaj nazywania ich końcami prostej. W mPpp odległość punktów będziemy mierzyli za pomocą dwustosunku:
nie należy do modelu, nie jest punktem modelowanej płaszczyzny B-Ł, ale - można powiedzieć, że oba te punkty "kończą" prostą. Dlatego też Hilbert wprowadził zwyczaj nazywania ich końcami prostej. W mPpp odległość punktów będziemy mierzyli za pomocą dwustosunku:

Te skąpe wiadomości wzięte na wiarę pozwolą nam poznać wiele własności geometrii Bolyaia-Łobaczewskiego za pomocą mPpp i innych modeli.
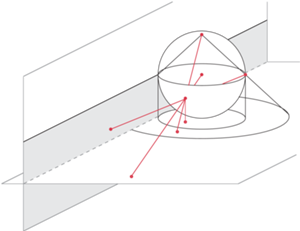
Innych, bo z mPpp można w prosty sposób uzyskać jeszcze inne przydatne modele. Widoczna na rysunku obok półsfera jest styczna do brzegu rozpatrywanej dotąd (szarej) półpłaszczyzny. Można na nią zrzutować stereograficznie mPpp, otrzymując model Poincarégo na półsferze (mPp). On z kolei może być zrzutowany stereograficznie (z najwyższego punktu "drugiej połowy" półsfery) na płaszczyznę styczną do półsfery w jej "południowym" biegunie - tak otrzymamy model Poincarégo w kole (mPk). Możemy też mPp zrzutować prostokątnie na tę samą płaszczyznę - powstanie model Kleina (mK), też w kole, ale mniejszym (zamiast na dół można rzutować do góry na koło "zamykające" półsferę). Jeszcze inny model otrzymamy, rzutując mPp na tę płaszczyznę ze środka półsfery - ten model (mp) działać będzie na całej płaszczyźnie.
Zawarcie bliższej znajomości z tymi modelami pozwala na obserwowanie rozmaitych faktów mających miejsce w geometrii B-Ł. Część z nich postaram się zaprezentować.
- Cały artykuł dostępny jest w wersji do druku [application/pdf]: (557 KB)
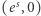 ma w modelu współrzędne
ma w modelu współrzędne