O trójkątach (nie tylko) na sferze
Rozpocznijmy od przypomnienia, czym jest trójkąt geodezyjny. Mając dane dwa punkty na powierzchni (powiedzmy, że leżące odpowiednio blisko siebie), najkrótszą łączącą je krzywą leżącą na tej powierzchni nazwiemy geodezyjną. Dla przykładu - na płaszczyźnie tę rolę pełnią odcinki, a na sferze łuki tzw. okręgów wielkich. Przez trójkąt geodezyjny rozumiemy obszar wyznaczony przez trzy punkty, zamknięty między łączącymi je geodezyjnymi. Kąt w wierzchołku takiego trójkąta liczymy jako kąt między stycznymi do odpowiednich krzywych geodezyjnych.
W poprzednim numerze (Delcie 2/2019), w artykule O trójkątach na sferze, wprowadziliśmy pojęcie krzywizny Gaussa, opierając się na przykładzie sfer o różnych promieniach. Przypomnijmy je w trochę zmienionej wersji: jeśli na danej powierzchni 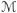 dowolny trójkąt geodezyjny o kątach
dowolny trójkąt geodezyjny o kątach 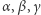 i polu
i polu 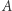 spełnia nierówność
spełnia nierówność
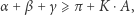 |
(*) |
to powiemy, że powierzchnia ta ma krzywiznę Gaussa ograniczoną z dołu przez 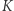 . Jeśli (*) jest zawsze równością, to mówimy, że krzywizna Gaussa jest równa
. Jeśli (*) jest zawsze równością, to mówimy, że krzywizna Gaussa jest równa 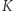 . W świetle tej definicji płaszczyzna ma zerową krzywiznę Gaussa, natomiast okazuje się, że sfera o promieniu
. W świetle tej definicji płaszczyzna ma zerową krzywiznę Gaussa, natomiast okazuje się, że sfera o promieniu  ma krzywiznę równą
ma krzywiznę równą 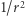 , co wykazaliśmy w poprzednim artykule.
, co wykazaliśmy w poprzednim artykule.
Celem tego artykułu jest uzasadnienie następującej zależności pola całej powierzchni 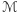 od jej krzywizny:
od jej krzywizny:
Twierdzenie. Jeśli 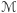 jest spójną powierzchnią o krzywiźnie Gaussa ograniczonej z dołu przez
jest spójną powierzchnią o krzywiźnie Gaussa ograniczonej z dołu przez  , to jej pole
, to jej pole 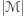 spełnia nierówność
spełnia nierówność
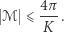 |
Warto odnotować, że dla dowolnej sfery ta nierówność staje się równością.
Na potrzeby dowodu zacznijmy od nałożenia na 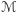 siatki złożonej z trójkątów geodezyjnych, oznaczmy przez
siatki złożonej z trójkątów geodezyjnych, oznaczmy przez  ,
, 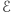 ,
, 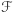 odpowiednio zbiory wierzchołków, krawędzi i trójkątów w tej siatce, a przez
odpowiednio zbiory wierzchołków, krawędzi i trójkątów w tej siatce, a przez 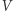 ,
, 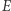 ,
, 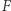 liczności tych zbiorów. Zadanie pozostawione na koniec poprzedniego artykułu pokazuje, że
liczności tych zbiorów. Zadanie pozostawione na koniec poprzedniego artykułu pokazuje, że
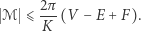 |
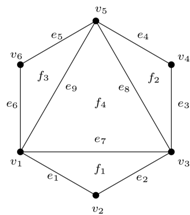
Na powyższym rysunku:
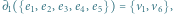

Pozostaje więc wykazać nierówność 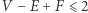 . Sprowadziliśmy więc dowód twierdzenia do następującego faktu:
. Sprowadziliśmy więc dowód twierdzenia do następującego faktu:
Lemat. Jeśli spójna powierzchnia 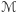 jest pokryta trójkątną siatką, to
jest pokryta trójkątną siatką, to  nie przekracza 2.
nie przekracza 2.
Aby ten fakt uzasadnić, wprowadzimy narzędzie pomocnicze, w którym odpowiednio doświadczony życiem Czytelnik może rozpoznać homologie symplicjalne o współczynnikach w 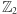 .
.
Wprowadźmy zbiory potęgowe (czyli zbiory wszystkich podzbiorów) 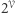 ,
, 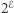 ,
, 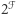 i określmy tak zwany operator brzegu
i określmy tak zwany operator brzegu 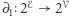 :
:
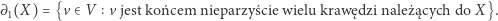 |
Analogicznie definiujemy drugi operator brzegu  :
:
 |
Nazwa operator brzegu bierze się stąd, że 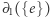 to dwuelementowy zbiór końców krawędzi
to dwuelementowy zbiór końców krawędzi  , a
, a 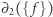 jest zbiorem trzech boków ściany
jest zbiorem trzech boków ściany 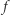 .
.

Różnica symetryczna trójkąta i kwadratu zaznaczona jest kolorem.
Dla dowodu kluczowa jest pewna własność tych operatorów, którą nazwiemy tutaj liniowością. Mianowicie operator 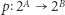 nazwiemy liniowym, jeśli
nazwiemy liniowym, jeśli
 |
gdzie 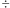 oznacza różnicę symetryczną dwóch zbiorów. Sprawdzenie liniowości operatorów
oznacza różnicę symetryczną dwóch zbiorów. Sprawdzenie liniowości operatorów 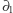 i
i 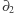 zostawimy Czytelnikowi jako ćwiczenie (rozwiązanie tutaj).
zostawimy Czytelnikowi jako ćwiczenie (rozwiązanie tutaj).
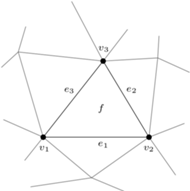
Równość 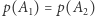 jest równoważna równości
jest równoważna równości  , co (jeśli
, co (jeśli 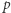 jest liniowy) zachodzi dokładnie wtedy, gdy
jest liniowy) zachodzi dokładnie wtedy, gdy 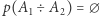 . Stąd wynika, że
. Stąd wynika, że 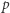 przyjmuje każdą swoją wartość tyle samo razy, a mianowicie
przyjmuje każdą swoją wartość tyle samo razy, a mianowicie 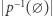 razy. Oznacza to, że zbiór
razy. Oznacza to, że zbiór  można podzielić na
można podzielić na 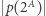 podzbiorów, każdy o liczności
podzbiorów, każdy o liczności 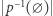 , co daje nam równość
, co daje nam równość
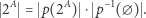 |
(1) |
Ustalmy ścianę 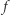 i oznaczmy jej krawędzie oraz wierzchołki jak na rysunku, wówczas
i oznaczmy jej krawędzie oraz wierzchołki jak na rysunku, wówczas 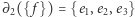 . Widzimy teraz, że każdy z wierzchołków
. Widzimy teraz, że każdy z wierzchołków  należy do dwóch krawędzi z otrzymanego zbioru, natomiast każdy pozostały wierzchołek nie należy do żadnego. Jako że 0 i 2 są liczbami parzystymi, wnioskujemy, że
należy do dwóch krawędzi z otrzymanego zbioru, natomiast każdy pozostały wierzchołek nie należy do żadnego. Jako że 0 i 2 są liczbami parzystymi, wnioskujemy, że 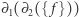 jest zbiorem pustym. Korzystając z liniowości operatorów
jest zbiorem pustym. Korzystając z liniowości operatorów 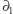 i
i 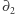 (i indukcji względem
(i indukcji względem 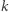 ), możemy wyprowadzić równość
), możemy wyprowadzić równość 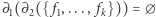 dla dowolnego podzbioru
dla dowolnego podzbioru  rodziny
rodziny 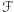 . Oznacza to, że jeśli
. Oznacza to, że jeśli 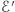 jest wartością
jest wartością 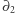 (czyli jest elementem
(czyli jest elementem 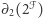 ), to
), to 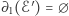 (czyli
(czyli 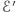 jest elementem
jest elementem 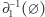 ). Zbiór
). Zbiór 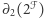 jest więc podzbiorem
jest więc podzbiorem 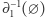 , w związku z czym
, w związku z czym
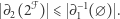 |
(2) |
Wprost z definicji 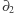 wynika, że
wynika, że 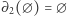 oraz
oraz 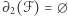 ; sprawdzimy teraz, że istotnie
; sprawdzimy teraz, że istotnie  . Rozważmy mianowicie podzbiór
. Rozważmy mianowicie podzbiór 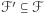 , dla którego
, dla którego 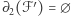 . Warunek ten oznacza, że jeśli jakaś ściana należy do
. Warunek ten oznacza, że jeśli jakaś ściana należy do  , to każda ze ścian sąsiadujących również należy do
, to każda ze ścian sąsiadujących również należy do 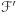 . Ponieważ
. Ponieważ 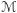 jest powierzchnią spójną, łatwo zauważyć, że wówczas wszystkie ściany muszą należeć do
jest powierzchnią spójną, łatwo zauważyć, że wówczas wszystkie ściany muszą należeć do 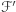 . Pozostawia to dwa możliwe przypadki:
. Pozostawia to dwa możliwe przypadki:  oraz
oraz 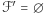 .
.
Wykażemy również, że 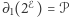 , gdzie
, gdzie 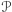 jest rodziną wszystkich parzystoelementowych podzbiorów
jest rodziną wszystkich parzystoelementowych podzbiorów 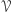 . Zauważmy najpierw, że
. Zauważmy najpierw, że 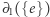 jest zbiorem dwuelementowym, a więc
jest zbiorem dwuelementowym, a więc 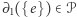 . Ponieważ różnica symetryczna dwóch zbiorów parzystej mocy również jest parzystej mocy, ogólny warunek
. Ponieważ różnica symetryczna dwóch zbiorów parzystej mocy również jest parzystej mocy, ogólny warunek 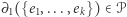 łatwo otrzymujemy z liniowości
łatwo otrzymujemy z liniowości 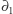 przez indukcję ze względu na
przez indukcję ze względu na 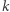 . Stąd zawieranie
. Stąd zawieranie 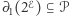 . Dla dowodu przeciwnego zawierania rozważmy najpierw dowolny dwuelementowy zbiór wierzchołków
. Dla dowodu przeciwnego zawierania rozważmy najpierw dowolny dwuelementowy zbiór wierzchołków 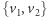 . Dzięki spójności
. Dzięki spójności 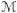 możemy znaleźć łamaną
możemy znaleźć łamaną 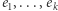 prowadzącą z
prowadzącą z 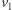 do
do 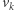 ; wprost z definicji mamy wtedy
; wprost z definicji mamy wtedy 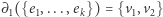 . Ogólny przypadek ponownie otrzymujemy przez indukcję. Jeśli dla dowolnych
. Ogólny przypadek ponownie otrzymujemy przez indukcję. Jeśli dla dowolnych 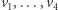 umiemy znaleźć podzbiory
umiemy znaleźć podzbiory 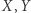 spełniające
spełniające 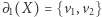 i
i  , to
, to
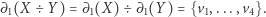 |
Iterując to rozumowanie, otrzymujemy odpowiedni zbiór krawędzi dla każdego parzystoelementowego zbioru wierzchołków.
Z powyższych dwóch akapitów wynika, że
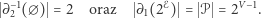 |
(3) |
Ostatnia równość wynika stąd, że jeśli ustalimy dowolny wierzchołek 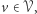 to
to
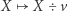 |
zadaje bijekcję między rodziną  a dopełnieniem tej rodziny.
a dopełnieniem tej rodziny.
Wykorzystując równości (1), (2) i (3), otrzymujemy
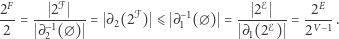 |
Po zlogarytmowaniu obu stron odczytujemy nierówność  , która kończy dowód lematu, przez to również uzasadnienie twierdzenia, w konsekwencji niestety niniejszy artykuł. A wszystko zaczęło się tak niewinnie, od sumy kątów w trójkącie...
, która kończy dowód lematu, przez to również uzasadnienie twierdzenia, w konsekwencji niestety niniejszy artykuł. A wszystko zaczęło się tak niewinnie, od sumy kątów w trójkącie...
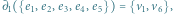
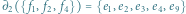
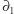 , ale uzasadnienie dla
, ale uzasadnienie dla 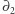 przebiega analogicznie. Ustalmy dwa podzbiory krawędzi
przebiega analogicznie. Ustalmy dwa podzbiory krawędzi 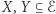 oraz wierzchołek
oraz wierzchołek 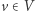 . Jeśli na chwilę ograniczymy się jedynie do krawędzi kończących się w
. Jeśli na chwilę ograniczymy się jedynie do krawędzi kończących się w 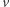 , to liczba krawędzi z
, to liczba krawędzi z  ma tę samą parzystość co suma liczby krawędzi z
ma tę samą parzystość co suma liczby krawędzi z 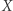 i liczby krawędzi z
i liczby krawędzi z 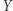 . Aby ta ostatnia suma była nieparzysta, dokładnie jeden ze składników musi być nieparzysty, a drugi parzysty. Innymi słowy,
. Aby ta ostatnia suma była nieparzysta, dokładnie jeden ze składników musi być nieparzysty, a drugi parzysty. Innymi słowy, 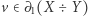 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 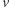 należy do dokładnie jednego ze zbiorów
należy do dokładnie jednego ze zbiorów 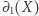 i
i 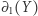 . W języku różnicy symetrycznej oznacza to dokładnie równość
. W języku różnicy symetrycznej oznacza to dokładnie równość 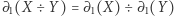 .
.