Newtonowskie intuicje dla fal grawitacyjnych
Według ogólnej teorii względności grawitacja jest skutkiem zakrzywiania się czterowymiarowej czasoprzestrzeni wokół masywnych obiektów. Mniej masywne ciała poruszają się wokół bardziej masywnych po liniach geodezyjnych (liniach "najprostszych" w zakrzywionej przestrzeni), co np. w przypadku planet w Układzie Słonecznym daje wrażenie ruchu po orbitach eliptycznych. Na swobodnie poruszające się ciała nie działa żadna siła: ich trajektorie są wynikiem geometrii.

Dodatkowo, ogólna teoria względności ma wbudowane ograniczenie prędkości. Wszelkie informacje o zmianie krzywizny rozprzestrzeniają się z prędkością światła. O zmianach tych można myśleć jak o zmiennej w czasie odległości czasoprzestrzennej pomiędzy zdarzeniami. Odległość ta, czyli czterowymiarowy interwał 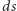 definiuje się, używając tensora metrycznego
definiuje się, używając tensora metrycznego 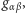
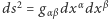 (zakres
(zakres 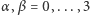 odpowiada jednemu wymiarowi czasowemu i trzem przestrzennym, a powtarzające się indeksy oznaczają sumowanie w tym zakresie). Składowe
odpowiada jednemu wymiarowi czasowemu i trzem przestrzennym, a powtarzające się indeksy oznaczają sumowanie w tym zakresie). Składowe 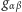 w ogólnym przypadku mogą mieć skomplikowaną postać zależną od rozmieszczenia zakrzywiających czasoprzestrzeń mas. Dla ilustracji rozważmy przypadek pustej czasoprzestrzeni (czasoprzestrzeni Minkowskiego, z dala od jakichkolwiek mas), z dodanym drobnym zaburzeniem. Interwał czasoprzestrzenny jest wtedy równy
w ogólnym przypadku mogą mieć skomplikowaną postać zależną od rozmieszczenia zakrzywiających czasoprzestrzeń mas. Dla ilustracji rozważmy przypadek pustej czasoprzestrzeni (czasoprzestrzeni Minkowskiego, z dala od jakichkolwiek mas), z dodanym drobnym zaburzeniem. Interwał czasoprzestrzenny jest wtedy równy

gdzie 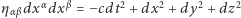 jest czterowymiarową "odległością" w pustej przestrzeni, a
jest czterowymiarową "odległością" w pustej przestrzeni, a 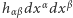 jej niewielkim zaburzeniem. Wkrótce po ogłoszeniu ogólnej teorii względności, w 1916 roku Albert Einstein stwierdził, że w przypadku przedstawionym powyżej jego równania przyjmują postać równania falowego, którego rozwiązaniem jest owo małe zaburzenie
jej niewielkim zaburzeniem. Wkrótce po ogłoszeniu ogólnej teorii względności, w 1916 roku Albert Einstein stwierdził, że w przypadku przedstawionym powyżej jego równania przyjmują postać równania falowego, którego rozwiązaniem jest owo małe zaburzenie 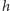 : fala grawitacyjna. Ma ono parę cech podobnych do fal elektromagnetycznych: ma charakter fali poprzecznej i ma (dwie) niezależne polaryzacje. Przez następne kilkadziesiąt lat istniała poważna kontrowersja, czy rozwiązaniom tym odpowiada zjawisko fizyczne, czy raczej są efektem doboru współrzędnych. Kontrowersja została rozwiana na przełomie lat 50. i 60. przez Feliksa Piraniego, Hermana Bondiego, Ivora Robinsona i Andrzeja Trautmana na korzyść prawdziwości hipotezy fal grawitacyjnych.
: fala grawitacyjna. Ma ono parę cech podobnych do fal elektromagnetycznych: ma charakter fali poprzecznej i ma (dwie) niezależne polaryzacje. Przez następne kilkadziesiąt lat istniała poważna kontrowersja, czy rozwiązaniom tym odpowiada zjawisko fizyczne, czy raczej są efektem doboru współrzędnych. Kontrowersja została rozwiana na przełomie lat 50. i 60. przez Feliksa Piraniego, Hermana Bondiego, Ivora Robinsona i Andrzeja Trautmana na korzyść prawdziwości hipotezy fal grawitacyjnych.
Realne promieniowanie jest związane z transportem energii; w szczególności fale powinny móc przenosić energię od źródła do nieskończoności. Jeśli amplituda pola związanego z (dla uproszczenia) sferyczną falą w odległości  od źródła jest równa
od źródła jest równa 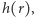 to strumień energii przez sferyczną powierzchnię wynosi
to strumień energii przez sferyczną powierzchnię wynosi 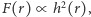 a całkowita moc promieniowania (jasność) jest proporcjonalna do
a całkowita moc promieniowania (jasność) jest proporcjonalna do 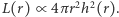 Jako że energia musi być zachowana, amplituda
Jako że energia musi być zachowana, amplituda 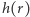 musi maleć z odległością jak
musi maleć z odległością jak 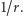 W przypadku detektorów fal grawitacyjnych typu laserowych interferometrów Advanced LIGO i Advanced Virgo, które mierzą właśnie amplitudę fali
W przypadku detektorów fal grawitacyjnych typu laserowych interferometrów Advanced LIGO i Advanced Virgo, które mierzą właśnie amplitudę fali 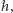 mierzona jest względna różnica różnic długości prostopadłych ramion interferometru,
mierzona jest względna różnica różnic długości prostopadłych ramion interferometru, 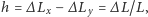 gdzie
gdzie 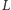 jest długością ramienia (więcej szczegółów w artykule Izy Kowalskiej w Delcie 10/2010). Zależność
jest długością ramienia (więcej szczegółów w artykule Izy Kowalskiej w Delcie 10/2010). Zależność 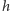 od odwrotności odległości przekłada się na daleko większy zasięg w porównaniu do tradycyjnych metod obserwacji, w których wartością mierzoną jest energia proporcjonalna do
od odwrotności odległości przekłada się na daleko większy zasięg w porównaniu do tradycyjnych metod obserwacji, w których wartością mierzoną jest energia proporcjonalna do 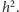 Poprawa czułości o rząd wielkości oznacza dziesięciokrotnie dalszy zasięg w porównaniu do około trzykrotnie większego zasięgu np. teleskopów optycznych.
Poprawa czułości o rząd wielkości oznacza dziesięciokrotnie dalszy zasięg w porównaniu do około trzykrotnie większego zasięgu np. teleskopów optycznych.
Przez analogię do elektromagnetyzmu, w którym promieniowanie elektromagnetyczne jest skutkiem przyśpieszonego ruchu ładunków elektrycznych, źródłem promieniowania grawitacyjnego powinien być przyśpieszony ruch mas. Do promieniowania nie wystarczy jednak samo istnienie ładunku (masy). Dla układu mas opisanego rozkładem gęstości 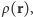 gdzie
gdzie 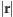 to radialna odległość od początku układu odniesienia (np. środka masy), najprostszym momentem rozkładu jest monopol
to radialna odległość od początku układu odniesienia (np. środka masy), najprostszym momentem rozkładu jest monopol 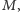 który jest po prostu całkowitą masą-energią układu. Jego zmiana oznaczałaby nieprzestrzeganie zasady zachowania masy-energii. Również zmienny moment dipolowy mas
który jest po prostu całkowitą masą-energią układu. Jego zmiana oznaczałaby nieprzestrzeganie zasady zachowania masy-energii. Również zmienny moment dipolowy mas 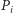 nie może być źródłem promieniowania grawitacyjnego, ponieważ z definicji odpowiada środkowi masy układu; zmienność oznaczałaby złamanie zasady zachowania pędu. Najniższym "promieniującym" multipolem w teorii grawitacji jest zatem kwadrupol,
nie może być źródłem promieniowania grawitacyjnego, ponieważ z definicji odpowiada środkowi masy układu; zmienność oznaczałaby złamanie zasady zachowania pędu. Najniższym "promieniującym" multipolem w teorii grawitacji jest zatem kwadrupol, 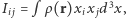 z którym nie wiążą się żadne zasady zachowania. Powyższe rozważania oznaczają, że sferycznie symetryczny ruch mas, np. kolaps albo eksplozja, nie wywołuje emisji fal grawitacyjnych. To samo dotyczy osiowo symetrycznej rotującej gwiazdy. Dobrymi źródłami fal są natomiast niesferyczne wybuchy supernowych, rotujące zdeformowane gwiazdy neutronowe oraz układy podwójne gwiazd lub czarnych dziur.
z którym nie wiążą się żadne zasady zachowania. Powyższe rozważania oznaczają, że sferycznie symetryczny ruch mas, np. kolaps albo eksplozja, nie wywołuje emisji fal grawitacyjnych. To samo dotyczy osiowo symetrycznej rotującej gwiazdy. Dobrymi źródłami fal są natomiast niesferyczne wybuchy supernowych, rotujące zdeformowane gwiazdy neutronowe oraz układy podwójne gwiazd lub czarnych dziur.
Wielkość amplitudy fali grawitacyjnej 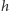 można oszacować za pomocą analizy wymiarowej. Z definicji
można oszacować za pomocą analizy wymiarowej. Z definicji 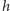 jest wielkością bezwymiarową i, jak wynika z powyższych rozważań, odwrotnie proporcjonalną do odległości od źródła. Powinna też być związana z momentem kwadrupolowym, którego jednostki to [kgm
jest wielkością bezwymiarową i, jak wynika z powyższych rozważań, odwrotnie proporcjonalną do odległości od źródła. Powinna też być związana z momentem kwadrupolowym, którego jednostki to [kgm 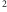 ]. Wiemy także, że w wyrażeniu powinna pojawić się druga pochodna, odpowiadająca przyśpieszonemu ruchowi mas, niech zatem
]. Wiemy także, że w wyrażeniu powinna pojawić się druga pochodna, odpowiadająca przyśpieszonemu ruchowi mas, niech zatem 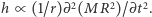 Jednostki tego wyrażenia to
Jednostki tego wyrażenia to ![−2 |[kgms ].](/math/temat/fizyka/grawitacja_i_wszechswiat/2017/02/26/Newtonowskie_intuicje_dla_fal_gr/5x-1bf4270b496344fba58c14f17d5cbebbf1d7654c-im-33,33,33-FF,FF,FF.gif) By dostać wielkość bezwymiarową, należy odpowiednio dobrać potęgi stałych fizycznych występujące w problemie: stałą grawitacji G oraz prędkość światła
By dostać wielkość bezwymiarową, należy odpowiednio dobrać potęgi stałych fizycznych występujące w problemie: stałą grawitacji G oraz prędkość światła  Bezwymiarowe
Bezwymiarowe 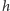 otrzymamy dla współczynnika proporcjonalności równego
otrzymamy dla współczynnika proporcjonalności równego 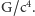 Jest to bardzo mała liczba,
Jest to bardzo mała liczba, ![−1 8,26244528 ⋅10 −45 [m −1 kg s2],](/math/temat/fizyka/grawitacja_i_wszechswiat/2017/02/26/Newtonowskie_intuicje_dla_fal_gr/9x-1bf4270b496344fba58c14f17d5cbebbf1d7654c-im-33,33,33-FF,FF,FF.gif) co oznacza, że źródłami fal o dużej amplitudzie mogą być tylko szybko poruszające się, masywne ciała. Rozważmy układ podwójny mas
co oznacza, że źródłami fal o dużej amplitudzie mogą być tylko szybko poruszające się, masywne ciała. Rozważmy układ podwójny mas 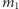 i
i 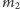 oddalonych o
oddalonych o  (separacji
(separacji 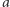 ) na orbicie kołowej. Oszacowanie
) na orbicie kołowej. Oszacowanie 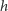 można przepisać dla takiego układu, zamieniając
można przepisać dla takiego układu, zamieniając 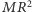 na
na 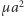 i przyjmując, że
i przyjmując, że 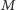 jest całkowitą, a
jest całkowitą, a 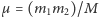 zredukowaną masą układu. Można też przyjąć, że druga pochodna
zredukowaną masą układu. Można też przyjąć, że druga pochodna 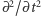 jest proporcjonalna do orbitalnej prędkości obrotowej
jest proporcjonalna do orbitalnej prędkości obrotowej 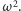 Korzystając z trzeciego prawa Keplera (patrz obok), dostaniemy
Korzystając z trzeciego prawa Keplera (patrz obok), dostaniemy
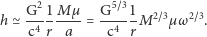 |
Dla przykładu, rząd wielkości 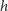 w przypadku dwóch gwiazd neutronowych o podobnych masach
w przypadku dwóch gwiazd neutronowych o podobnych masach 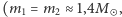
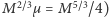 jest następujący:
jest następujący:
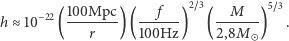 |
Charakterystyczna względna amplituda 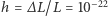 odpowiada pomiarowi odległości Słońce-Saturn z dokładnością do rozmiaru atomu! Używając argumentów newtonowskich, dostaliśmy przybliżenie kwadrupolowe amplitudy
odpowiada pomiarowi odległości Słońce-Saturn z dokładnością do rozmiaru atomu! Używając argumentów newtonowskich, dostaliśmy przybliżenie kwadrupolowe amplitudy 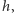 poprawne dla układów, w których prędkości nie są bliskie prędkości światła. Po raz pierwszy sformułował je w 1918 roku Albert Einstein:
poprawne dla układów, w których prędkości nie są bliskie prędkości światła. Po raz pierwszy sformułował je w 1918 roku Albert Einstein:
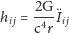 |
(dwie kropki oznaczają drugą pochodną względem czasu). Amplituda 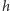 jest więc bezpośrednio związana z niesymetryczną częścią energii kinetycznej układu:
jest więc bezpośrednio związana z niesymetryczną częścią energii kinetycznej układu: 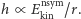
Z powyższego i notki na marginesie widać też, że 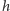 jest proporcjonalna do momentu kwadrupolowego
jest proporcjonalna do momentu kwadrupolowego 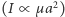 oraz
oraz 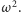 Z rozważań o strumieniu energii wiemy natomiast, że jasność układu (moc promieniowania fal)
Z rozważań o strumieniu energii wiemy natomiast, że jasność układu (moc promieniowania fal) 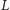 jest funkcją
jest funkcją 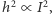 oraz
oraz 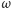 w pewnej potędze. Używając analizy wymiarowej (o której więcej napiszemy w następnym numerze), dostajemy
w pewnej potędze. Używając analizy wymiarowej (o której więcej napiszemy w następnym numerze), dostajemy
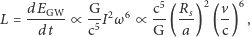 |
gdzie 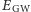 jest energią fali grawitacyjnej,
jest energią fali grawitacyjnej, 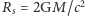 jest promieniem Schwarzschilda czarnej dziury o masie
jest promieniem Schwarzschilda czarnej dziury o masie 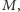 a
a 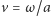 jest prędkością liniową masy
jest prędkością liniową masy 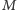 na orbicie o promieniu
na orbicie o promieniu 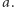 Czynnik proporcjonalności wynosi
Czynnik proporcjonalności wynosi 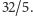 Druga wersja równania pokazuje dobitnie, że moc emitowana przez układ podwójny o rozmiarze porównywalnym z
Druga wersja równania pokazuje dobitnie, że moc emitowana przez układ podwójny o rozmiarze porównywalnym z 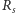 i orbitującym z prędkością bliską prędkości światła jest ogromna: czynnik
i orbitującym z prędkością bliską prędkości światła jest ogromna: czynnik 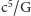 wynosi
wynosi 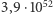 W. Dla porównania zwyczajne układy podwójne są bardzo słabymi źródłami fal. Układ Ziemia-Słońce emituje około 200 W (całkowita emisja elektromagnetyczna Słońca to około
W. Dla porównania zwyczajne układy podwójne są bardzo słabymi źródłami fal. Układ Ziemia-Słońce emituje około 200 W (całkowita emisja elektromagnetyczna Słońca to około  W).
W).
Fale emitowane są na koszt zmniejszania orbitalnej energii układu, 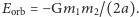 Porównanie zmiany
Porównanie zmiany 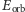 i
i 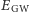 daje
daje
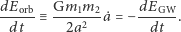 |
Używając trzeciego prawa Keplera oraz wynikającej z niego pochodnej 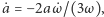 można otrzymać zależność między masami składników oraz orbitalną prędkością obrotową i jej pochodną:
można otrzymać zależność między masami składników oraz orbitalną prędkością obrotową i jej pochodną:
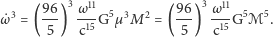 |
Kombinację mas 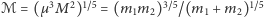 nazywa się masą ćwierku przez analogię do podobnego w charakterze zachowania się częstotliwości i amplitudy odgłosu ptaków; prędkość orbitalna oraz amplituda rośnie
nazywa się masą ćwierku przez analogię do podobnego w charakterze zachowania się częstotliwości i amplitudy odgłosu ptaków; prędkość orbitalna oraz amplituda rośnie 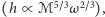 podczas gdy separacja układu
podczas gdy separacja układu 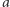 maleje. Masę ćwierku
maleje. Masę ćwierku 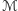 można obliczyć wprost z częstotliwości fal grawitacyjnych
można obliczyć wprost z częstotliwości fal grawitacyjnych 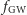 (o częstotliwości dwukrotnie większej niż orbitalna,
(o częstotliwości dwukrotnie większej niż orbitalna, 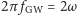 ) w detektorze:
) w detektorze:
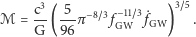 |
W połączeniu z również mierzoną bezpośrednio przez detektor amplitudą 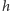 masę ćwierku można wykorzystać do obliczenia odległości do źródła:
masę ćwierku można wykorzystać do obliczenia odległości do źródła:
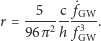 |
Metoda ta jest zupełnie niezależna od tradycyjnie używanych do tej pory przez astronomów "drabin odległości", kalibrowanych poprzez tzw. świece standardowe (np. cefeidy i supernowe typu Ia). W przyszłości pomiary odległości wieloma metodami naraz (np. jasności błysków gamma i fal grawitacyjnych przez nie emitowanych) będą porównywane dla poprawienia kosmicznej skali odległości i precyzyjnego wyznaczenia parametrów kosmologicznych, np. stałej Hubble'a.
Na koniec zastanówmy się, w jaki sposób można otrzymać masy składników dwóch dotychczas zarejestrowanych przez Advanced LIGO sygnałów, GW150914 i GW151226. Po zmierzeniu masy ćwierku ( 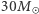 dla GW150914 i
dla GW150914 i 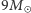 dla GW151226) do dyspozycji pozostaje nam analiza przebiegu samego ćwierku. W obu obserwacjach sygnał urywa się przy pewnej krytycznej częstości
dla GW151226) do dyspozycji pozostaje nam analiza przebiegu samego ćwierku. W obu obserwacjach sygnał urywa się przy pewnej krytycznej częstości 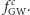 W przypadku GW
W przypadku GW 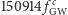 to około
to około 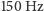 (
( 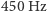 dla GW151226). Nagłe przerwanie ćwierku interpretowane jest jako zderzenie składników o skończonych rozmiarach i moment, w którym układ podwójny przestaje istnieć. Ograniczenie na rozmiar układu dostaniemy, zakładając, że składniki są czarnymi dziurami o promieniach Schwarzschilda. Zatem
dla GW151226). Nagłe przerwanie ćwierku interpretowane jest jako zderzenie składników o skończonych rozmiarach i moment, w którym układ podwójny przestaje istnieć. Ograniczenie na rozmiar układu dostaniemy, zakładając, że składniki są czarnymi dziurami o promieniach Schwarzschilda. Zatem
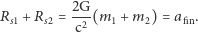 |
Krytyczną odległość 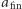 wstawiamy do trzeciego prawa Keplera, dostając oszacowanie na sumę mas
wstawiamy do trzeciego prawa Keplera, dostając oszacowanie na sumę mas
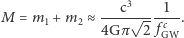 |
Dla GW150914 obliczone w ten sposób 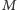 wynosi około
wynosi około 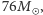 dla GW151226 dostajemy
dla GW151226 dostajemy 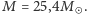 Dokładne wartości mas układu, otrzymane przy użyciu ogólnej teorii względności i symulacji numerycznych, to, odpowiednio,
Dokładne wartości mas układu, otrzymane przy użyciu ogólnej teorii względności i symulacji numerycznych, to, odpowiednio, 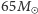 i
i 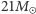 (newtonowskie oszacowanie radzi sobie zatem całkiem nieźle, jednak nie na tyle dobrze, by poprawnie określić masy składników dla obu sygnałów poprzez rozwiązanie układu równań
(newtonowskie oszacowanie radzi sobie zatem całkiem nieźle, jednak nie na tyle dobrze, by poprawnie określić masy składników dla obu sygnałów poprzez rozwiązanie układu równań 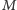 i
i 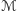 ). Alternatywną metodą jest założenie, że masy składników są podobne. Wtedy
). Alternatywną metodą jest założenie, że masy składników są podobne. Wtedy 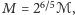 i
i 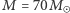 dla GW150914, oraz
dla GW150914, oraz 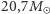 dla GW151226.
dla GW151226.
Masy końcowych czarnych dziur w obu przypadkach wynoszą 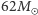 i
i 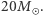 Gdzie podziała się brakująca masa? Została wyemitowana w falach grawitacyjnych. Można ją obliczyć w następujący sposób. Całkowita energia układu dla separacji
Gdzie podziała się brakująca masa? Została wyemitowana w falach grawitacyjnych. Można ją obliczyć w następujący sposób. Całkowita energia układu dla separacji 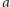 składa się z przyczynków od masy spoczynkowej i energii orbitalnej,
składa się z przyczynków od masy spoczynkowej i energii orbitalnej,
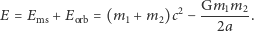 |
Zakładając dla uproszczenia, że 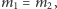 oraz że końcowa separacja
oraz że końcowa separacja 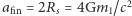 (w rzeczywistości układ staje się niestabilny dla nieco większych separacji) różnicę energii między stanem początkowym
(w rzeczywistości układ staje się niestabilny dla nieco większych separacji) różnicę energii między stanem początkowym 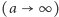 i końcowym oceniamy na
i końcowym oceniamy na 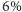 całkowitej masy-energii (
całkowitej masy-energii ( 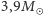 dla GW150914 i
dla GW150914 i 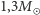 dla GW151226, w porównaniu do
dla GW151226, w porównaniu do 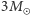 i
i 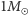 otrzymanych wyrafinowanymi metodami). Większość energii została wypromieniowana podczas przemierzania kilku ostatnich orbit oraz podczas procesu tworzenia końcowej czarnej dziury, którego nasz prosty model nie uwzględnia. W momencie największej "jasności" emitowana moc w obu przypadkach wynosiła około
otrzymanych wyrafinowanymi metodami). Większość energii została wypromieniowana podczas przemierzania kilku ostatnich orbit oraz podczas procesu tworzenia końcowej czarnej dziury, którego nasz prosty model nie uwzględnia. W momencie największej "jasności" emitowana moc w obu przypadkach wynosiła około 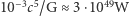 (składniki poruszały się z prędkościami mniejszymi niż prędkość światła, w odległości większej od promienia
(składniki poruszały się z prędkościami mniejszymi niż prędkość światła, w odległości większej od promienia 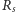 końcowej czarnej dziury). Przewyższa ona o rzędy wielkości emisję nie tylko największych dotychczas znanych kosmicznych katastrof - izotropowa emisja błysków gamma to "jedynie"
końcowej czarnej dziury). Przewyższa ona o rzędy wielkości emisję nie tylko największych dotychczas znanych kosmicznych katastrof - izotropowa emisja błysków gamma to "jedynie" 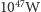 - ale także sumaryczną emisję wszystkich gwiazd we Wszechświecie. Szacowana gwiazdowa jasność obserwowanego Wszechświata, zawierającego około
- ale także sumaryczną emisję wszystkich gwiazd we Wszechświecie. Szacowana gwiazdowa jasność obserwowanego Wszechświata, zawierającego około 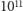 galaktyk podobnych do Drogi Mlecznej, z której każda składa się z około
galaktyk podobnych do Drogi Mlecznej, z której każda składa się z około 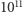 gwiazd podobnych do Słońca, wynosi bowiem około
gwiazd podobnych do Słońca, wynosi bowiem około 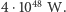
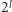 -pola to
-pola to 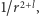 czyli już dla rozkładu monopolowego
czyli już dla rozkładu monopolowego 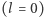 zanika zbyt szybko.
zanika zbyt szybko.![G = 6,67408 ⋅10−11 [m3 kg−1s−2]](/math/temat/fizyka/grawitacja_i_wszechswiat/2017/02/26/Newtonowskie_intuicje_dla_fal_gr/1x-39ea36f915ea25ede081bfe98f521e23352f8bca-im-33,33,33-FF,FF,FF.gif)
![|c = 299792458 [ms −1].](/math/temat/fizyka/grawitacja_i_wszechswiat/2017/02/26/Newtonowskie_intuicje_dla_fal_gr/2x-39ea36f915ea25ede081bfe98f521e23352f8bca-im-33,33,33-FF,FF,FF.gif)