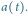Zdefiniowane obiekty umożliwiają nam obliczenie długości krzywej. Posłużę się tutaj przykładem podróży samochodem. Znając wskazanie prędkościomierza w każdej chwili, możemy obliczyć dystans, jaki pokonaliśmy. Gdy w geometrii nie mamy zdefiniowanego iloczynu skalarnego dla prędkości w każdym punkcie, to tak, jakbyśmy poruszali się samochodem, w którym prędkościomierz nie ma skali, a widzimy jedynie wychylającą się wskazówkę. Zdefiniowany obiekt 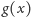pełni rolę skali, którą w każdej chwili ruchu dokładamy do tarczy. Przypominam, że jest to tylko obraz intuicyjny, a głębsze zrozumienie tych kwestii wymaga matematycznej dokładności. Możemy teraz zdefiniować odcinek „prosty”, który w ogólnym przypadku nazwiemy geodezyjną, jako krzywą, która łączy dwa punkty i ma ekstremalną długość.

Dodajmy, już bez wchodzenia w szczegóły, że obiekt 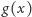pozwala przesuwać wektory „równolegle” pomiędzy punktami. Gdy dwa wektory są już zaczepione w tym samym punkcie, potrafimy je porównać. Okazuje się jednak, że przesuwając wektor wzdłuż różnych dróg, możemy otrzymać różne wyniki. Zdarza się to w sytuacji, gdy przestrzeń nie jest płaska.

Ogólna teoria wględności łączy materię z geometrią za pomocą równań Einsteina

gdzie 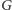jest wielkością, którą obliczamy za pomocą obiektu 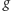i jego pochodnych, natomiast 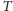jest obiektem opisującym materię. Rozwiązywanie tych równań polega na znajdowaniu 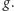Jest to zadanie dość trudne i w ogólności niewykonalne. Dlatego fizycy starają się uprościć to postępowanie, czyniąc pewne założenia na temat materii 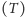lub na temat symetrii czasoprzestrzeni, co ma swoje odzwierciedlenie w postaci

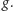
Rozważając czasoprzestrzeń całkowicie pozbawioną materii 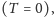która jest sferycznie symetryczna, otrzymujemy rozwiązanie opisujące czarną dziurę. Ciekawe, że rozwiązanie takie ma jeden wolny parametr, który okazuje się być masą w rozumieniu grawitacji Newtona. Analogię tę znajdujemy, badając ruch cząstek próbnych daleko od centrum symetrii. Poruszają się one tak, jak gdyby znajdowały się w newtonowskim polu grawitacyjnym masy 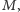mimo iż, jak wspomniałem na początku, rozważaliśmy pustą czasoprzestrzeń. Rowiązanie to ma również tę własność, że środek symetrii jest punktem, który fizycy nazywają osobliwością – miejscem, gdzie teoria się załamuje, gdyż pewne własności geometrii stają się tak ekstremalne, a opisujące geometrię parametry nieskończone, że przestajemy wierzyć w możliwość istnienia takich warunków w przyrodzie (matematycy zdają się zachowywać zimną krew w obliczu takich nieskończoności).

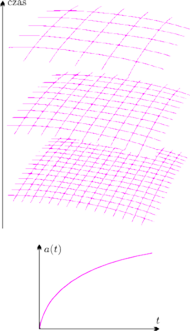
Rys. 3. W rozszerzającym się Wszechświecie przestrzeń ,,puchnie". Wzrost odległości między ustalonymi punktami-galaktykami opisuje funkcja

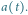
Rozważając innymodel,w którym Wszechświat wypełniony jest pyłem – za ziarenka tego pyłu służą galaktyki! – otrzymujemy modele kosmologiczne. Dodatkowo czynimy założenie, uzasadnione doświadczalnie, że Wszechświat jest jednorodny i izotropowy. Oznacza to tylko tyle, że wygląda on tak samo, bez względu na to, w którym kierunku i z którego miejsca go obserwujemy. 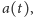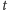Założenia te okazują się na tyle silne, że pozwalają sprowadzić ewolucjęWszechświata do badania jednej funkcji gdzie jest współrzędnościowym czasem Wszechświata. Czasoprzestrzeń modelu kosmologicznegomożemy pociąć na trójwymiarowe plastry, które następują po sobie. O kolejności ich następowania mówi parametr 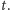Wszystkie plastry są takie same i mogą być nieskończone. Liczba 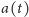mówi nam o tym, jak zmienia się skala tych plastrów. Na przykład, w tzw. modelu płaskim poszczególne plastry są trójwymiarowymi przestrzeniami euklidesowymi. Gdy zaznaczymy dowolne dwa punkty (tj. odległe galaktyki), to ich fizyczna odległość będzie zmieniała się zgodnie ze wzorem 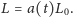Model kosmologiczny przewiduje, że dla odpowiednio małego parametru czynnik skali wyniesie i cały nieskończony plaster zostanie ściśnięty tak, że odległość dowolnych dwóch punktów wyniesie zero – i gęstość Wszechświata będzie nieskończona. Podobnie jak w przypadku sferycznie symetrycznym jest to punkt, w którym załamuje się teoria. Tę osobliwość nazywamy popularnie Wielkim Wybuchem, choć dziś miano to zarezerwowano raczej dla procesu, w którym wyłonił się gorący, wypełniony promieniowaniem Wszechświat.

Istnienie tych dziwnych punktów sprawia, że fizycy obdarzają teorię małym zaufaniem w ich otoczeniu. Wierzą, że tak jak dla materii, gdzie teoria kwantowa rozwiązała wiele problemów z niepożądanymi nieskończonościami, odpowiednia kwantowa teoria grawitacji i geometrii zapewni rozwiązanie problemu osobliwości. Jednak, choć wielu fizyków głowi się nieustannie nad sformułowaniem takiej teorii, jak dotąd ostateczna odpowiedź wymyka się umysłom badaczy, tworzących konkurencyjne modele. Jeden z takich modeli – pętlowa kwantowa grawitacja – pozwala przeformułować ogólną teorięwzględnościwsposób, który czyni ją podobną kwantowym teoriom opisującym materię. Postępując analogicznie jak w tamtych przypadkach, otrzymujemy nowy model kosmologiczny, w którym nie występuje początkowa osobliwość Wszechświata. W modelu tym Wszechświat dawno temu kurczył się, osiągając stan o maksymalnej gęstości, po czym zaczął się rozszerzać i rozszerzanie to trwa po dziś dzień.

Czy jest to dobry opis? Tego zagwarantować nie można, model wymaga bowiem wciąż wiele pracy dla jego lepszego zrozumienia. Być może jednak jesteśmy świadkami wyłaniania się odpowiedzi na trapiący od dawna fizyków problem początkowej osobliwości...

Przedstawiony tutaj obraz jest, oczywiście, bardzo uproszczony i niepełny. Czytelnika Wnikliwego, który chciałby dowiedzieć się czegoś więcej o grawitacji i geometrii, odsyłam do podanej poniżej literatury.