Co to jest?
Grawitacja i geometria – szybki przegląd
Ogólna teoria względności nauczyła nas, że geometria jest nieodłączną częścią współczesnej fizyki. W teorii tej Albert Einstein wskazał geometrii miejsce równoważne temu, które zajmuje materia. Sprawił, że ta pierwsza stała się obiektem dynamicznym i zaczęto pytać o jej ewolucję i kształt.
Rys. 1.
Wymagało to stworzenia nowego, geometrycznego języka, którym dziś posługuje się współczesna fizyka. Mimo iż ogólna teoria względności jest dość dobrze spopularyzowana, podobnie jak wynikająca z niej współczesna kosmologia, to jej geometryczny opis jest mniej znany szerokim rzeszom czytelników. W niniejszym artykule postaram się uzupełnić tę lukę.
Zacznijmy od nauczanej w szkole fizyki, która odwołuje się do pojęć wprowadzonych jeszcze przez Izaaka Newtona. Uprawiając fizykę newtonowską, mamy do dyspozycji z góry zadaną geometrię. Absolutna przestrzeń jest przestrzenią euklidesową, z którą zapoznajemy się już na początku szkoły podstawowej. Dodatkowo dysponujemy absolutnym czasem, który jest od przestrzeni niezależny i płynie jednostajnie własnym torem.

Rys. 2. W małym otoczeniu punktów możemy geometrię zakrzywionej przestrzeni przybliżać geometrią euklidesową.
Przestrzeń euklidesową możemy modelować za pomocą iloczynu
kartezjańskiego trzech kopii zbioru liczb rzeczywistych, tj.
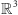 . Punkty
takiej przestrzeni to uporządkowane trójki liczb
. Punkty
takiej przestrzeni to uporządkowane trójki liczb
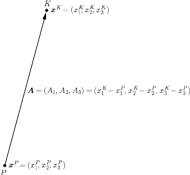
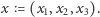 Podstawowymi obiektami są wektory przesunięcia, a więc wektory, które
możemy sobie wyobrazić jako strzałki łączące dwa dane punkty, z których
jeden jest punktem początkowym, a drugi końcowym.
Podstawowymi obiektami są wektory przesunięcia, a więc wektory, które
możemy sobie wyobrazić jako strzałki łączące dwa dane punkty, z których
jeden jest punktem początkowym, a drugi końcowym.
W przestrzeni euklidesowej możemy porównywać dwa wektory, bez względu na to, jakie punkty je wyznaczają. Pomaga nam w tym piąty aksjomat Euklidesa, który mówi o tym, że na płaszczyźnie przez punkt poza prostą można poprowadzić dokładnie jedną prostą z nią rozłączną. Mamy zdefiniowany iloczyn skalarny

który pozwala obliczać długości wektorów i kąt pomiędzy nimi. Za pomocą tego iloczynu możemy wyznaczać długość dowolnej krzywej. Możemy też zdefiniować odcinek „prosty” jako krzywą o minimalnej długości łączącą dane dwa punkty.
W przypadku dowolnych przestrzeni powyższe podejście może nie być słuszne. Po pierwsze, piąty aksjomat Euklidesa może nie być spełniony. Po drugie, dwa punkty nie muszą wyznaczać wektora. Po trzecie, nie możemy porównywać wektorów zaczepionych w różnych punktach. Geometria może być euklidesowa tylko w małej skali, tzn. w otoczeniu dowolnego punktu możemy ją za taką uważać, o ile nie oddalamy się za daleko.
Musimy poradzić sobie jeszcze z problemem absolutnego czasu. Czas musi stać się nieodłączną częścią geometrii, która stanie się geometrią czasoprzestrzeni, a nie tylko przestrzeni. Aby poradzić sobie z tymi problemami, fizycy potrzebowali nowego aparatu matematycznego – stworzonej przez Riemanna geometrii różniczkowej. Podstawowymi, używanymi przez nich obiektami, są:
- 1)
- Pewien zbiór, który nazywamy rozmaitością. Ma on tę własność,
że
lokalnie, w odpowiednio małym otoczeniu każdego punktu, wygląda on
jak
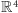 . Sprawia to, że otoczenie każdego punktu możemy w
pewien niejednoznaczny sposób utożsamić z podzbiorem
. Sprawia to, że otoczenie każdego punktu możemy w
pewien niejednoznaczny sposób utożsamić z podzbiorem
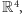 ale nie możemy tego zrobić globalnie. Jest to sytuacja podobna do
tej, z jaką mamy do czynienia, żyjąc na powierzchni Ziemi. Poruszając
się w swoim mieście, nie jesteśmy w stanie poczuć jej kulistości,
a nasze otoczenie wydaje się płaskie. Mapę naszego miasta możemy
narysować z doskonałą dokładnością na płaskiej kartce papieru, a dane
miejsce może znajdować się na kilku różnych mapach spośród
wielu pokrywających glob.
ale nie możemy tego zrobić globalnie. Jest to sytuacja podobna do
tej, z jaką mamy do czynienia, żyjąc na powierzchni Ziemi. Poruszając
się w swoim mieście, nie jesteśmy w stanie poczuć jej kulistości,
a nasze otoczenie wydaje się płaskie. Mapę naszego miasta możemy
narysować z doskonałą dokładnością na płaskiej kartce papieru, a dane
miejsce może znajdować się na kilku różnych mapach spośród
wielu pokrywających glob.
- 2)
- W każdym punkcie naszej przestrzeni mamy zaczepioną pewną przestrzeń ,,wszystkich możliwych prędkości”, jakie może mieć ciało, poruszając się po krzywej przechodzącej przez ten punkt. Wyrażenia w cudzysłowie nie należy rozumieć zbyt dosłownie. Ma ono na celu wywołać pewne skojarzenie i pobudzić intuicję. Przypominam jednak, że nie mamy już absolutnego czasu i ścisła definicja wymaga matematycznej staranności. W odróżnieniu od przypadku przestrzeni euklidesowej nie możemy porównywać ,,prędkośc” w różnych punktach.
- 3)
- W każdym punkcie z osobna mamy iloczyn skalarny dla wektorów
,,prędkości” zdefiniowanych powyżej. Będziemy go oznaczali przez
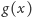 , gdzie
, gdzie
 przypomina nam o tym, że wielkość ta
zależy od punktu. Pozwala nam on obliczyć długości prędkości i kąt
pomiędzy nimi, ale tylko w danym punkcie.
przypomina nam o tym, że wielkość ta
zależy od punktu. Pozwala nam on obliczyć długości prędkości i kąt
pomiędzy nimi, ale tylko w danym punkcie.