Zadania z matematyki - IX 2020»Zadanie 1650
o zadaniu...
- Zadanie pochodzi z artykułu Zadania z matematyki - IX 2020
- Publikacja w Delcie: wrzesień 2020
- Publikacja elektroniczna: 31 sierpnia 2020
Na tablicy zapisanych jest 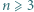 różnych liczb rzeczywistych, przy czym
różnych liczb rzeczywistych, przy czym  jest liczbą nieparzystą. Dla każdej pary
jest liczbą nieparzystą. Dla każdej pary 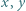 liczb z tablicy na osobnej karteczce zapisano liczbę
liczb z tablicy na osobnej karteczce zapisano liczbę 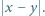 Wykazać, że wszystkie karteczki można podzielić na dwa stosy o równych sumach zapisanych liczb.
Wykazać, że wszystkie karteczki można podzielić na dwa stosy o równych sumach zapisanych liczb.
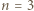 niech
niech 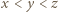 będą elementami zbioru
będą elementami zbioru 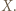 Wówczas na jednym stosie kładziemy karteczkę z liczbą
Wówczas na jednym stosie kładziemy karteczkę z liczbą 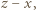 a na drugim - karteczki z liczbami
a na drugim - karteczki z liczbami 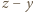 oraz
oraz 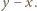
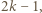 i rozważmy dowolny zbiór
i rozważmy dowolny zbiór 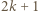 liczb
liczb 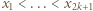 oraz związane z nimi karteczki. Z założenia indukcyjnego wszystkie karteczki pochodzące wyłącznie od liczb
oraz związane z nimi karteczki. Z założenia indukcyjnego wszystkie karteczki pochodzące wyłącznie od liczb 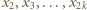 można podzielić na stosy o równych sumach. Pozostałe karteczki najpierw podzielmy na następujące
można podzielić na stosy o równych sumach. Pozostałe karteczki najpierw podzielmy na następujące 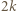 grup:
grup: 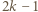 grup po dwie karteczki, z liczbami
grup po dwie karteczki, z liczbami 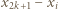 oraz
oraz 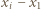 dla
dla 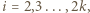 oraz jedna grupa składająca się z pozostałej karteczki z liczbą
oraz jedna grupa składająca się z pozostałej karteczki z liczbą 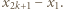 Zauważmy, że w każdej grupie suma liczb z karteczek jest równa
Zauważmy, że w każdej grupie suma liczb z karteczek jest równa 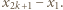 Wobec tego wystarczy karteczki z dowolnych
Wobec tego wystarczy karteczki z dowolnych 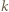 grup dołączyć do jednego stosu, a karteczki z pozostałych
grup dołączyć do jednego stosu, a karteczki z pozostałych 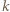 grup - do drugiego stosu. To kończy dowód indukcyjny.
grup - do drugiego stosu. To kończy dowód indukcyjny.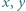 liczb z tablicy na osobnej karteczce zapisano liczbę
liczb z tablicy na osobnej karteczce zapisano liczbę 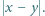 Czy może się zdarzyć, że na karteczkach zapisano liczby całkowite od 1 do 10?
Czy może się zdarzyć, że na karteczkach zapisano liczby całkowite od 1 do 10?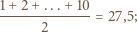
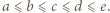 Wówczas najmniejsza z liczb zapisanych na karteczkach to
Wówczas najmniejsza z liczb zapisanych na karteczkach to 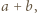 druga najmniejsza (być może równa) -
druga najmniejsza (być może równa) - 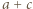 ; największa to
; największa to  a druga największa -
a druga największa - 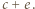 Ponadto sumując liczby ze wszystkich karteczek, uzyskujemy
Ponadto sumując liczby ze wszystkich karteczek, uzyskujemy 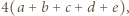 a zatem znamy również wartość
a zatem znamy również wartość 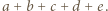 Ta wiedza wystarcza kolejno do znalezienia wartości
Ta wiedza wystarcza kolejno do znalezienia wartości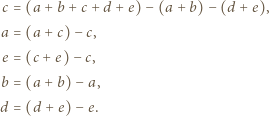
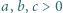 spełniają warunek
spełniają warunek 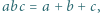 to
to 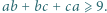
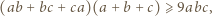
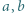 i
i  spełniają równość
spełniają równość 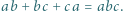 Dowieść, że
Dowieść, że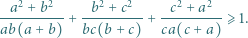
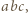 a prawą przez
a prawą przez 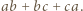 Następnie skorzystać z nierówności
Następnie skorzystać z nierówności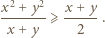
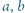 i
i  spełniają warunek
spełniają warunek 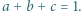 Dowieść, że
Dowieść, że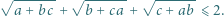
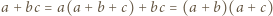 wraz z dwiema analogicznymi równościami. Wykorzystać nierówność
wraz z dwiema analogicznymi równościami. Wykorzystać nierówność 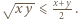
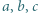 jest równy 1, to
jest równy 1, to 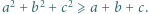
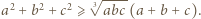 Można to zrobić, dodając stronami nierówność między średnią arytmetyczną i geometryczną
Można to zrobić, dodając stronami nierówność między średnią arytmetyczną i geometryczną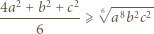
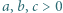 prawdziwa jest nierówność
prawdziwa jest nierówność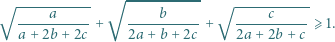
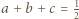 i udowodnić, że
i udowodnić, że 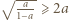 dla
dla 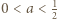 oraz analogicznie dla
oraz analogicznie dla 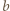 i
i 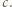
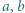 i
i  oraz liczby całkowitej
oraz liczby całkowitej 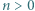 zachodzi nierówność
zachodzi nierówność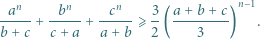
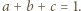 Wtedy
Wtedy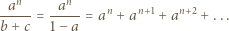
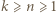 z nierówności
z nierówności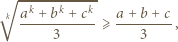
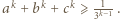 Tę ostatnią nierówność wystarczy zsumować dla
Tę ostatnią nierówność wystarczy zsumować dla 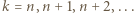
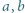 i
i  oraz liczby całkowitej
oraz liczby całkowitej 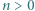 zachodzi nierówność
zachodzi nierówność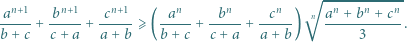
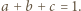 Posługując się nierównościami między średnimi potęgowymi, wykazać dla
Posługując się nierównościami między średnimi potęgowymi, wykazać dla 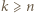 nierówności
nierówności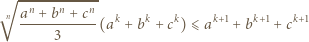
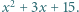 Następnie wszyscy uczniowie w klasie podchodzili kolejno do tablicy; każdy z nich zmniejszał albo zwiększał o jeden współczynnik przy
Następnie wszyscy uczniowie w klasie podchodzili kolejno do tablicy; każdy z nich zmniejszał albo zwiększał o jeden współczynnik przy  albo wyraz wolny trójmianu. Na koniec okazało się, że na tablicy widnieje trójmian
albo wyraz wolny trójmianu. Na koniec okazało się, że na tablicy widnieje trójmian 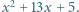 Udowodnić, że w pewnym momencie na tablicy był napisany trójmian o pierwiastkach całkowitych.
Udowodnić, że w pewnym momencie na tablicy był napisany trójmian o pierwiastkach całkowitych.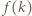 będzie wartością danego trójmianu w punkcie
będzie wartością danego trójmianu w punkcie 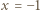 po zmianie współczynników przez
po zmianie współczynników przez 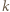 -tego ucznia i niech
-tego ucznia i niech 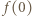 będzie wartością w -1 trójmianu napisanego przez nauczyciela. Zauważmy, że
będzie wartością w -1 trójmianu napisanego przez nauczyciela. Zauważmy, że 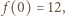 a
a 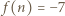 (gdzie
(gdzie 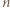 to numer ostatniego ucznia). Ponadto zachodzi nierówność
to numer ostatniego ucznia). Ponadto zachodzi nierówność 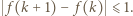 Rzeczywiście - jest to jasne, gdy zmieniamy wyraz wolny, zaś zmieniając o
Rzeczywiście - jest to jasne, gdy zmieniamy wyraz wolny, zaś zmieniając o 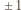 wartość współczynnika przy
wartość współczynnika przy 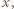 dodajemy lub odejmujemy 1 do wartości wielomianu w -1. W takim razie istnieje takie
dodajemy lub odejmujemy 1 do wartości wielomianu w -1. W takim razie istnieje takie 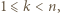 że
że 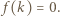 Zatem w pewnym momencie na tablicy był napisany trójmian
Zatem w pewnym momencie na tablicy był napisany trójmian 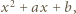 którego jednym z pierwiastków było -1; ze wzorów Viète'a wnosimy, że drugim jego pierwiastkiem była liczba całkowita
którego jednym z pierwiastków było -1; ze wzorów Viète'a wnosimy, że drugim jego pierwiastkiem była liczba całkowita 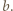
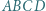 zachodzi równość
zachodzi równość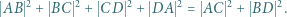
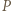 będzie punktem przecięcia przekątnych równoległoboku. Wyznaczyć
będzie punktem przecięcia przekątnych równoległoboku. Wyznaczyć 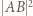 z twierdzenia cosinusów dla trójkąta
z twierdzenia cosinusów dla trójkąta 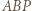 , podobnie trzy pozostałe kwadraty długości boków.
, podobnie trzy pozostałe kwadraty długości boków.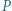 leży na boku
leży na boku 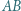 trójkąta
trójkąta 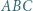 . Niech
. Niech 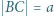 ,
, 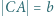 ,
, 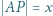 i
i 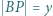 . Dowieść, że
. Dowieść, że 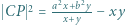 (twierdzenie Stewarta).
(twierdzenie Stewarta).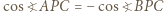 . Wyznaczyć lewą i prawą stronę z twierdzenia cosinusów dla trójkątów odpowiednio
. Wyznaczyć lewą i prawą stronę z twierdzenia cosinusów dla trójkątów odpowiednio 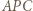 i
i 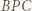 , a następnie przekształcić otrzymaną równość, by otrzymać
, a następnie przekształcić otrzymaną równość, by otrzymać 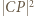 .
.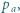
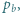
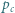 i
i 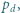 mające wspólny początek
mające wspólny początek 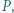 które zostały podane w kolejności antyzegarowej. Prosta
które zostały podane w kolejności antyzegarowej. Prosta 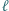 przecina je odpowiednio w punktach
przecina je odpowiednio w punktach 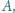
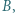
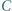 i
i 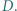 Dowieść, że wartość wyrażenia
Dowieść, że wartość wyrażenia 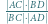 nie zależy od wyboru prostej
nie zależy od wyboru prostej 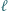 (niezmienniczość dwustosunku).
(niezmienniczość dwustosunku).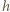 będzie odległością punktu
będzie odległością punktu 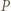 od prostej
od prostej 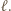 Oznaczmy przez
Oznaczmy przez 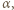
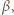
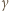 kąty pomiędzy półprostymi odpowiednio
kąty pomiędzy półprostymi odpowiednio 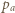 i
i 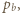
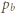 i
i 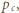
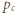 i
i 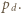 Wówczas obliczając na dwa sposoby pole trójkąta
Wówczas obliczając na dwa sposoby pole trójkąta 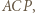 otrzymamy
otrzymamy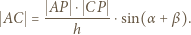
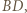
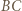 i
i 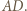
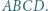 Punkty
Punkty 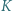 i
i 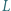 leżą odpowiednio na odcinkach
leżą odpowiednio na odcinkach 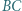 i
i 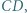 przy czym trójkąt
przy czym trójkąt 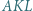 jest równoboczny. Dowieść, że suma pól trójkątów
jest równoboczny. Dowieść, że suma pól trójkątów 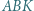 i
i 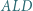 jest równa polu trójkąta
jest równa polu trójkąta 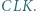
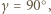 to
to ![1 [ABC] = 4 c2sin2α .](/math/temat/matematyka/geometria/zadania/2020/01/29/zm-20-02-kpo-4/2x-d78da09147956ae846d84f71c06c7431235d18c7-im-66,57,43-FF,FF,FF.gif) Niech
Niech 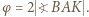 Zadanie sprowadza się do wykazania równości
Zadanie sprowadza się do wykazania równości 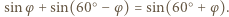
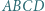 wpisany jest w okrąg. Na tym okręgu leży punkt
wpisany jest w okrąg. Na tym okręgu leży punkt 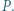 Udowodnić, że iloczyn odległości punktu
Udowodnić, że iloczyn odległości punktu 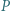 od prostych
od prostych 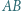 i
i 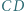 jest równy iloczynowi odległości punktu
jest równy iloczynowi odległości punktu 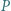 od prostych
od prostych 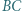 i
i 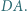
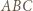 opuszczona z wierzchołka
opuszczona z wierzchołka 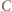 ma długość
ma długość 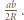 Odległości punktu
Odległości punktu 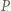 od prostych
od prostych 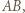
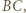
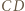 i
i 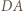 są odpowiednio wysokościami trójkątów
są odpowiednio wysokościami trójkątów 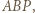
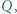
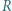 leżą odpowiednio na bokach
leżą odpowiednio na bokach 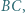
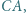
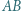 trójkąta
trójkąta 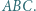 Spełnione są następujące równości:
Spełnione są następujące równości:
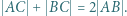
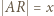 i
i 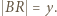 Obliczając pole trójkąta
Obliczając pole trójkąta 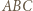 na dwa sposoby, otrzymamy równość
na dwa sposoby, otrzymamy równość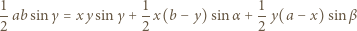
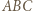 i uprościć tę równość.
i uprościć tę równość.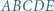 zachodzą następujące równości:
zachodzą następujące równości: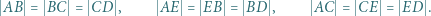
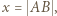
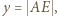
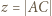 oraz
oraz 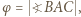
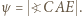 Z równości
Z równości 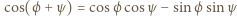 otrzymamy po przekształceniach
otrzymamy po przekształceniach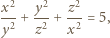
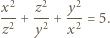
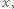
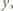
 są równe, a dzięki założeniu o wypukłości pięciokąta mamy
są równe, a dzięki założeniu o wypukłości pięciokąta mamy 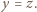 Dalszą część rozwiązania stanowią proste rachunki na kątach.
Dalszą część rozwiązania stanowią proste rachunki na kątach.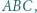 wpisanym w okrąg o środku
wpisanym w okrąg o środku 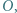 kąt przy wierzchołku
kąt przy wierzchołku 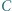 jest rozwarty oraz zachodzi równość
jest rozwarty oraz zachodzi równość 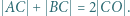 Odcinki
Odcinki 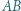 i
i 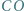 przecinają się w punkcie
przecinają się w punkcie 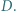 Dwusieczne kątów
Dwusieczne kątów 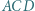 i
i 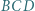 przecinają odcinek
przecinają odcinek 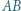 w punktach odpowiednio
w punktach odpowiednio 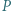 i
i 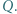 Dowieść, że punkt
Dowieść, że punkt 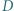 jest środkiem odcinka
jest środkiem odcinka 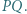
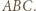 Z twierdzenia o dwusiecznej zastosowanego dla trójkąta
Z twierdzenia o dwusiecznej zastosowanego dla trójkąta 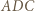 otrzymujemy
otrzymujemy 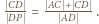 Miary kątów trójkąta
Miary kątów trójkąta 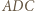 wynoszą odpowiednio
wynoszą odpowiednio 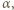
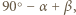
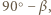 więc z twierdzenia sinusów
więc z twierdzenia sinusów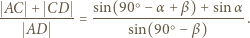
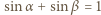 (treść zadania + twierdzenie sinusów), otrzymamy
(treść zadania + twierdzenie sinusów), otrzymamy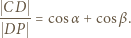
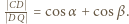
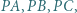 gdzie
gdzie 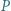 jest punktem wewnątrz trójkąta równobocznego
jest punktem wewnątrz trójkąta równobocznego 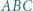 o boku 1.
o boku 1.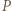 poprowadźmy proste równoległe do boków trójkąta
poprowadźmy proste równoległe do boków trójkąta 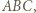 przecinające te boki w punktach
przecinające te boki w punktach 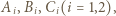 jak na rysunku. Wówczas
jak na rysunku. Wówczas 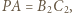 podobnie z długościami
podobnie z długościami 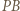 i
i 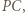 stąd należy zmaksymalizować pole trójkąta
stąd należy zmaksymalizować pole trójkąta 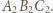 Oznaczając przez
Oznaczając przez ![[ |ℱ]](/math/temat/matematyka/geometria/planimetria/zadania/2019/12/31/zm-1626/8x-41db305196f42d3571e63f038f06f6638fa3e307-im-66,57,43-FF,FF,FF.gif) pole figury
pole figury 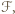 dostajemy
dostajemy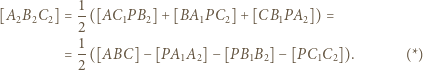
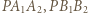 i
i 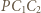 są podobne do
są podobne do 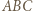 w skalach odpowiednio
w skalach odpowiednio 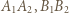 i
i 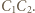 W związku z tym
W związku z tym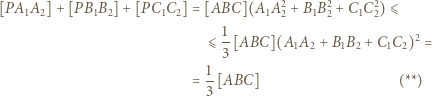
![|[A2B2C2]](/math/temat/matematyka/geometria/planimetria/zadania/2019/12/31/zm-1626/17x-41db305196f42d3571e63f038f06f6638fa3e307-im-66,57,43-FF,FF,FF.gif) Równość otrzymamy, biorąc za punkt
Równość otrzymamy, biorąc za punkt 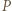 środek ciężkości trójkąta
środek ciężkości trójkąta 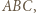 co kończy rozwiązanie.
co kończy rozwiązanie.