Nigdy Cię nie zobaczę?
- Hop, hop, jest tam kto? - krzyczy 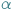 otoczona tłumem.
otoczona tłumem.
- Hop, hop, spójrz tutaj. - odpowiada 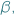 który co prawda słyszy
który co prawda słyszy 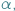 ale zupełnie jej nie widzi.
ale zupełnie jej nie widzi.
- Jakie "tutaj"? Przecież dookoła nie ma żywej duszy. - 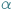 otoczona tłumem po raz kolejny usiłuje dostrzec
otoczona tłumem po raz kolejny usiłuje dostrzec 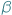 pośród otaczającej pustki.
pośród otaczającej pustki.
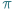 - jej rozwinięcie dziesiętne miałoby skrywać wszelkie tajemnice tego świata i odpowiedzi na wszystkie fundamentalne dla ludzkości pytania.
- jej rozwinięcie dziesiętne miałoby skrywać wszelkie tajemnice tego świata i odpowiedzi na wszystkie fundamentalne dla ludzkości pytania.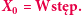 W roku 2009 słowem dziesięciolecia stowarzyszenie American Dialect Society ogłosiło czasownik to google, którego polski odpowiednik - guglować/guglać - omawiany jest już na stronach Słownika Języka Polskiego, PWN. Nic dziwnego, wszak korzystanie z wyszukiwarki Google stało się elementem codzienności większości z nas i nie mamy skrupułów przed zadawaniem jej pytań o najbłahsze sprawy. Idąc za myślą przewodnią tego numeru Delty, o nieoczekiwanych związkach teorii z rzeczywistością, pokażemy, co wspólnego ma wszędobylska wyszukiwarka z teorią łańcuchów Markowa, sformułowaną w początkach XX wieku.
W roku 2009 słowem dziesięciolecia stowarzyszenie American Dialect Society ogłosiło czasownik to google, którego polski odpowiednik - guglować/guglać - omawiany jest już na stronach Słownika Języka Polskiego, PWN. Nic dziwnego, wszak korzystanie z wyszukiwarki Google stało się elementem codzienności większości z nas i nie mamy skrupułów przed zadawaniem jej pytań o najbłahsze sprawy. Idąc za myślą przewodnią tego numeru Delty, o nieoczekiwanych związkach teorii z rzeczywistością, pokażemy, co wspólnego ma wszędobylska wyszukiwarka z teorią łańcuchów Markowa, sformułowaną w początkach XX wieku.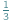 ?
?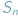 do liczby rzutów
do liczby rzutów 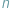 nie będzie się wiele różnił od
nie będzie się wiele różnił od 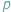 - prawdopodobieństwa otrzymania orła w pojedynczym rzucie.
- prawdopodobieństwa otrzymania orła w pojedynczym rzucie.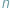 razy.
razy. ryb, ale liczby
ryb, ale liczby  nie znamy. Chcielibyśmy tę liczbę oszacować, nie uciekając się do osuszenia jeziora. Powiedzmy, że dysponujemy wędką, puszką farby i odrobiną wiedzy ze statystyki. Łowimy sobie jedną rybkę po drugiej i wrzucamy z powrotem do jeziora, krzywdy żadnej rybce nie czyniąc. Przed wrzuceniem do wody malujemy rybce kreseczkę na ogonku...
nie znamy. Chcielibyśmy tę liczbę oszacować, nie uciekając się do osuszenia jeziora. Powiedzmy, że dysponujemy wędką, puszką farby i odrobiną wiedzy ze statystyki. Łowimy sobie jedną rybkę po drugiej i wrzucamy z powrotem do jeziora, krzywdy żadnej rybce nie czyniąc. Przed wrzuceniem do wody malujemy rybce kreseczkę na ogonku...