Trysekcja kąta w "Geometrii" Kartezjusza»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu Trysekcja kąta w "Geometrii" Kartezjusza
- Publikacja w Delcie: listopad 2020
- Publikacja elektroniczna: 1 listopada 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (514 KB)
Podzielić dany kąt na trzy równe części.
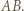 Okrąg o średnicy
Okrąg o średnicy 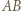 przecina proste
przecina proste 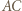 i
i 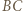 w punktach, które są spodkami wysokości trójkąta
w punktach, które są spodkami wysokości trójkąta 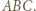

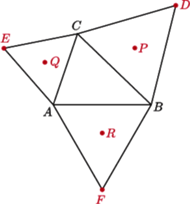
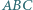 zbudowano, na zewnątrz, trójkąty równoboczne
zbudowano, na zewnątrz, trójkąty równoboczne 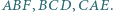 Skonstruuj trójkąt
Skonstruuj trójkąt 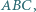 mając dane tylko punkty
mając dane tylko punkty 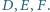
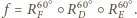 Na mocy
Na mocy 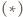 jest to obrót o
jest to obrót o 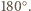 Skoro
Skoro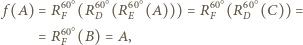
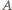 jest punktem stałym (środkiem) tego obrotu, czyli
jest punktem stałym (środkiem) tego obrotu, czyli 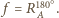
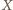 i wyznaczmy
i wyznaczmy 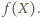 Wówczas otrzymujemy kolejno:
Wówczas otrzymujemy kolejno: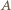 jako środek odcinka o końcach
jako środek odcinka o końcach 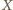 i
i 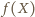 ,
, 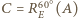 oraz
oraz 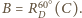
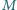 leżący we wnętrzu kąta o wierzchołku
leżący we wnętrzu kąta o wierzchołku 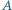 poprowadzić prostą, która, przecinając ramiona kąta w punktach
poprowadzić prostą, która, przecinając ramiona kąta w punktach 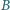 i
i 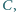 wyznacza trójkąt
wyznacza trójkąt 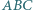 o najmniejszym polu.
o najmniejszym polu.

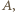 a jego przekątne przecinają się w punkcie
a jego przekątne przecinają się w punkcie 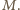 Przekątna tego równoległoboku, która przecina ramiona kąta (w punktach
Przekątna tego równoległoboku, która przecina ramiona kąta (w punktach 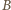 i
i 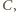
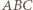 o najmniejszym polu.
o najmniejszym polu.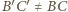 jest inną prostą przechodzącą przez punkt
jest inną prostą przechodzącą przez punkt 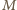 (na przykład taką, że
(na przykład taką, że 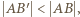
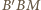 i
i 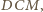 mamy:
mamy: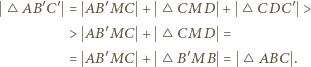
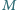 leżący we wnętrzu kąta o wierzchołku
leżący we wnętrzu kąta o wierzchołku 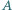 poprowadzić prostą, która, przecinając ramiona kąta w punktach
poprowadzić prostą, która, przecinając ramiona kąta w punktach 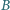 i
i 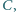 wyznacza trójkąt
wyznacza trójkąt 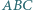 o najmniejszym obwodzie.
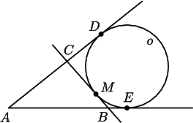
o najmniejszym obwodzie.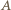 wpisujemy dwa okręgi przechodzące przez punkt
wpisujemy dwa okręgi przechodzące przez punkt 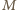 (
(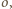 w punkcie
w punkcie 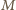 wyznaczamy styczną, która przecina ramiona kąta w punktach
wyznaczamy styczną, która przecina ramiona kąta w punktach 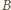 i
i 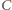 (
(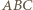 spełnia warunki zadania i ma najmniejszy obwód równy
spełnia warunki zadania i ma najmniejszy obwód równy 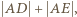 gdzie
gdzie 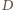 i
i 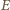 to punkty styczności okręgu
to punkty styczności okręgu  z ramionami kąta (jest tak, bo
z ramionami kąta (jest tak, bo 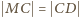 i
i 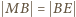 ).
).
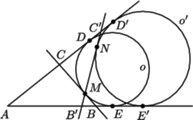
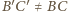 jest inną prostą zawierającą punkt
jest inną prostą zawierającą punkt 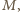 to okrąg
to okrąg 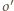 dopisany do trójkąta
dopisany do trójkąta 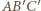 jest styczny do ramion kąta w punktach
jest styczny do ramion kąta w punktach 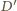 i
i 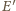 oraz do odcinka
oraz do odcinka 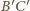 w punkcie
w punkcie 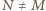 (
(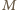 leży na zewnątrz okręgu dopisanego
leży na zewnątrz okręgu dopisanego 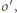 więc okrąg
więc okrąg 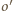 ma większy promień niż okrąg
ma większy promień niż okrąg  i obwód trójkąta
i obwód trójkąta 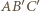 jest równy
jest równy